- Research Article
- Open access
- Published:
Blow up of the Solutions of Nonlinear Wave Equation
Boundary Value Problems volume 2007, Article number: 042954 (2007)
Abstract
We construct for every fixed the metric
the metric , where
, where ,
, ,
, ,
, , are continuous functions,
, are continuous functions, , for which we consider the Cauchy problem
, for which we consider the Cauchy problem , where
, where ,
, ;
; ,
, , where
, where ,
, ,
, ,
, ,
, ,
, ,
, and
and are positive constants. When
are positive constants. When , we prove that the above Cauchy problem has a nontrivial solution
, we prove that the above Cauchy problem has a nontrivial solution in the form
in the form for which
for which . When
. When , we prove that the above Cauchy problem has a nontrivial solution
, we prove that the above Cauchy problem has a nontrivial solution in the form
in the form for which
for which .
.
References
Jörgens K: Das Anfangswertproblem im Grossen für eine Klasse nichtlinearer Wellengleichungen. Mathematische Zeitschrift 1961, 77: 295–308. 10.1007/BF01180181
Shatah J, Struwe M: Geometric Wave Equations, Courant Lecture Notes in Mathematics. Volume 2. New York University, Courant Institute of Mathematical Sciences, New York, NY, USA; 1998:viii+153.
Rauch J: The
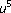 -Klein-Gordon equation. II. Anomalous singularities for semilinear wave equations. In Nonlinear Partial Differential Equations and Their Applications. Collège de France Seminar, Vol. I, Research Notes in Math. Volume 53. Edited by: Breizis H, Lions JL. Pitman, Boston, Mass, USA; 1981:335–364.
-Klein-Gordon equation. II. Anomalous singularities for semilinear wave equations. In Nonlinear Partial Differential Equations and Their Applications. Collège de France Seminar, Vol. I, Research Notes in Math. Volume 53. Edited by: Breizis H, Lions JL. Pitman, Boston, Mass, USA; 1981:335–364.Georgiev SG: Blow up of solutions for Klein-Gordon equations in the Reissner-Nordström metric. Electronic Journal of Differential Equations 2005,2005(67):1–22.
John F: Blow-up of solutions of nonlinear wave equations in three space dimensions. Manuscripta Mathematica 1979,28(1–3):235–268.
Georgiev SG: Blow up of the solutions of nonlinear wave equation in Reissner-Nordström metric. Dynamics of Partial Differential Equations 2006,3(4):295–329.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Georgiev, S.G. Blow up of the Solutions of Nonlinear Wave Equation. Bound Value Probl 2007, 042954 (2007). https://doi.org/10.1155/2007/42954
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/42954
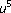 -Klein-Gordon equation. II. Anomalous singularities for semilinear wave equations. In Nonlinear Partial Differential Equations and Their Applications. Collège de France Seminar, Vol. I, Research Notes in Math. Volume 53. Edited by: Breizis H, Lions JL. Pitman, Boston, Mass, USA; 1981:335–364.
-Klein-Gordon equation. II. Anomalous singularities for semilinear wave equations. In Nonlinear Partial Differential Equations and Their Applications. Collège de France Seminar, Vol. I, Research Notes in Math. Volume 53. Edited by: Breizis H, Lions JL. Pitman, Boston, Mass, USA; 1981:335–364.