- Research Article
- Open access
- Published:
Unbounded Supersolutions of Nonlinear Equations with Nonstandard Growth
Boundary Value Problems volume 2007, Article number: 048348 (2006)
Abstract
We show that every weak supersolution of a variable exponent -Laplace equation is lower semicontinuous and that the singular set of such a function is of zero capacity if the exponent is logarithmically Hölder continuous. As a technical tool we derive Harnack-type estimates for possibly unbounded supersolutions.
-Laplace equation is lower semicontinuous and that the singular set of such a function is of zero capacity if the exponent is logarithmically Hölder continuous. As a technical tool we derive Harnack-type estimates for possibly unbounded supersolutions.
References
Zhikov VV: On some variational problems. Russian Journal of Mathematical Physics 1997,5(1):105–116 (1998).
Acerbi E, Fusco N: A transmission problem in the calculus of variations. Calculus of Variations and Partial Differential Equations 1994,2(1):1–16. 10.1007/BF01234312
Acerbi E, Fusco N: Partial regularity under anisotropic
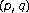 growth conditions. Journal of Differential Equations 1994,107(1):46–67. 10.1006/jdeq.1994.1002
growth conditions. Journal of Differential Equations 1994,107(1):46–67. 10.1006/jdeq.1994.1002Acerbi E, Mingione G: Regularity results for a class of functionals with non-standard growth. Archive for Rational Mechanics and Analysis 2001,156(2):121–140. 10.1007/s002050100117
Marcellini P: Regularity of minimizers of integrals of the calculus of variations with nonstandard growth conditions. Archive for Rational Mechanics and Analysis 1989,105(3):267–284.
Marcellini P: Regularity and existence of solutions of elliptic equations with
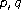 -growth conditions. Journal of Differential Equations 1991,90(1):1–30. 10.1016/0022-0396(91)90158-6
-growth conditions. Journal of Differential Equations 1991,90(1):1–30. 10.1016/0022-0396(91)90158-6Alkhutov YuA: The Harnack inequality and the Hölder property of solutions of nonlinear elliptic equations with a nonstandard growth condition. Differential Equations 1997,33(12):1651–1660, 1726.
Fan X, Zhao D: A class of De Giorgi type and Hölder continuity. Nonlinear Analysis 1999,36(3):295–318. 10.1016/S0362-546X(97)00628-7
Alkhutov YuA, Krasheninnikova OV: Continuity at boundary points of solutions of quasilinear elliptic equations with a nonstandard growth condition. Izvestiya Rossijskoj Akademii Nauk. Seriya Matematicheskaya 2004,68(6):3–60. English translation in Izvestiya: Mathematics 68 (2004), no. 6, 1063–1117
Harjulehto P, Hästö P, Koskenoja M, Varonen S: Sobolev capacity on the space. Journal of Function Spaces and Applications 2003,1(1):17–33.
Heinonen J, Kilpeläinen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York; 1993:vi+363.
Lindqvist P: On the definition and properties of-superharmonic functions. Journal für die reine und angewandte Mathematik 1986, 365: 67–79.
Musielak J: Orlicz Spaces and Modular Spaces, Lecture Notes in Mathematics. Volume 1034. Springer, Berlin; 1983:iii+222.
Kováčik O, Rákosník J: On spacesand. Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.
Fan X, Zhao D: On the spacesand. Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617
Harjulehto P: Variable exponent Sobolev spaces with zero boundary values. preprint, http://www.math.helsinki.fi/analysis/varsobgroup
Hästö P: On the density of smooth functions in variable exponent Sobolev space. to appear in Revista Matemática Iberoamericana
Diening L: Maximal function on generalized Lebesgue spaces. Mathematical Inequalities & Applications 2004,7(2):245–253.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order. Springer, Berlin; 1977:x+401.
Harjulehto P, Hästö P, Koskenoja M, Varonen S: The Dirichlet energy integral and variable exponent Sobolev spaces with zero boundary values. to appear in Potential Analysis, http://www.math.helsinki.fi/analysis/varsobgroup
Harjulehto P, Hästö P, Koskenoja M: The Dirichlet energy integral on intervals in variable exponent Sobolev spaces. Zeitschrift für Analysis und ihre Anwendungen 2003,22(4):911–923.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Harjulehto, P., Kinnunen, J. & Lukkari, T. Unbounded Supersolutions of Nonlinear Equations with Nonstandard Growth. Bound Value Probl 2007, 048348 (2006). https://doi.org/10.1155/2007/48348
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/48348
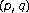 growth conditions. Journal of Differential Equations 1994,107(1):46–67. 10.1006/jdeq.1994.1002
growth conditions. Journal of Differential Equations 1994,107(1):46–67. 10.1006/jdeq.1994.1002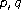 -growth conditions. Journal of Differential Equations 1991,90(1):1–30. 10.1016/0022-0396(91)90158-6
-growth conditions. Journal of Differential Equations 1991,90(1):1–30. 10.1016/0022-0396(91)90158-6