- Research Article
- Open access
- Published:
Existence of Symmetric Positive Solutions for an -Point Boundary Value Problem
-Point Boundary Value Problem
Boundary Value Problems volume 2007, Article number: 079090 (2007)
Abstract
We study the second-order -point boundary value problem
-point boundary value problem ,
, ,
, , where
, where ,
, for
for with
with .
. is continuous, symmetric on the interval
is continuous, symmetric on the interval , and maybe singular at
, and maybe singular at and
and ,
, is continuous, and
is continuous, and is symmetric on the interval
is symmetric on the interval for all
for all and satisfies some appropriate growth conditions. By using Krasnoselskii's fixed point theorem in a cone, we get some existence results of symmetric positive solutions.
and satisfies some appropriate growth conditions. By using Krasnoselskii's fixed point theorem in a cone, we get some existence results of symmetric positive solutions.
References
Chen S, Hu J, Chen L, Wang C:Existence results for
 -point boundary value problem of second order ordinary differential equations. Journal of Computational and Applied Mathematics 2005,180(2):425-432. 10.1016/j.cam.2004.11.010
-point boundary value problem of second order ordinary differential equations. Journal of Computational and Applied Mathematics 2005,180(2):425-432. 10.1016/j.cam.2004.11.010Cheung W-S, Ren J:Positive solution for
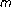 -point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056
-point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056Cheung W-S, Ren J: Twin positive solutions for quasi-linear multi-point boundary value problems. Nonlinear Analysis 2005,62(1):167-177. 10.1016/j.na.2005.03.018
Dong S, Ge W:Positive solutions of an
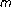 -point boundary value problem with sign changing nonlinearities. Computers & Mathematics with Applications 2005,49(4):589-598. 10.1016/j.camwa.2004.07.018
-point boundary value problem with sign changing nonlinearities. Computers & Mathematics with Applications 2005,49(4):589-598. 10.1016/j.camwa.2004.07.018Guo Y, Shan W, Ge W:Positive solutions for second-order
 -point boundary value problems. Journal of Computational and Applied Mathematics 2003,151(2):415-424. 10.1016/S0377-0427(02)00739-2
-point boundary value problems. Journal of Computational and Applied Mathematics 2003,151(2):415-424. 10.1016/S0377-0427(02)00739-2Infante G, Webb JRL: Nonzero solutions of Hammerstein integral equations with discontinuous kernels. Journal of Mathematical Analysis and Applications 2002,272(1):30-42. 10.1016/S0022-247X(02)00125-7
Kong L, Kong Q: Second-order boundary value problems with nonhomogeneous boundary conditions—I. Mathematische Nachrichten 2005,278(1-2):173-193. 10.1002/mana.200410234
Kosmatov N:Semipositone
 -point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(119):1-7.
-point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(119):1-7.Liu B: Solvability of multi-point boundary value problem at resonance.—part IV. Applied Mathematics and Computation 2003,143(2-3):275-299. 10.1016/S0096-3003(02)00361-2
Liu B: Positive solutions of a nonlinear four-point boundary value problems. Applied Mathematics and Computation 2004,155(1):179-203. 10.1016/S0096-3003(03)00770-7
Liu X:Nontrivial solutions of singular nonlinear
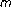 -point boundary value problems. Journal of Mathematical Analysis and Applications 2003,284(2):576-590. 10.1016/S0022-247X(03)00365-2
-point boundary value problems. Journal of Mathematical Analysis and Applications 2003,284(2):576-590. 10.1016/S0022-247X(03)00365-2Ma R:Existence results of a
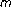 -point boundary value problem at resonance. Journal of Mathematical Analysis and Applications 2004,294(1):147-157. 10.1016/j.jmaa.2004.02.005
-point boundary value problem at resonance. Journal of Mathematical Analysis and Applications 2004,294(1):147-157. 10.1016/j.jmaa.2004.02.005Ma R:Multiple positive solutions for nonlinear
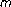 -point boundary value problems. Applied Mathematics and Computation 2004,148(1):249-262. 10.1016/S0096-3003(02)00843-3
-point boundary value problems. Applied Mathematics and Computation 2004,148(1):249-262. 10.1016/S0096-3003(02)00843-3Ma R, O'Regan D:Solvability of singular second order
 -point boundary value problems. Journal of Mathematical Analysis and Applications 2005,301(1):124-134. 10.1016/j.jmaa.2004.07.009
-point boundary value problems. Journal of Mathematical Analysis and Applications 2005,301(1):124-134. 10.1016/j.jmaa.2004.07.009Sun Y:Positive solutions of nonlinear second-order
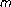 -point boundary value problem. Nonlinear Analysis 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105
-point boundary value problem. Nonlinear Analysis 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105Sun Y: Nontrivial solution for a three-point boundary-value problem. Electronic Journal of Differential Equations 2004,2004(111):1-10.
Sun Y, Liu L: Solvability for a nonlinear second-order three-point boundary value problem. Journal of Mathematical Analysis and Applications 2004,296(1):265-275. 10.1016/j.jmaa.2004.04.013
Xu X:Multiple sign-changing solutions for some
 -point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(89):1-14.
-point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(89):1-14.Xu X:Positive solutions for singular
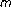 -point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004,291(1):352-367. 10.1016/j.jmaa.2003.11.009
-point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004,291(1):352-367. 10.1016/j.jmaa.2003.11.009Zhang G, Sun J:Positive solutions of
 -point boundary value problems. Journal of Mathematical Analysis and Applications 2004,291(2):406-418. 10.1016/j.jmaa.2003.11.034
-point boundary value problems. Journal of Mathematical Analysis and Applications 2004,291(2):406-418. 10.1016/j.jmaa.2003.11.034Zhang Z, Wang J: On existence and multiplicity of positive solutions to singular multi-point boundary value problems. Journal of Mathematical Analysis and Applications 2004,295(2):502-512. 10.1016/j.jmaa.2004.03.057
Avery RI, Henderson J: Three symmetric positive solutions for a second-order boundary value problem. Applied Mathematics Letters 2000,13(3):1-7. 10.1016/S0893-9659(99)00177-9
Henderson J, Thompson HB: Multiple symmetric positive solutions for a second order boundary value problem. Proceedings of the American Mathematical Society 2000,128(8):2373-2379. 10.1090/S0002-9939-00-05644-6
Li F, Zhang Y: Multiple symmetric nonnegative solutions of second-order ordinary differential equations. Applied Mathematics Letters 2004,17(3):261-267. 10.1016/S0893-9659(04)90061-4
Yao Q:Existence and iteration of
 symmetric positive solutions for a singular two-point boundary value problem. Computers & Mathematics with Applications 2004,47(8-9):1195-1200. 10.1016/S0898-1221(04)90113-7
symmetric positive solutions for a singular two-point boundary value problem. Computers & Mathematics with Applications 2004,47(8-9):1195-1200. 10.1016/S0898-1221(04)90113-7Kosmatov N: Symmetric solutions of a multi-point boundary value problem. Journal of Mathematical Analysis and Applications 2005,309(1):25-36. 10.1016/j.jmaa.2004.11.008
Kosmatov N: A symmetric solution of a multipoint boundary value problem at resonance. Abstract and Applied Analysis 2006, 2006: 11 pages.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Krasnosel'skiĭ MA: Positive Solutions of Operator Equations. P. Noordhoff, Groningen, The Netherlands; 1964:381.
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones. Academic Press, Orlando; 1988.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, Y., Zhang, X. Existence of Symmetric Positive Solutions for an -Point Boundary Value Problem.
Bound Value Probl 2007, 079090 (2007). https://doi.org/10.1155/2007/79090
-Point Boundary Value Problem.
Bound Value Probl 2007, 079090 (2007). https://doi.org/10.1155/2007/79090
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/79090
 -point boundary value problem of second order ordinary differential equations. Journal of Computational and Applied Mathematics 2005,180(2):425-432. 10.1016/j.cam.2004.11.010
-point boundary value problem of second order ordinary differential equations. Journal of Computational and Applied Mathematics 2005,180(2):425-432. 10.1016/j.cam.2004.11.010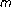 -point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056
-point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056 -point boundary value problem with sign changing nonlinearities. Computers & Mathematics with Applications 2005,49(4):589-598. 10.1016/j.camwa.2004.07.018
-point boundary value problem with sign changing nonlinearities. Computers & Mathematics with Applications 2005,49(4):589-598. 10.1016/j.camwa.2004.07.018 -point boundary value problems. Journal of Computational and Applied Mathematics 2003,151(2):415-424. 10.1016/S0377-0427(02)00739-2
-point boundary value problems. Journal of Computational and Applied Mathematics 2003,151(2):415-424. 10.1016/S0377-0427(02)00739-2 -point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(119):1-7.
-point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(119):1-7. -point boundary value problems. Journal of Mathematical Analysis and Applications 2003,284(2):576-590. 10.1016/S0022-247X(03)00365-2
-point boundary value problems. Journal of Mathematical Analysis and Applications 2003,284(2):576-590. 10.1016/S0022-247X(03)00365-2 -point boundary value problem at resonance. Journal of Mathematical Analysis and Applications 2004,294(1):147-157. 10.1016/j.jmaa.2004.02.005
-point boundary value problem at resonance. Journal of Mathematical Analysis and Applications 2004,294(1):147-157. 10.1016/j.jmaa.2004.02.005 -point boundary value problems. Applied Mathematics and Computation 2004,148(1):249-262. 10.1016/S0096-3003(02)00843-3
-point boundary value problems. Applied Mathematics and Computation 2004,148(1):249-262. 10.1016/S0096-3003(02)00843-3 -point boundary value problems. Journal of Mathematical Analysis and Applications 2005,301(1):124-134. 10.1016/j.jmaa.2004.07.009
-point boundary value problems. Journal of Mathematical Analysis and Applications 2005,301(1):124-134. 10.1016/j.jmaa.2004.07.009 -point boundary value problem. Nonlinear Analysis 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105
-point boundary value problem. Nonlinear Analysis 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105 -point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(89):1-14.
-point boundary-value problems. Electronic Journal of Differential Equations 2004,2004(89):1-14. -point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004,291(1):352-367. 10.1016/j.jmaa.2003.11.009
-point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004,291(1):352-367. 10.1016/j.jmaa.2003.11.009 -point boundary value problems. Journal of Mathematical Analysis and Applications 2004,291(2):406-418. 10.1016/j.jmaa.2003.11.034
-point boundary value problems. Journal of Mathematical Analysis and Applications 2004,291(2):406-418. 10.1016/j.jmaa.2003.11.034 symmetric positive solutions for a singular two-point boundary value problem. Computers & Mathematics with Applications 2004,47(8-9):1195-1200. 10.1016/S0898-1221(04)90113-7
symmetric positive solutions for a singular two-point boundary value problem. Computers & Mathematics with Applications 2004,47(8-9):1195-1200. 10.1016/S0898-1221(04)90113-7