- Research Article
- Open access
- Published:
Robust Monotone Iterates for Nonlinear Singularly Perturbed Boundary Value Problems
Boundary Value Problems volume 2009, Article number: 320606 (2009)
Abstract
This paper is concerned with solving nonlinear singularly perturbed boundary value problems. Robust monotone iterates for solving nonlinear difference scheme are constructed. Uniform convergence of the monotone methods is investigated, and convergence rates are estimated. Numerical experiments complement the theoretical results.
1. Introduction
We are interested in numerical solving of two nonlinear singularly perturbed problems of elliptic and parabolic types.
The first one is the elliptic problem

where  is a positive parameter, and
is a positive parameter, and  is sufficiently smooth function. For
is sufficiently smooth function. For  this problem is singularly perturbed, and the solution has boundary layers near
this problem is singularly perturbed, and the solution has boundary layers near  and
and  (see [1] for details).
(see [1] for details).
The second problem is the one-dimensional parabolic problem

where  is a positive parameter. Under suitable continuity and compatibility conditions on the data, a unique solution of this problem exists. For
is a positive parameter. Under suitable continuity and compatibility conditions on the data, a unique solution of this problem exists. For  problem (1.2) is singularly perturbed and has boundary layers near the lateral boundary of
problem (1.2) is singularly perturbed and has boundary layers near the lateral boundary of  (see [2] for details).
(see [2] for details).
In the study of numerical methods for nonlinear singularly perturbed problems, the two major points to be developed are: (i) constructing robust difference schemes (this means that unlike classical schemes, the error does not increase to infinity, but rather remains bounded, as the small parameter approaches zero); (ii) obtaining reliable and efficient computing algorithms for solving nonlinear discrete problems.
Our goal is to construct a  -uniform numerical method for solving problem (1.1), that is, a numerical method which generates
-uniform numerical method for solving problem (1.1), that is, a numerical method which generates  -uniformly convergent numerical approximations to the solution. We use a numerical method based on the classical difference scheme and the piecewise uniform mesh of Shishkin-type [3]. For solving problem (1.2), we use the implicit difference scheme based on the piecewise uniform mesh in the
-uniformly convergent numerical approximations to the solution. We use a numerical method based on the classical difference scheme and the piecewise uniform mesh of Shishkin-type [3]. For solving problem (1.2), we use the implicit difference scheme based on the piecewise uniform mesh in the  -direction, which converges
-direction, which converges  -uniformly [4].
-uniformly [4].
A major point about the nonlinear difference schemes is to obtain reliable and efficient computational methods for computing the solution. The reliability of iterative techniques for solving nonlinear difference schemes can be essentially improved by using component-wise monotone globally convergent iterations. Such methods can be controlled every time. A fruitful method for the treatment of these nonlinear schemes is the method of upper and lower solutions and its associated monotone iterations [5]. Since an initial iteration in the monotone iterative method is either an upper or lower solution, which can be constructed directly from the difference equation without any knowledge of the exact solution, this method simplifies the search for the initial iteration as is often required in the Newton method. In the context of solving systems of nonlinear equations, the monotone iterative method belongs to the class of methods based on convergence under partial ordering (see [5, Chapter 13] for details).
The purpose of this paper is to construct  -uniformly convergent monotone iterative methods for solving
-uniformly convergent monotone iterative methods for solving  -uniformly convergent nonlinear difference schemes.
-uniformly convergent nonlinear difference schemes.
The structure of the paper is as follows. In Section 2, we prove that the classical difference scheme on the piecewise uniform mesh converges  -uniformly to the solution of problem (1.1). A robust monotone iterative method for solving the nonlinear difference scheme is constructed. In Section 3, we construct a robust monotone iterative method for solving problem (1.2). In the final Section 4, we present numerical experiments which complement the theoretical results.
-uniformly to the solution of problem (1.1). A robust monotone iterative method for solving the nonlinear difference scheme is constructed. In Section 3, we construct a robust monotone iterative method for solving problem (1.2). In the final Section 4, we present numerical experiments which complement the theoretical results.
2. The Elliptic Problem
The following lemma from [1] contains necessary estimates of the solution to (1.1).
Lemma 2.1.
If  is the solution to (1.1), the following estimates hold:
is the solution to (1.1), the following estimates hold:

where constant  is independent of
is independent of  .
.
For  , the boundary layers appear near
, the boundary layers appear near  and
and  .
.
2.1. The Nonlinear Difference Scheme
Introduce a nonuniform mesh 

For solving (1.1), we use the classical difference scheme

where  and
and  . We introduce the linear version of this problem
. We introduce the linear version of this problem

where  . We now formulate a discrete maximum principle for the difference operator
. We now formulate a discrete maximum principle for the difference operator  and give an estimate of the solution to (2.4).
and give an estimate of the solution to (2.4).
Lemma 2.2.
-
(i)
If a mesh function
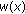 satisfies the conditions
satisfies the conditions 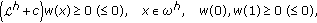 (2.5)
(2.5)
then  ,
,  .
.
-
(ii)
If
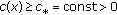 , then the following estimate of the solution to (2.4) holds true:
, then the following estimate of the solution to (2.4) holds true:

where  ,
,  .
.
The proof of the lemma can be found in [6].
2.2. Uniform Convergence on the Piecewise Uniform Mesh
We employ a layer-adapted mesh of a piecewise uniform type [3]. The piecewise uniform mesh is formed in the following manner. We divide the interval  into three parts
into three parts  ,
,  and
and  . Assuming that
. Assuming that  is divisible by
is divisible by  , in the parts
, in the parts  ,
,  we use the uniform mesh with
we use the uniform mesh with  mesh points, and in the part
mesh points, and in the part  the uniform mesh with
the uniform mesh with  mesh points is in use. The transition points
mesh points is in use. The transition points  and
and  are determined by
are determined by

This defines the piecewise uniform mesh. If the parameter  is small enough, then the uniform mesh inside of the boundary layers with the step size
is small enough, then the uniform mesh inside of the boundary layers with the step size  is fine, and the uniform mesh outside of the boundary layers with the step size
is fine, and the uniform mesh outside of the boundary layers with the step size  is coarse, such that
is coarse, such that

In the following theorem, we give the convergence property of the difference scheme (2.3).
Theorem 2.3.
The difference scheme (2.3) on the piecewise uniform mesh (2.8) converges  -uniformly to the solution of (1.1):
-uniformly to the solution of (1.1):

where constant  is independent of
is independent of  and
and  .
.
Proof.
Using Green's function  of the differential operator
of the differential operator  on
on  , we represent the exact solution
, we represent the exact solution  in the form
in the form

where the local Green function  is given by
is given by

and  are defined by
are defined by

Equating the derivatives  and
and  , we get the following integral-difference formula:
, we get the following integral-difference formula:

where here and below we suppress variable  in
in  . Representing
. Representing  on
on  and
and  in the forms
in the forms

the above integral-difference formula can be written as

where the truncation error  of the exact solution
of the exact solution  to (1.1) is defined by
to (1.1) is defined by

From here, it follows that

From Lemma 2.1, the following estimate on  holds:
holds:

We estimate the truncation error  in (2.17) on the interval
in (2.17) on the interval  . Consider the following three cases:
. Consider the following three cases:  ,
,  and
and  . If
. If  , then
, then  , and taking into account that
, and taking into account that  in (2.18), we have
in (2.18), we have

where here and throughout  denotes a generic constant that is independent of
denotes a generic constant that is independent of  and
and  . If
. If  , then
, then  ,
,  . Taking into account that
. Taking into account that  ,
,  and
and  , we have
, we have

If  , then
, then  , and we have
, and we have

Thus,

In a similar way we can estimate  on
on  and conclude that
and conclude that

From here and (2.8), we conclude that

From (2.3), (2.15), by the mean-value theorem, we conclude that  satisfies the difference problem
satisfies the difference problem

Using the assumption on  from (1.1) and (2.24), by (2.6), we prove the theorem.
from (1.1) and (2.24), by (2.6), we prove the theorem.
2.3. The Monotone Iterative Method
In this section, we construct an iterative method for solving the nonlinear difference scheme (2.3) which possesses monotone convergence.
Additionally, we assume that  from (1.1) satisfies the two-sided constraint
from (1.1) satisfies the two-sided constraint

The iterative method is constructed in the following way. Choose an initial mesh function  , then the iterative sequence
, then the iterative sequence  ,
,  , is defined by the recurrence formulae
, is defined by the recurrence formulae

where  is the residual of the difference scheme (2.3) on
is the residual of the difference scheme (2.3) on  .
.
We say that  is an upper solution of (2.3) if it satisfies the inequalities
is an upper solution of (2.3) if it satisfies the inequalities

Similarly,  is called a lower solution if it satisfies the reversed inequalities. Upper and lower solutions satisfy the inequality
is called a lower solution if it satisfies the reversed inequalities. Upper and lower solutions satisfy the inequality

Indeed, by the definition of lower and upper solutions and the mean-value theorem, for  we have
we have

where  . In view of the maximum principle in Lemma 2.2, we conclude the required inequality.
. In view of the maximum principle in Lemma 2.2, we conclude the required inequality.
The following theorem gives the monotone property of the iterative method (2.27).
Theorem 2.4.
Let  ,
,  be upper and lower solutions of (2.3) and
be upper and lower solutions of (2.3) and  satisfy (2.26). Then the upper sequence
satisfy (2.26). Then the upper sequence  generated by (2.27) converges monotonically from above to the unique solution
generated by (2.27) converges monotonically from above to the unique solution  of (2.3), the lower sequence
of (2.3), the lower sequence  generated by (2.27) converges monotonically from below to
generated by (2.27) converges monotonically from below to  :
:

and the sequences converge at the linear rate  .
.
Proof.
We consider only the case of the upper sequence. If  is an upper solution, then from (2.27) we conclude that
is an upper solution, then from (2.27) we conclude that

From Lemma 2.2, by the maximum principle for the difference operator  , it follows that
, it follows that  ,
,  . Using the mean-value theorem and the equation for
. Using the mean-value theorem and the equation for  , we represent
, we represent  in the form
in the form

where  ,
,  . Since the mesh function
. Since the mesh function  is nonpositive on
is nonpositive on  and taking into account (2.26), we conclude that
and taking into account (2.26), we conclude that  is an upper solution. By induction on
is an upper solution. By induction on  , we obtain that
, we obtain that  ,
,  ,
,  , and prove that
, and prove that  is a monotonically decreasing sequence of upper solutions.
is a monotonically decreasing sequence of upper solutions.
We now prove that the monotone sequence  converges to the solution of (2.3). Similar to (2.33), we obtain
converges to the solution of (2.3). Similar to (2.33), we obtain

and from (2.27), it follows that  satisfies the difference equation
satisfies the difference equation

Using (2.26) and (2.6), we have

This proves the convergence of the upper sequence at the linear rate  . Now by linearity of the operator
. Now by linearity of the operator  and the continuity of
and the continuity of  , we have also from (2.27) that the mesh function
, we have also from (2.27) that the mesh function  defined by
defined by

is the exact solution to (2.3). The uniqueness of the solution to (2.3) follows from estimate (2.6). Indeed, if by contradiction, we assume that there exist two solutions  and
and  to (2.3), then by the mean-value theorem, the difference
to (2.3), then by the mean-value theorem, the difference  satisfies the difference problem
satisfies the difference problem

By (2.6),  which leads to the uniqueness of the solution to (2.3). This proves the theorem.
which leads to the uniqueness of the solution to (2.3). This proves the theorem.
Consider the following approach for constructing initial upper and lower solutions  and
and  . Introduce the difference problems
. Introduce the difference problems

where  from (2.26). Then the functions
from (2.26). Then the functions  ,
,  are upper and lower solutions, respectively. We check only that
are upper and lower solutions, respectively. We check only that  is an upper solution. From the maximum principle in Lemma 2.2, it follows that
is an upper solution. From the maximum principle in Lemma 2.2, it follows that  on
on  . Now using the difference equation for
. Now using the difference equation for  and the mean-value theorem, we have
and the mean-value theorem, we have

Since  and
and  is nonnegative, we conclude that
is nonnegative, we conclude that  is an upper solution.
is an upper solution.
Theorem 2.5.
If the initial upper or lower solution  is chosen in the form of (2.39), then the monotone iterative method (2.27) converges
is chosen in the form of (2.39), then the monotone iterative method (2.27) converges  -uniformly to the solution
-uniformly to the solution  of the nonlinear difference scheme (2.3)
of the nonlinear difference scheme (2.3)

Proof.
From (2.27), (2.39), and the mean-value theorem, by (2.6),

From here and estimating  from (2.39) by (2.6),
from (2.39) by (2.6),

we conclude the estimate on  in the form
in the form

where  is defined in the theorem. From here and (2.36), we conclude that
is defined in the theorem. From here and (2.36), we conclude that

Using this estimate, we have

Taking into account that  as
as  , where
, where  is the solution to (2.3), we conclude the theorem.
is the solution to (2.3), we conclude the theorem.
From Theorems 2.3 and 2.5 we conclude the following theorem.
Theorem 2.6.
Suppose that the initial upper or lower solution  is chosen in the form of (2.39). Then the monotone iterative method (2.27) on the piecewise uniform mesh (2.8) converges
is chosen in the form of (2.39). Then the monotone iterative method (2.27) on the piecewise uniform mesh (2.8) converges  -uniformly to the solution of problem (1.1):
-uniformly to the solution of problem (1.1):

where  and constant
and constant  is independent of
is independent of  and
and  .
.
3. The Parabolic Problem
3.1. The Nonlinear Difference Scheme
Introduce uniform mesh  on
on 

For approximation of problem (1.2), we use the implicit difference scheme

where  and
and  are defined in (2.2) and (2.3), respectively. We introduce the linear version of problem (3.2)
are defined in (2.2) and (2.3), respectively. We introduce the linear version of problem (3.2)

We now formulate a discrete maximum principle for the difference operator  and give an estimate of the solution to (3.3).
and give an estimate of the solution to (3.3).
Lemma 3.1.
-
(i)
If a mesh function
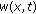 on a time level
on a time level 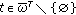 satisfies the conditions
satisfies the conditions 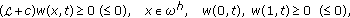 (3.4)
(3.4)
then  ,
,  .
.
-
(ii)
If
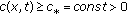 , then the following estimate of the solution to (3.3) holds true:
, then the following estimate of the solution to (3.3) holds true:

where  ,
,  .
.
The proof of the lemma can be found in [6].
3.2. The Monotone Iterative Method
Assume that  from (3.2) satisfies the two-sided constraint
from (3.2) satisfies the two-sided constraint

We consider the following iterative method for solving (3.2). Choose an initial mesh function  . On each time level, the iterative sequence
. On each time level, the iterative sequence  ,
,  , is defined by the recurrence formulae
, is defined by the recurrence formulae

where  is the residual of the difference scheme (3.2) on
is the residual of the difference scheme (3.2) on  .
.
On a time level  , we say that
, we say that  is an upper solution of (3.2) with respect to
is an upper solution of (3.2) with respect to  if it satisfies the inequalities
if it satisfies the inequalities

Similarly,  is called a lower solution if it satisfies all the reversed inequalities. Upper and lower solutions satisfy the inequality
is called a lower solution if it satisfies all the reversed inequalities. Upper and lower solutions satisfy the inequality

This result can be proved in a similar way as for the elliptic problem.
The following theorem gives the monotone property of the iterative method (3.7).
Theorem 3.2.
Assume that  satisfies (3.6). Let
satisfies (3.6). Let  be given and
be given and  ,
,  be upper and lower solutions of (3.2) corresponding
be upper and lower solutions of (3.2) corresponding  . Then the upper sequence
. Then the upper sequence  generated by (3.7) converges monotonically from above to the unique solution
generated by (3.7) converges monotonically from above to the unique solution  of the problem
of the problem

the lower sequence  generated by (3.7) converges monotonically from below to
generated by (3.7) converges monotonically from below to  and the following inequalities hold
and the following inequalities hold

Proof.
We consider only the case of the upper sequence, and the case of the lower sequence can be proved in a similar way.
If  is an upper solution, then from (3.7) we conclude that
is an upper solution, then from (3.7) we conclude that

From Lemma 3.1, it follows that

and from (3.7), it follows that  satisfies the boundary conditions.
satisfies the boundary conditions.
Using the mean-value theorem and the equation for  from (3.7), we represent
from (3.7), we represent  in the form
in the form

where  ,
,  . Since the mesh function
. Since the mesh function  is nonpositive on
is nonpositive on  and taking into account (3.6), we conclude that
and taking into account (3.6), we conclude that  is an upper solution to (3.2). By induction on
is an upper solution to (3.2). By induction on  , we obtain that
, we obtain that  ,
,  ,
,  , and prove that
, and prove that  is a monotonically decreasing sequence of upper solutions.
is a monotonically decreasing sequence of upper solutions.
We now prove that the monotone sequence  converges to the solution of (3.2). The sequence
converges to the solution of (3.2). The sequence  is monotonically decreasing and bounded below by
is monotonically decreasing and bounded below by  , where
, where  is any lower solution (3.9). Now by linearity of the operator
is any lower solution (3.9). Now by linearity of the operator  and the continuity of
and the continuity of  , we have also from (3.7) that the mesh function
, we have also from (3.7) that the mesh function  defined by
defined by

is an exact solution to (3.2). If by contradiction, we assume that there exist two solutions  and
and  to (3.2), then by the mean-value theorem, the difference
to (3.2), then by the mean-value theorem, the difference  satisfies the system
satisfies the system

By Lemma 3.1,  which leads to the uniqueness of the solution to (3.2). This proves the theorem.
which leads to the uniqueness of the solution to (3.2). This proves the theorem.
Consider the following approach for constructing initial upper and lower solutions  and
and  . Introduce the difference problems
. Introduce the difference problems

The functions  ,
,  are upper and lower solutions, respectively. This result can be proved in a similar way as for the elliptic problem.
are upper and lower solutions, respectively. This result can be proved in a similar way as for the elliptic problem.
Theorem 3.3.
Let initial upper or lower solution be chosen in the form of (3.17), and let  satisfy (3.6). Suppose that on each time level the number of iterates
satisfy (3.6). Suppose that on each time level the number of iterates  . Then for the monotone iterative methods (3.7), the following estimate on convergence rate holds:
. Then for the monotone iterative methods (3.7), the following estimate on convergence rate holds:

where  is the solution to (3.2),
is the solution to (3.2),  , and constant
, and constant  is independent of
is independent of  ,
,  and
and  .
.
Proof.
Similar to (3.14), using the mean-value theorem and the equation for  from (3.7), we have
from (3.7), we have

From here and (3.7), we have

Using (3.5) and (3.6), we have

where  is defined in (3.18).
is defined in (3.18).
Introduce the notation

where  . Using the mean-value theorem, from (3.2) and (3.19), we conclude that
. Using the mean-value theorem, from (3.2) and (3.19), we conclude that  satisfies the problem
satisfies the problem

where  , and we have taken into account that
, and we have taken into account that  . By (3.5), (3.6), and (3.21),
. By (3.5), (3.6), and (3.21),

Using (3.6), (3.17), and the mean-value theorem, estimate  from (3.7) by (3.5),
from (3.7) by (3.5),

where  is independent of
is independent of  (
( ),
),  and
and  . Thus,
. Thus,

Similarly, from (3.2) and (3.19), it follows that

Using (3.21), by (3.5),

Using (3.17), estimate  from (3.7) by (3.5),
from (3.7) by (3.5),

where  . As follows from Theorem 3.2, the monotone sequences
. As follows from Theorem 3.2, the monotone sequences  and
and  are bounded from above and below by, respectively,
are bounded from above and below by, respectively,  and
and  . Applying (3.5) to problem (3.17) at
. Applying (3.5) to problem (3.17) at  , we have
, we have

where constant  is independent of
is independent of  ,
,  and
and  . Thus, we prove that
. Thus, we prove that  is independent of
is independent of  ,
,  and
and  . From (3.26) and (3.28), we conclude
. From (3.26) and (3.28), we conclude

By induction on  , we prove
, we prove

where all constants  are independent of
are independent of  ,
,  and
and  . Taking into account that
. Taking into account that  , we prove the estimate (3.18) with
, we prove the estimate (3.18) with  .
.
In [4], we prove that the difference scheme (3.2) on the piecewise uniform mesh (2.8) converges  -uniformly to the solution of problem (1.2):
-uniformly to the solution of problem (1.2):

where  is the exact solution to (3.2), and constant
is the exact solution to (3.2), and constant  is independent of
is independent of  ,
,  and
and  . From here and Theorem 3.3, we conclude the following theorem.
. From here and Theorem 3.3, we conclude the following theorem.
Theorem 3.4.
Suppose that on each time level the initial upper or lower solution  is chosen in the form of (3.17) and
is chosen in the form of (3.17) and  . Then the monotone iterative method (3.7) on the piecewise uniform mesh (2.8) converges
. Then the monotone iterative method (3.7) on the piecewise uniform mesh (2.8) converges  -uniformly to the solution of problem (1.2):
-uniformly to the solution of problem (1.2):

where  , and constant
, and constant  is independent of
is independent of  ,
,  and
and  .
.
4. Numerical Experiments
It is found that in all numerical experiments the basic feature of monotone convergence of the upper and lower sequences is observed. In fact, the monotone property of the sequences holds at every mesh point in the domain. This is, of course, to be expected from the analytical consideration.
4.1. The Elliptic Problem
Consider problem (1.1) with  . We mention that
. We mention that  is the solution of the reduced problem, where
is the solution of the reduced problem, where  . This problem gives
. This problem gives  ,
,  , and initial lower and upper solutions are chosen in the form of (2.39). The stopping criterion for the monotone iterative method (2.27) is
, and initial lower and upper solutions are chosen in the form of (2.39). The stopping criterion for the monotone iterative method (2.27) is

Our numerical experiments show that for  and
and  , iteration counts for monotone method (2.27) on the piecewise uniform mesh are independent of
, iteration counts for monotone method (2.27) on the piecewise uniform mesh are independent of  and
and  , and equals 12 and 8 for the lower and upper sequences, respectively. These numerical results confirm our theoretical results stated in Theorem 2.5.
, and equals 12 and 8 for the lower and upper sequences, respectively. These numerical results confirm our theoretical results stated in Theorem 2.5.
In Table 1, we present numbers of iterations for solving the test problem by the Newton iterative method with the initial iterations  ,
,  . Here
. Here  is in use, and we denote by an "*" if more than 100 iterations is needed to satisfy the stopping criterion, or if the method diverges. The numerical results indicate that the Newton method cannot be used successfully for this test problem.
is in use, and we denote by an "*" if more than 100 iterations is needed to satisfy the stopping criterion, or if the method diverges. The numerical results indicate that the Newton method cannot be used successfully for this test problem.
4.2. The Parabolic Problem
For the parabolic problem (1.2), we consider the test problem with  and
and  . This problem gives
. This problem gives  ,
,  , and the initial lower and upper solutions are chosen in the form of (3.17).
, and the initial lower and upper solutions are chosen in the form of (3.17).
The stopping test for the monotone method (3.7) is defined by

Our numerical experiments show that for  and
and  , on each time level the number of iterations for monotone method (3.7) on the piecewise uniform mesh is independent of
, on each time level the number of iterations for monotone method (3.7) on the piecewise uniform mesh is independent of  and
and  and equal 4, 4, and 3 for
and equal 4, 4, and 3 for  , respectively. These numerical results confirm our theoretical results stated in Theorem 3.3.
, respectively. These numerical results confirm our theoretical results stated in Theorem 3.3.
References
Boglaev I: Approximate solution of a non-linear boundary value problem with a small parameter for the highest-order differential. USSR Computational Mathematics and Mathematical Physics 1984, 24(6):30–35. 10.1016/0041-5553(84)90005-3
Boglaev I: Numerical method for quasi-linear parabolic equation with boundary layer. USSR Computational Mathematics and Mathematical Physics 1990, 30: 716–726.
Miller JJH, O'Riordan E, Shishkin GI: Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions. World Scientific, Singapore; 1996:xiv+166.
Boglaev I, Hardy M: Uniform convergence of a weighted average scheme for a nonlinear reaction-diffusion problem. Journal of Computational and Applied Mathematics 2007, 200(2):705–721. 10.1016/j.cam.2006.01.026
Ortega JM, Rheinboldt WC: Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York, NY, USA; 1970:xx+572.
Samarskii AA: The Theory of Difference Schemes, Monographs and Textbooks in Pure and Applied Mathematics. Volume 240. Marcel Dekker, New York, NY, USA; 2001:xviii+761.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boglaev, I. Robust Monotone Iterates for Nonlinear Singularly Perturbed Boundary Value Problems. Bound Value Probl 2009, 320606 (2009). https://doi.org/10.1155/2009/320606
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/320606
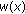 satisfies the conditions
satisfies the conditions 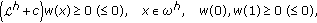
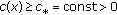 , then the following estimate of the solution to (2.4) holds true:
, then the following estimate of the solution to (2.4) holds true: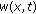 on a time level
on a time level 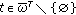 satisfies the conditions
satisfies the conditions 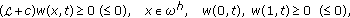
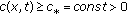 , then the following estimate of the solution to (3.3) holds true:
, then the following estimate of the solution to (3.3) holds true: