- Research Article
- Open access
- Published:
Existence of Periodic Solution for a Nonlinear Fractional Differential Equation
Boundary Value Problems volume 2009, Article number: 324561 (2009)
Abstract
We study the existence of solutions for a class of fractional differential equations. Due to the singularity of the possible solutions, we introduce a new and proper concept of periodic boundary value conditions. We present Green's function and give some existence results for the linear case and then we study the nonlinear problem.
1. Introduction
Fractional calculus is a generalization of ordinary differentiation and integration to arbitrary noninteger order. The subject is as old as the differential calculus, and goes back to time when Leibnitz and Newton invented differential calculus. The idea of fractional calculus has been a subject of interest not only among mathematicians but also among physicists and engineers. See, for instance, [1–6].
Fractional-order models are more accurate than integer-order models, that is, there are more degrees of freedom in the fractional-order models. Furthermore, fractional derivatives provide an excellent instrument for the description of memory and hereditary properties of various materials and processes due to the existence of a "memory" term in a model. This memory term insures the history and its impact to the present and future. For more details, see [7].
Fractional calculus appears in rheology, viscoelasticity, electrochemistry, electromagnetism, and so forth. For details, see the monographs of Kilbas et al. [8], Kiryakova [9], Miller and Ross [10], Podlubny [11], Oldham and Spanier [12], and Samko et al. [13], and the papers of Diethelm et al. [14–16], Mainardi [17], Metzler et al. [18], Podlubny et al. [19], and the references therein. For some recent advances on fractional calculus and differential equations, see [1, 3, 20–24].
In this paper we consider the following nonlinear fractional differential equation of the form

where  is the standard Riemann-Liouville fractional derivative,
is the standard Riemann-Liouville fractional derivative,  is continuous, and
is continuous, and  .
.
This paper is organized as follows. in Section 2 we recall some definitions of fractional integral and derivative and related basic properties which will be used in the sequel. In Section 3, we deal with the linear case where  is a continuous function. Section 4 is devoted to the nonlinear case.
is a continuous function. Section 4 is devoted to the nonlinear case.
2. Preliminary Results
In this section, we introduce notations, definitions, and preliminary facts which are used throughout this paper.
Let  the Banach space of all continuous real functions defined on
the Banach space of all continuous real functions defined on  with the norm
with the norm  Define for
Define for  ,
,  . Let
. Let  ,
,  be the space of all functions
be the space of all functions  such that
such that  which turn out to be a Banach space when endowed with the norm
which turn out to be a Banach space when endowed with the norm 
By  we denote the space of all real functions defined on
we denote the space of all real functions defined on  which are Lebesgue integrable.
which are Lebesgue integrable.
Obviously  if
if 
Definition 2.1 (see [11, 13]).
The Riemann-Liouville fractional primitive of order  of a function
of a function  is given by
is given by

provided the right side is pointwise defined on  , and where
, and where  is the gamma function.
is the gamma function.
For instance,  exists for all
exists for all  , when
, when  ; note also that when
; note also that when  , then
, then  and moreover
and moreover 
Let  , if
, if  with
with  , then
, then  , with
, with  If
If  , then
, then  is bounded at the origin, whereas if
is bounded at the origin, whereas if  with
with  , then we may expect
, then we may expect  to be unbounded at the origin.
to be unbounded at the origin.
Recall that the law of composition  holds for all
holds for all 
Definition 2.2 (see [11, 13]).
The Riemann-Liouville fractional derivative of order  of a continuous function
of a continuous function  is given by
is given by

We have  for all
for all  .
.
Lemma 2.3.
Let  . If one assumes
. If one assumes  , then the fractional differential equation
, then the fractional differential equation

has  , as unique solutions.
, as unique solutions.
From this lemma we deduce the following law of composition.
Proposition 2.4.
Assume that  is in
is in  with a fractional derivative of order
with a fractional derivative of order  that belongs to
that belongs to  . Then
. Then

for some  .
.
If  with
with  and
and  , then
, then  .
.
3. Linear Problem
In this section, we will be concerned with the following linear fractional differential equation:

where  , and
, and  is a continuous function.
is a continuous function.
Before stating our main results for this section, we study the equation

Then

for some  .
.
Note that  and
and  . However,
. However,  since
since  has a singularity at
has a singularity at  for
for 
It is easy to show that  . Hence we should look for solutions, not in
. Hence we should look for solutions, not in  but in
but in  . We cannot consider the usual initial condition
. We cannot consider the usual initial condition  , but
, but  Hence, to study the periodic boundary value problem, one has to consider the following boundary condition of periodic type
Hence, to study the periodic boundary value problem, one has to consider the following boundary condition of periodic type

From (3.3), we have

that leads to the following.
Theorem 3.1.
The periodic boundary value problem (3.2)–(3.4) has a unique solution  if and only if
if and only if

The previous result remains true even if  . In this case, (3.2) is reduced to the ordinary differential equation
. In this case, (3.2) is reduced to the ordinary differential equation

with the periodic boundary condition

and the condition (3.6) is reduced to the classical one:

Now, for  different from
different from  , consider the homogenous linear equation
, consider the homogenous linear equation

The solution is given by

Indeed, we have

since the series representing  is absolutely convergent.
is absolutely convergent.
Using the identities

we get

Then

Note that the solution can be expressed by means of the classical Mittag-Leffler special functions [8]. Indeed

The previous formula remains valid for  . In this case,
. In this case,

Then

which is the classical solution to the homogeneous linear differential equation

Now, consider the nonhomogeneous problem (3.1). We seek the particular solution in the following form:

It suffices to show that

Indeed

Using the change of variable

we get

Then,

Hence, the general solution of the nonhomogeneous equation (3.1) takes the form

Now, consider the periodic boundary value problem (3.1)–(3.4). Its unique solution is given by (3.26) for some  . Also
. Also  is in
is in  and
and

From (3.26), we have

which leads to

since  for any
for any  , we have
, we have

Then the solution of the problem (3.1)–(3.4) is given by

Thus we have the following result.
Theorem 3.2.
The periodic boundary value problem (3.1)–(3.4) has a unique solution  given by
given by

where

For  ,
,  given,
given,  is bounded on
is bounded on  .
.
For  , (3.1) is
, (3.1) is

and the boundary condition (3.4) is

In this situation Green's function is

which is precisely Green's function for the periodic boundary value problem considered in [25, 26].
4. Nonlinear Problem
In this section we will be concerned with the existence and uniqueness of solution to the nonlinear problem (1.1)–(3.4). To this end, we need the following fixed point theorem of Schaeffer.
Theorem 4.1.
Assume  to be a normed linear space, and let operator
to be a normed linear space, and let operator  be compact. Then either
be compact. Then either
(i)the operator  has a fixed point in
has a fixed point in  , or
, or
(ii)the set  is unbounded.
is unbounded.
If  is a solution of problem (1.1)–(3.4), then it is given by
is a solution of problem (1.1)–(3.4), then it is given by

where  is Green's function defined in Theorem 3.2.
is Green's function defined in Theorem 3.2.
Define the operator  by
by

Then the problem (1.1)–(3.4) has solutions if and only if the operator equation  has fixed points.
has fixed points.
Lemma 4.2.
Suppose that the following hold:
(i)there exists a constant  such that
such that

(ii)there exists a constant  such that
such that

Then the operator  is well defined, continuous, and compact.
is well defined, continuous, and compact.
Proof.
-
(a)
We check, using hypothesis (4.3), that
 , for every
, for every 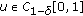 . Indeed, for any
. Indeed, for any 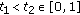 ,
, 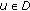 , we have
, we have 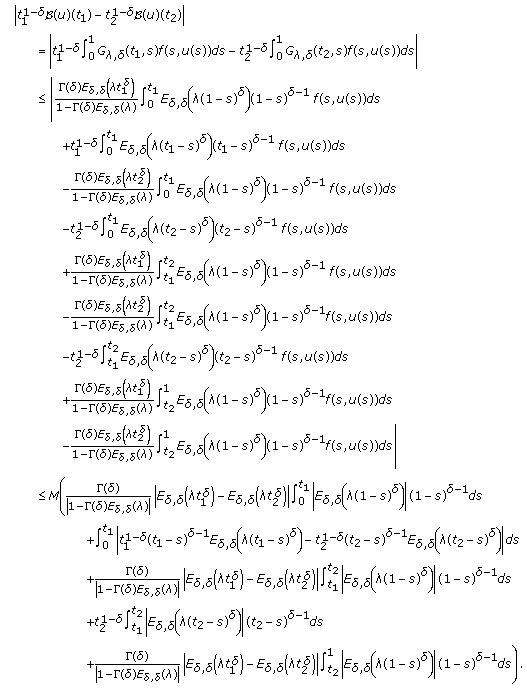 (4.5)
(4.5)
From the previous expression, we deduce that, if  , then
, then

Indeed, note that the integral  is bounded by
is bounded by

A similar argument is useful to study the behavior of the last three terms of the long inequality above. On the other hand, if we denote by  the second term in the right-hand side of that inequality, then it is satisfied that
the second term in the right-hand side of that inequality, then it is satisfied that

Note that

and, concerning  , we distinguish two cases. If
, we distinguish two cases. If  is such that
is such that  , then
, then

and, if  is such that
is such that  , then
, then

In consequence,

The first term in the right-hand side of the previous inequality clearly tends to zero as  . On the other hand, denoting by
. On the other hand, denoting by  the integer part function, we have
the integer part function, we have

The finite sum obviously has limit zero as  . The infinite sum is equal to
. The infinite sum is equal to

and its limit as  is zero. Note that
is zero. Note that  is bounded above by
is bounded above by  .
.
The previous calculus shows that  , for
, for  , hence we can define
, hence we can define  .
.
-
(b)
Next, we prove that
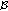 is continuous.
is continuous.
Note that, for  and for every
and for every  , we have, using hypothesis (4.4),
, we have, using hypothesis (4.4),

Using the definition of  , we get
, we get

Moreover,

Using that  for
for  ,
,  for
for  , and
, and  for
for  we obtain
we obtain

Note that the Beta function, also called the Euler integral of the first kind,

where  and
and  , satisfies that
, satisfies that  . In particular,
. In particular,  . On the other hand, using the change of variable
. On the other hand, using the change of variable  , we deduce that
, we deduce that

This proves that

Hence,

In consequence,

Finally, we check that  is compact. Let
is compact. Let  be a bounded set in
be a bounded set in  .
.
-
(i)
First, we check that
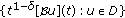 is a bounded set in
is a bounded set in  .
.
Indeed,

Hence

and then

which implies that  is a bounded set in
is a bounded set in  .
.
-
(ii)
Now, we prove that
 is an equicontinuous set in
is an equicontinuous set in  . Following the calculus in (a), we show that
. Following the calculus in (a), we show that 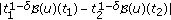 tends to zero as
tends to zero as 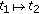 .
.
Then  is equicontinuous in the space
is equicontinuous in the space  , where
, where  , for
, for  .
.
As a consequence of (i) and (ii),  is a bounded and equicontinuous set in the space
is a bounded and equicontinuous set in the space  .
.
Hence, for a sequence  in
in  ,
,  has a subsequence converging to
has a subsequence converging to  , that is,
, that is,

Taking  , we get
, we get

which means that  , which proves that
, which proves that  is compact.
is compact.
Theorem 4.3.
Assume that (4.3) and (4.4) hold. Then the problem (1.1)–(3.4) has at least one solution in 
Proof.
Consider the set  .
.
Let  be any element of
be any element of  , then
, then  for some
for some  . Thus for each
. Thus for each  , we have
, we have

As in Lemma 4.2, (i), we have

which implies that the set  is bounded independently of
is bounded independently of  . Using Lemma 4.2 and Theorem 4.1, we obtain that the operator
. Using Lemma 4.2 and Theorem 4.1, we obtain that the operator  has at least a fixed point.
has at least a fixed point.
Remark 4.4.
In Lemma 4.2, condition (4.3) is used to prove that the operator  is continuous. Hence, in Lemma 4.2 and, in consequence, in Theorem 4.3, we can assume the weaker condition.
is continuous. Hence, in Lemma 4.2 and, in consequence, in Theorem 4.3, we can assume the weaker condition.
(i)For each  fixed, there exists
fixed, there exists  such that
such that

instead of (4.3).
However, to prove the existence and uniqueness of solution given in the following theorem, we need to assume the Lipschitzian character of  (condition (4.3).
(condition (4.3).
Theorem 4.5.
Assume that (4.4) holds. Then the problem (1.1)–(3.4) has a unique solution in  provided that
provided that

Proof.
We use the Banach contraction principle to prove that the operator  has a unique fixed point.
has a unique fixed point.
Using the calculus in (b) Lemma 4.2,  is a contraction by condition (4.32). As a consequence of Banach fixed point theorem, we deduce that
is a contraction by condition (4.32). As a consequence of Banach fixed point theorem, we deduce that  has a unique fixed point which gives rise to a unique solution of problem (1.1)–(3.4).
has a unique fixed point which gives rise to a unique solution of problem (1.1)–(3.4).
Remark 4.6.
If  , condition (4.32) is reduced to
, condition (4.32) is reduced to

References
Ahmad B, Nieto JJ: Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions. preprint
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
Benchohra M, Cabada A, Seba D: An existence result for nonlinear fractional differential equations on Banach spaces. Boundary Value Problems 2009, 2009:-11.
Bonilla B, Rivero M, Rodríguez-Germá L, Trujillo JJ: Fractional differential equations as alternative models to nonlinear differential equations. Applied Mathematics and Computation 2007, 187(1):79–88. 10.1016/j.amc.2006.08.105
Daftardar-Gejji V, Bhalekar S: Boundary value problems for multi-term fractional differential equations. Journal of Mathematical Analysis and Applications 2008, 345(2):754–765. 10.1016/j.jmaa.2008.04.065
Varlamov V: Differential and integral relations involving fractional derivatives of Airy functions and applications. Journal of Mathematical Analysis and Applications 2008, 348(1):101–115. 10.1016/j.jmaa.2008.06.052
Lazarević MP, Spasić AM: Finite-time stability analysis of fractional order time-delay systems: Gronwall's approach. Mathematical and Computer Modelling 2009, 49(3–4):475–481. 10.1016/j.mcm.2008.09.011
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier Science B.V., Amsterdam, The Netherlands; 2006:xvi+523.
Kiryakova V: Generalized Fractional Calculus and Applications, Pitman Research Notes in Mathematics Series. Volume 301. Longman Scientific & Technical, Harlow, UK; 1994:x+388.
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Podlubny I: Fractional Differential Equations, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York, NY, USA; 1974:xiii+234.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives. Theory and Applications. Gordon and Breach Science, Yverdon, Switzerland; 1993:xxxvi+976.
Diethelm K, Freed AD: On the solution of nonlinear fractional order differential equations used in the modeling of viscoplasticity. In Scientifice Computing in Chemical Engineering II-Computational Fluid Dynamics, Reaction Engineering and Molecular Properties. Edited by: Keil F, Mackens W, Voss H, Werther J. Springer, Heidelberg, Germany; 1999:217–224.
Diethelm K, Ford NJ: Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications 2002, 265(2):229–248. 10.1006/jmaa.2000.7194
Diethelm K, Walz G: Numerical solution of fractional order differential equations by extrapolation. Numerical Algorithms 1997, 16(3–4):231–253.
Mainardi F: Fractional calculus: some basic problems in continuum and statistical mechanis. In Fractals and Fractional Calculus in Continuum Mechanics. Edited by: Carpinteri A, Mainardi F. Springer, Wien, Austria; 1997:291–348.
Metzler R, Schick W, Kilian H-G, Nonnenmacher TF: Relaxation in filled polymers: a fractional calculus approach. The Journal of Chemical Physics 1995, 103(16):7180–7186. 10.1063/1.470346
Podlubny I, Petráš I, Vinagre BM, O'Leary P, Dorčák L: Analogue realizations of fractional-order controllers. Nonlinear Dynamics 2002, 29(1–4):281–296.
Araya D, Lizama C: Almost automorphic mild solutions to fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(11):3692–3705. 10.1016/j.na.2007.10.004
Benchohra M, Hamani S, Nieto JJ, Slimani BA: Existence results for fractional differential inclusions with fractional order and impulses. to appear in Computers & Mathematics with Applications
Chang Y-K, Nieto JJ: Some new existence results for fractional differential inclusions with boundary conditions. Mathematical and Computer Modelling 2009, 49(3–4):605–609. 10.1016/j.mcm.2008.03.014
Chang Y-K, Nieto JJ: Existence of solutions for impulsive neutral integro-differential inclusions with nonlocal initial conditions via fractional operators. Numerical Functional Analysis and Optimization 2009, 30: 227–244. 10.1080/01630560902841146
Jafari H, Seifi S: Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation. Communications in Nonlinear Science and Numerical Simulation 2009, 14(5):2006–2012. 10.1016/j.cnsns.2008.05.008
Li J, Nieto JJ, Shen J: Impulsive periodic boundary value problems of first-order differential equations. Journal of Mathematical Analysis and Applications 2007, 325(1):226–236. 10.1016/j.jmaa.2005.04.005
Nieto JJ: Differential inequalities for functional perturbations of first-order ordinary differential equations. Applied Mathematics Letters 2002, 15(2):173–179. 10.1016/S0893-9659(01)00114-8
Acknowledgment
The research of J. J. Nieto and R. Rodríguez-López has been partially supported by Ministerio de Educacion y Ciencia and FEDER, project MTM2007-61724, and by Xunta de Galicia and FEDER, project PGIDIT06PXIB207023PR.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Belmekki, M., Nieto, J. & Rodríguez-López, R. Existence of Periodic Solution for a Nonlinear Fractional Differential Equation. Bound Value Probl 2009, 324561 (2009). https://doi.org/10.1155/2009/324561
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/324561
 , for every
, for every 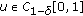 . Indeed, for any
. Indeed, for any 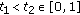 ,
, 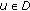 , we have
, we have 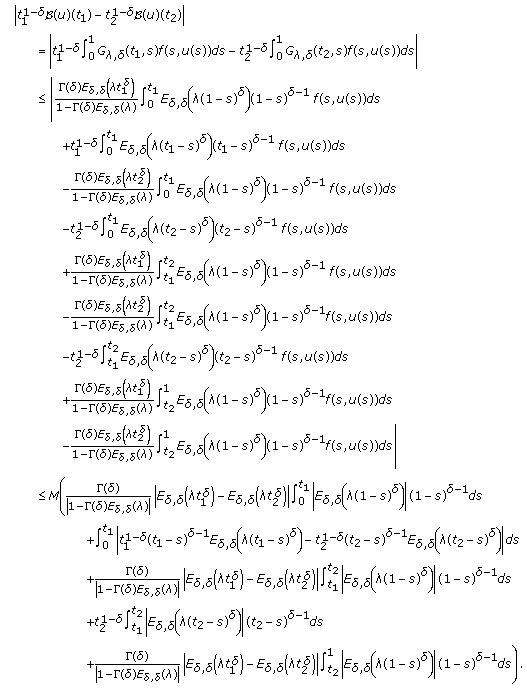
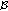 is continuous.
is continuous.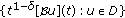 is a bounded set in
is a bounded set in  .
. is an equicontinuous set in
is an equicontinuous set in  . Following the calculus in (a), we show that
. Following the calculus in (a), we show that 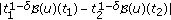 tends to zero as
tends to zero as 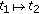 .
.