- Research Article
- Open access
- Published:
New Results on Multiple Solutions for  th-Order Fuzzy Differential Equations under Generalized Differentiability
th-Order Fuzzy Differential Equations under Generalized Differentiability
Boundary Value Problems volume 2009, Article number: 395714 (2009)
Abstract
We firstly present a generalized concept of higher-order differentiability for fuzzy functions. Then we interpret  th-order fuzzy differential equations using this concept. We introduce new definitions of solution to fuzzy differential equations. Some examples are provided for which both the new solutions and the former ones to the fuzzy initial value problems are presented and compared. We present an example of a linear second-order fuzzy differential equation with initial conditions having four different solutions.
th-order fuzzy differential equations using this concept. We introduce new definitions of solution to fuzzy differential equations. Some examples are provided for which both the new solutions and the former ones to the fuzzy initial value problems are presented and compared. We present an example of a linear second-order fuzzy differential equation with initial conditions having four different solutions.
1. Introduction
The term "fuzzy differential equation" was coined in 1987 by Kandel and Byatt [1] and an extended version of this short note was published two years later [2]. There are many suggestions to define a fuzzy derivative and in consequence, to study fuzzy differential equation [3]. One of the earliest was to generalize the Hukuhara derivative of a set-valued function. This generalization was made by Puri and Ralescu [4] and studied by Kaleva [5]. It soon appeared that the solution of fuzzy differential equation interpreted by Hukuhara derivative has a drawback: it became fuzzier as time goes by [6]. Hence, the fuzzy solution behaves quite differently from the crisp solution. To alleviate the situation, Hüllermeier [7] interpreted fuzzy differential equation as a family of differential inclusions. The main shortcoming of using differential inclusions is that we do not have a derivative of a fuzzy-number-valued function.
The strongly generalized differentiability was introduced in [8] and studied in [9–11]. This concept allows us to solve the above-mentioned shortcoming. Indeed, the strongly generalized derivative is defined for a larger class of fuzzy-number-valued functions than the Hukuhara derivative. Hence, we use this differentiability concept in the present paper. Under this setting, we obtain some new results on existence of several solutions for  th-order fuzzy differential equations. Higher-order fuzzy differential equation with Hukuhara differentiability is considered in [12] and the existence and uniqueness of solution for nonlinearities satisfying a Lipschitz condition is proved. Buckley and Feuring [13] presented two different approaches to the solvability of
th-order fuzzy differential equations. Higher-order fuzzy differential equation with Hukuhara differentiability is considered in [12] and the existence and uniqueness of solution for nonlinearities satisfying a Lipschitz condition is proved. Buckley and Feuring [13] presented two different approaches to the solvability of  th-order linear fuzzy differential equations.
th-order linear fuzzy differential equations.
Here, using the concept of generalized derivative and its extension to higher-order derivatives, we show that we have several possibilities or types to define higher-order derivatives of fuzzy-number-valued functions. Then, we propose a new method to solve higher-order fuzzy differential equations based on the selection of derivative type covering all former solutions. With these ideas, the selection of derivative type in each step of derivation plays a crucial role.
2. Preliminaries
In this section, we give some definitions and introduce the necessary notation which will be used throughout this paper. See, for example, [6].
Definition 2.1.
Let  be a nonempty set. A fuzzy set
be a nonempty set. A fuzzy set  in
in  is characterized by its membership function
is characterized by its membership function  Thus,
Thus,  is interpreted as the degree of membership of an element
is interpreted as the degree of membership of an element  in the fuzzy set
in the fuzzy set  for each
for each 
Let us denote by  the class of fuzzy subsets of the real axis (i.e.,
the class of fuzzy subsets of the real axis (i.e.,  ) satisfying the following properties:
) satisfying the following properties:
(i) is normal, that is, there exists
is normal, that is, there exists  such that
such that 
(ii) is convex fuzzy set (i.e.,
is convex fuzzy set (i.e.,  ),
),
(iii) is upper semicontinuous on
is upper semicontinuous on  ,
,
(iv) is compact where
is compact where  denotes the closure of a subset.
denotes the closure of a subset.
Then  is called the space of fuzzy numbers. Obviously,
is called the space of fuzzy numbers. Obviously,  . For
. For  denote
denote  and
and  . If
. If  belongs to
belongs to  then
then  -level set
-level set  is a nonempty compact interval for all
is a nonempty compact interval for all  . The notation
. The notation

denotes explicitly the  -level set of
-level set of  . One refers to
. One refers to  and
and  as the lower and upper branches of
as the lower and upper branches of  , respectively. The following remark shows when
, respectively. The following remark shows when  is a valid
is a valid  -level set.
-level set.
Remark 2.2 (see [6]).
The sufficient conditions for  to define the parametric form of a fuzzy number are as follows:
to define the parametric form of a fuzzy number are as follows:
(i) is a bounded monotonic increasing (nondecreasing) left-continuous function on
is a bounded monotonic increasing (nondecreasing) left-continuous function on  and right-continuous for
and right-continuous for  ,
,
(ii) is a bounded monotonic decreasing (nonincreasing) left-continuous function on
is a bounded monotonic decreasing (nonincreasing) left-continuous function on  and right-continuous for
and right-continuous for  ,
,
(iii)
For  and
and  , the sum
, the sum  and the product
and the product  are defined by
are defined by  where
where  means the usual addition of two intervals (subsets) of
means the usual addition of two intervals (subsets) of  and
and  means the usual product between a scalar and a subset of
means the usual product between a scalar and a subset of 
The metric structure is given by the Hausdorff distance:

by

The following properties are wellknown:
(i)
(ii)
(iii)
and  is a complete metric space.
is a complete metric space.
Definition 2.3.
Let  . If there exists
. If there exists  such that
such that  then
then  is called the
is called the  -difference of
-difference of  and it is denoted
and it is denoted  .
.
In this paper the sign " " stands always for
" stands always for  -difference and let us remark that
-difference and let us remark that  in general. Usually we denote
in general. Usually we denote  by
by  , while
, while  stands for the
stands for the  -difference.
-difference.
3. Generalized Fuzzy Derivatives
The concept of the fuzzy derivative was first introduced by Chang and Zadeh [14]; it was followed up by Dubois and Prade [15] who used the extension principle in their approach. Other methods have been discussed by Puri and Ralescu [4], Goetschel and Voxman [16], Kandel and Byatt [1, 2]. Lakshmikantham and Nieto introduced the concept of fuzzy differential equation in a metric space [17]. Puri and Ralescu in [4] introduced H-derivative (differentiability in the sense of Hukuhara) for fuzzy mappings and it is based on the  -difference of sets, as follows. Henceforth, we suppose
-difference of sets, as follows. Henceforth, we suppose  for
for 
Definition 3.1.
Let  be a fuzzy function. One says,
be a fuzzy function. One says,  is differentiable at
is differentiable at  if there exists an element
if there exists an element  such that the limits
such that the limits

exist and are equal to  Here the limits are taken in the metric space
Here the limits are taken in the metric space 
The above definition is a straightforward generalization of the Hukuhara differentiability of a set-valued function. From [6, Proposition 4.2.8], it follows that Hukuhara differentiable function has increasing length of support. Note that this definition of derivative is very restrictive; for instance, in [9], the authors showed that if  where
where  is a fuzzy number and
is a fuzzy number and  is a function with
is a function with  , then
, then  is not differentiable. To avoid this difficulty, the authors [9] introduced a more general definition of derivative for fuzzy-number-valued function. In this paper, we consider the following definition [11].
is not differentiable. To avoid this difficulty, the authors [9] introduced a more general definition of derivative for fuzzy-number-valued function. In this paper, we consider the following definition [11].
Definition 3.2.
Let  and fix
and fix  One says
One says  is (1)-differentiable at
is (1)-differentiable at  , if there exists an element
, if there exists an element  such that for all
such that for all  sufficiently near to
sufficiently near to  , there exist
, there exist  and the limits (in the metric
and the limits (in the metric  )
)

 is (2)-differentiable if for all
is (2)-differentiable if for all  sufficiently near to
sufficiently near to  , there exist
, there exist  and the limits (in the metric
and the limits (in the metric  )
)

If  is
is  -differentiable at
-differentiable at  , we denote its first derivatives by
, we denote its first derivatives by  , for
, for 
Example 3.3.
Let  and define
and define  by
by  for all
for all  . If
. If  is differentiable at
is differentiable at  , then
, then  is generalized differentiable on
is generalized differentiable on  and we have
and we have  . For instance, if
. For instance, if  ,
,  is (1)-differentiable. If
is (1)-differentiable. If  then
then  is (2)-differentiable.
is (2)-differentiable.
Remark 3.4.
In the previous definition, (1)-differentiability corresponds to the H-derivative introduced in [4], so this differentiability concept is a generalization of the H-derivative and obviously more general. For instance, in the previous example, for  with
with  we have
we have  .
.
Remark 3.5.
In [9], the authors consider four cases for derivatives. Here we only consider the two first cases of [9, Definition 5]. In the other cases, the derivative is trivial because it is reduced to crisp element (more precisely,  . For details, see [9, Theorem 7]).
. For details, see [9, Theorem 7]).
Theorem 3.6.
Let  be fuzzy function, where
be fuzzy function, where  for each
for each  .
.
(i)If  is (1)-differentiable, then
is (1)-differentiable, then  and
and  are differentiable functions and
are differentiable functions and  .
.
-
(ii)
If
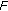 is (2)-differentiable, then
is (2)-differentiable, then 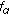 and
and  are differentiable functions and
are differentiable functions and 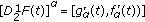 .
.
Proof.
See [11].
Now we introduce definitions for higher-order derivatives based on the selection of derivative type in each step of differentiation. For the sake of convenience, we concentrate on the second-order case.
For a given fuzzy function  , we have two possibilities (Definition 3.2) to obtain the derivative of
, we have two possibilities (Definition 3.2) to obtain the derivative of  ot
ot  :
:  and
and  . Then for each of these two derivatives, we have again two possibilities:
. Then for each of these two derivatives, we have again two possibilities: 
 and
and 
 respectively.
respectively.
Definition 3.7.
Let  and
and  . One says say
. One says say  is
is  -differentiable at
-differentiable at  , if
, if  exists on a neighborhood of
exists on a neighborhood of  as a fuzzy function and it is
as a fuzzy function and it is  -differentiable at
-differentiable at  . The second derivatives of
. The second derivatives of  are denoted by
are denoted by  for
for  .
.
Remark 3.8.
This definition is consistent. For example, if  is
is  and
and  -differentiable simultaneously at
-differentiable simultaneously at  , then
, then  is (1)- and (2)-differentiable around
is (1)- and (2)-differentiable around  . By remark in [9],
. By remark in [9],  is a crisp function in a neighborhood of
is a crisp function in a neighborhood of  .
.
Theorem 3.9.
Let  or
or  be fuzzy functions, where
be fuzzy functions, where  .
.
(i)If  is (1)-differentiable, then
is (1)-differentiable, then  and
and  are differentiable functions and
are differentiable functions and  .
.
-
(ii)
If
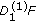 is (2)-differentiable, then
is (2)-differentiable, then 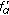 and
and 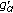 are differentiable functions and
are differentiable functions and 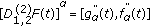 .
. -
(iii)
If
 is (1)-differentiable, then
is (1)-differentiable, then  and
and 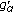 are differentiable functions and
are differentiable functions and 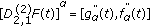 .
. -
(iv)
If
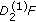 is (2)-differentiable, then
is (2)-differentiable, then  and
and 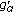 are differentiable functions and
are differentiable functions and  .
.
Proof.
We present the details only for the case (i), since the other cases are analogous.
If  and
and  , we have
, we have

and multiplying by  we have
we have

Similarly, we obtain

Passing to the limit, we have

This completes the proof of the theorem.
Let  be a positive integer number, pursuing the above-cited idea, we write
be a positive integer number, pursuing the above-cited idea, we write  to denote the
to denote the  th-derivatives of
th-derivatives of  at
at  with
with  for
for  . Now we intend to compute the higher derivatives (in generalized differentiability sense) of the
. Now we intend to compute the higher derivatives (in generalized differentiability sense) of the  -difference of two fuzzy functions and the product of a crisp and a fuzzy function.
-difference of two fuzzy functions and the product of a crisp and a fuzzy function.
Lemma 3.10.
If  are
are  th-order generalized differentiable at
th-order generalized differentiable at  in the same case of differentiability, then
in the same case of differentiability, then  is generalized differentiable of order
is generalized differentiable of order  at
at  and
and  . (The sum of two functions is defined pointwise.)
. (The sum of two functions is defined pointwise.)
Proof.
By Definition 3.2 the statement of the lemma follows easily.
Theorem 3.11.
Let  be second-order generalized differentiable such that
be second-order generalized differentiable such that  is (1,1)-differentiable and
is (1,1)-differentiable and  is (2,1)-differentiable or
is (2,1)-differentiable or  is (1,2)-differentiable and
is (1,2)-differentiable and  is (2,2)-differentiable or
is (2,2)-differentiable or  is (2,1)-differentiable and
is (2,1)-differentiable and  is (1,1)-differentiable or
is (1,1)-differentiable or  is (2,2)-differentiable and
is (2,2)-differentiable and  is (1,2)-differentiable on
is (1,2)-differentiable on  . If the
. If the  -difference
-difference  exists for
exists for  then
then  is second-order generalized differentiable and
is second-order generalized differentiable and

for all  .
.
Proof.
We prove the first case and other cases are similar. Since  is (1)-differentiable and
is (1)-differentiable and  is (2)-differentiable on
is (2)-differentiable on  , by [10, Theorem 4],
, by [10, Theorem 4],  is (1)-differentiable and we have
is (1)-differentiable and we have  . By differentiation as (1)-differentiability in Definition 3.2 and using Lemma 3.10, we get
. By differentiation as (1)-differentiability in Definition 3.2 and using Lemma 3.10, we get  is (1,1)-differentiable and we deduce
is (1,1)-differentiable and we deduce

The  -difference of two functions is understood pointwise.
-difference of two functions is understood pointwise.
Theorem 3.12.
Let  and
and  be two differentiable functions (
be two differentiable functions ( is generalized differentiable as in Definition 3.2).
is generalized differentiable as in Definition 3.2).
(i)If  and
and  is (1)-differentiable, then
is (1)-differentiable, then  is (1)-differentiable and
is (1)-differentiable and

-
(ii)
If
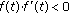 and
and  is (2)-differentiable, then
is (2)-differentiable, then  is (2)-differentiable and
is (2)-differentiable and 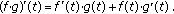 (3.11)
(3.11)
Proof.
See [10].
Theorem 3.13.
Let  and
and  be second-order differentiable functions (
be second-order differentiable functions ( is generalized differentiable as in Definition 3.7).
is generalized differentiable as in Definition 3.7).
(i)If  and
and  is (1,1)-differentiable then
is (1,1)-differentiable then  is (1,1)-differentiable and
is (1,1)-differentiable and

-
(ii)
If
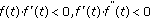 and
and 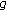 is (2,2)-differentiable then
is (2,2)-differentiable then 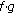 is (2,2)-differentiable and
is (2,2)-differentiable and 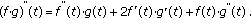 (3.13)
(3.13)
Proof.
We prove (i), and the proof of another case is similar. If  and
and  is (1)-differentiable, then by Theorem 3.12 we have
is (1)-differentiable, then by Theorem 3.12 we have

Now by differentiation as first case in Definition 3.2, since  is (1)-differentiable and
is (1)-differentiable and  then we conclude the result.
then we conclude the result.
Remark 3.14.
By [9, Remark 16], let  and define
and define  by
by  , for all
, for all  . If
. If  is differentiable on
is differentiable on  then
then  is differentiable on
is differentiable on  , with
, with  . By Theorem 3.12, if
. By Theorem 3.12, if  then
then  is (1)-differentiable on
is (1)-differentiable on  . Also if
. Also if  then
then  is (2)-differentiable on
is (2)-differentiable on  . If
. If  , by [9, Theorem 10], we have
, by [9, Theorem 10], we have  . We can extend this result to second-order differentiability as follows.
. We can extend this result to second-order differentiability as follows.
Theorem 3.15.
Let  be twice differentiable on
be twice differentiable on  ,
,  and define
and define  by
by  , for all
, for all  .
.
(i)If  and
and  then
then  is (1,1)-differentiable and its second derivative,
is (1,1)-differentiable and its second derivative,  is
is  ,
,
-
(ii)
If
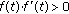 and
and 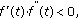 then
then  is (1,2)-differentiable with
is (1,2)-differentiable with  ,
, -
(iii)
If
 and
and 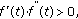 then
then  is (2,1)-differentiable with
is (2,1)-differentiable with 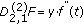 ,
, -
(iv)
If
 and
and 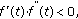 then
then 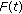 is (2,2)-differentiable with
is (2,2)-differentiable with 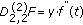 .
.
Proof.
Cases (i) and (iv) follow from Theorem 3.13. To prove (ii), since  , by Remark 3.14,
, by Remark 3.14,  is (1)-differentiable and we have
is (1)-differentiable and we have  on
on  . Also, since
. Also, since  , then
, then  is (2)-differentiable and we conclude the result. Case (iii) is similar to previous one.
is (2)-differentiable and we conclude the result. Case (iii) is similar to previous one.
Example 3.16.
If  is a fuzzy number and
is a fuzzy number and  where
where

is crisp second-order polynomial, then for

we have the following
(i)for :
:  and
and  then by (iv),
then by (iv),  is (2-2)-differentiable and its second derivative,
is (2-2)-differentiable and its second derivative,  is
is  ,
,
(ii)for :
:  and
and  then by (ii),
then by (ii),  is (1-2)-differentiable with
is (1-2)-differentiable with  ,
,
(iii)for :
:  and
and  then by (iii),
then by (iii),  is (2-1)-differentiable and
is (2-1)-differentiable and  ,
,
(iv)for :
:  and
and  then by (i),
then by (i),  is (1-1)-differentiable and
is (1-1)-differentiable and  ,
,
(v)for : we have
: we have  , then by [9, Theorem 10] we have
, then by [9, Theorem 10] we have  , again by applying this theorem, we get
, again by applying this theorem, we get 
4. Second-Order Fuzzy Differential Equations
In this section, we study the fuzzy initial value problem for a second-order linear fuzzy differential equation:

where  ,
,  and
and  is a continuous fuzzy function on some interval
is a continuous fuzzy function on some interval  . The interval
. The interval  can be
can be  for some
for some  or
or  . In this paper, we suppose
. In this paper, we suppose  Our strategy of solving (4.1) is based on the selection of derivative type in the fuzzy differential equation. We first give the following definition for the solutions of (4.1).
Our strategy of solving (4.1) is based on the selection of derivative type in the fuzzy differential equation. We first give the following definition for the solutions of (4.1).
Definition 4.1.
Let  be a fuzzy function and
be a fuzzy function and  One says
One says  is an
is an  -solution for problem (4.1) on
-solution for problem (4.1) on  , if
, if 
 exist on
exist on  and
and  .
.
Let  be an
be an  -solution for (4.1). To find it, utilizing Theorems 3.6 and 3.9 and considering the initial values, we can translate problem (4.1) to a system of second-order linear ordinary differential equations hereafter, called corresponding
-solution for (4.1). To find it, utilizing Theorems 3.6 and 3.9 and considering the initial values, we can translate problem (4.1) to a system of second-order linear ordinary differential equations hereafter, called corresponding  -system for problem (4.1).
-system for problem (4.1).
Therefore, four ODEs systems are possible for problem (4.1), as follows:
 -system
-system

 -system
-system

 -system
-system

 -system
-system

Theorem 4.2.
Let  and
and  be an
be an  -solution for problem (4.1) on
-solution for problem (4.1) on  . Then
. Then  and
and  solve the associated
solve the associated  -systems.
-systems.
Proof.
Suppose  is the
is the  -solution of problem (4.1). According to the Definition 4.1, then
-solution of problem (4.1). According to the Definition 4.1, then  and
and  exist and satisfy problem (4.1). By Theorems 3.6 and 3.9 and substituting
exist and satisfy problem (4.1). By Theorems 3.6 and 3.9 and substituting  and their derivatives in problem (4.1), we get the
and their derivatives in problem (4.1), we get the  -system corresponding to
-system corresponding to  -solution. This completes the proof.
-solution. This completes the proof.
Theorem 4.3.
Let  and
and  and
and  solve the
solve the  -system on
-system on  for every
for every  . Let
. Let  . If
. If  has valid level sets on
has valid level sets on  and
and  exists, then
exists, then  is an
is an  -solution for the fuzzy initial value problem (4.1).
-solution for the fuzzy initial value problem (4.1).
Proof.
Since  is (
is ( )-differentiable fuzzy function, by Theorems 3.6 and 3.9 we can compute
)-differentiable fuzzy function, by Theorems 3.6 and 3.9 we can compute  and
and  according to
according to 
 . Due to the fact that
. Due to the fact that  solve
solve  -system, from Definition 4.1, it comes that
-system, from Definition 4.1, it comes that  is an
is an  -solution for (4.1).
-solution for (4.1).
The previous theorems illustrate the method to solve problem (4.1). We first choose the type of solution and translate problem (4.1) to a system of ordinary differential equations. Then, we solve the obtained ordinary differential equations system. Finally we find such a domain in which the solution and its derivatives have valid level sets and using Stacking Theorem [5] we can construct the solution of the fuzzy initial value problem (4.1).
Remark 4.4.
We see that the solution of fuzzy differential equation (4.1) depends upon the selection of derivatives. It is clear that in this new procedure, the unicity of the solution is lost, an expected situation in the fuzzy context. Nonetheless, we can consider the existence of four solutions as shown in the following examples.
Example 4.5.
Let us consider the following second-order fuzzy initial value problem

where  are the triangular fuzzy number having
are the triangular fuzzy number having  -level sets
-level sets 
If  is (1,1)-solution for the problem, then
is (1,1)-solution for the problem, then

and they satisfy (1,1)-system associated with (4.1). On the other hand, by ordinary differential theory, the corresponding (1,1)-system has only the following solution:

We see that  are valid level sets for
are valid level sets for  and
and

By Theorem 3.15,  is (1,1)-differentiable for
is (1,1)-differentiable for  . Therefore,
. Therefore,  defines a (1,1)-solution for
defines a (1,1)-solution for  .
.
For (1,2)-solution, we get the following solutions for (1,2)-system:

where  has valid level sets for
has valid level sets for  How ever-also
How ever-also  where
where  is (1,2)-differentiable. Then
is (1,2)-differentiable. Then  gives us a (1,2)-solution on
gives us a (1,2)-solution on  .
.
(2,1)-system yields

where  has valid level sets for
has valid level sets for  We can see
We can see  is a (2,1)-solution on
is a (2,1)-solution on 
Finally, (2-2)-system gives

where  has valid level sets for all
has valid level sets for all  and defines a (2,2)-solution on
and defines a (2,2)-solution on  .
.
Then we have an example of a second-order fuzzy initial value problem with four different solutions.
Example 4.6.
Consider the fuzzy initial value problem:

where  is the fuzzy number having
is the fuzzy number having  -level sets
-level sets  and
and 
To find (1,1)-solution, we have

where  has valid level sets for
has valid level sets for  and
and  . From Theorem 3.15,
. From Theorem 3.15,  is (1,2)-differentiable on
is (1,2)-differentiable on  , then by Remark 3.8,
, then by Remark 3.8,  is not
is not  -differentiable on
-differentiable on  . Hence, no (1,1)-solution exists for
. Hence, no (1,1)-solution exists for  .
.
For (1,2)-solutions we deduce

we see that  has valid level sets and is (1,1)-differentiable for
has valid level sets and is (1,1)-differentiable for  . Since the (1,2)-system has only the above solution, then (1,2)-solution does not exist.
. Since the (1,2)-system has only the above solution, then (1,2)-solution does not exist.
For (2,1)-solutions we get

we see that the fuzzy function  has valid level sets for
has valid level sets for  and define a (2,1)-solution for the problem on
and define a (2,1)-solution for the problem on 
Finally, to find (2,2)-solution, we find

that  has valid level sets for
has valid level sets for  and
and  is (2,2)-differentiable on
is (2,2)-differentiable on  .
.
We then have a linear fuzzy differential equation with initial condition and two solutions.
5. Higher-Order Fuzzy Differential Equations
Selecting different types of derivatives, we get several solutions to fuzzy initial value problem for second-order fuzzy differential equations. Theorem 4.2 has a crucial role in our strategy. To extend the results to  th-order fuzzy differential equation, we can follow the proof of Theorem 4.2 to get the same results for derivatives of higher order. Therefore, we can extend the presented argument for second-order fuzzy differential equation to
th-order fuzzy differential equation, we can follow the proof of Theorem 4.2 to get the same results for derivatives of higher order. Therefore, we can extend the presented argument for second-order fuzzy differential equation to  th-order. Under generalized derivatives, we would expect at most
th-order. Under generalized derivatives, we would expect at most  solutions for an
solutions for an  th-order fuzzy differential equation by choosing the different types of derivatives.
th-order fuzzy differential equation by choosing the different types of derivatives.
References
Kandel A, Byatt WJ: Fuzzy differential equations. Proceedings of the International Conference on Cybernetics and Society, 1978, Tokyo, Japan 1213–1216.
Kandel A, Byatt WJ: Fuzzy processes. Fuzzy Sets and Systems 1980, 4(2):117–152. 10.1016/0165-0114(80)90032-9
Buckley JJ, Feuring T: Fuzzy differential equations. Fuzzy Sets and Systems 2000, 110(1):43–54. 10.1016/S0165-0114(98)00141-9
Puri ML, Ralescu DA: Differentials of fuzzy functions. Journal of Mathematical Analysis and Applications 1983, 91(2):552–558. 10.1016/0022-247X(83)90169-5
Kaleva O: Fuzzy differential equations. Fuzzy Sets and Systems 1987, 24(3):301–317. 10.1016/0165-0114(87)90029-7
Diamond P, Kloeden P: Metric Spaces of Fuzzy Sets. World Scientific, Singapore; 1994:x+178.
Hüllermeier E: An approach to modelling and simulation of uncertain dynamical systems. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 1997, 5(2):117–137. 10.1142/S0218488597000117
Bede B, Gal SG: Almost periodic fuzzy-number-valued functions. Fuzzy Sets and Systems 2004, 147(3):385–403. 10.1016/j.fss.2003.08.004
Bede B, Gal SG: Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy Sets and Systems 2005, 151(3):581–599. 10.1016/j.fss.2004.08.001
Bede B, Rudas IJ, Bencsik AL: First order linear fuzzy differential equations under generalized differentiability. Information Sciences 2007, 177(7):1648–1662. 10.1016/j.ins.2006.08.021
Chalco-Cano Y, Román-Flores H: On new solutions of fuzzy differential equations. Chaos, Solitons & Fractals 2008, 38(1):112–119. 10.1016/j.chaos.2006.10.043
Georgiou DN, Nieto JJ, Rodríguez-López R: Initial value problems for higher-order fuzzy differential equations. Nonlinear Analysis: Theory, Methods & Applications 2005, 63(4):587–600. 10.1016/j.na.2005.05.020
Buckley JJ, Feuring T: Fuzzy initial value problem for
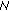 th-order linear differential equations. Fuzzy Sets and Systems 2001, 121(2):247–255. 10.1016/S0165-0114(00)00028-2
th-order linear differential equations. Fuzzy Sets and Systems 2001, 121(2):247–255. 10.1016/S0165-0114(00)00028-2Chang SSL, Zadeh LA: On fuzzy mapping and control. IEEE Transactions on Systems Man Cybernetics 1972, 2: 30–34.
Dubois D, Prade H: Towards fuzzy differential calculus—part III: differentiation. Fuzzy Sets and Systems 1982, 8(3):225–233. 10.1016/S0165-0114(82)80001-8
Goetschel R Jr., Voxman W: Elementary fuzzy calculus. Fuzzy Sets and Systems 1986, 18(1):31–43. 10.1016/0165-0114(86)90026-6
Lakshmikantham V, Nieto JJ: Differential equations in metric spaces: an introduction and an application to fuzzy differential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2003, 10(6):991–1000.
Acknowledgments
We thank Professor J. J. Nieto for his valuable remarks which improved the paper. This research is supported by a grant from University of Tabriz.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Khastan, A., Bahrami, F. & Ivaz, K. New Results on Multiple Solutions for  th-Order Fuzzy Differential Equations under Generalized Differentiability.
Bound Value Probl 2009, 395714 (2009). https://doi.org/10.1155/2009/395714
th-Order Fuzzy Differential Equations under Generalized Differentiability.
Bound Value Probl 2009, 395714 (2009). https://doi.org/10.1155/2009/395714
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/395714
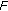 is (2)-differentiable, then
is (2)-differentiable, then 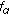 and
and  are differentiable functions and
are differentiable functions and 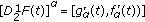 .
.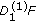 is (2)-differentiable, then
is (2)-differentiable, then 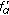 and
and 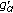 are differentiable functions and
are differentiable functions and 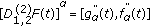 .
. is (1)-differentiable, then
is (1)-differentiable, then  and
and 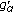 are differentiable functions and
are differentiable functions and 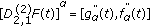 .
.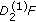 is (2)-differentiable, then
is (2)-differentiable, then  and
and 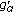 are differentiable functions and
are differentiable functions and  .
.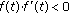 and
and  is (2)-differentiable, then
is (2)-differentiable, then  is (2)-differentiable and
is (2)-differentiable and 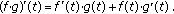
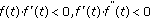 and
and 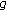 is (2,2)-differentiable then
is (2,2)-differentiable then 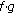 is (2,2)-differentiable and
is (2,2)-differentiable and 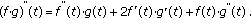
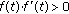 and
and 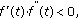 then
then  is (1,2)-differentiable with
is (1,2)-differentiable with  ,
, and
and 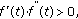 then
then  is (2,1)-differentiable with
is (2,1)-differentiable with 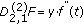 ,
, and
and 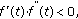 then
then 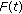 is (2,2)-differentiable with
is (2,2)-differentiable with 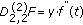 .
. th-order linear differential equations. Fuzzy Sets and Systems 2001, 121(2):247–255. 10.1016/S0165-0114(00)00028-2
th-order linear differential equations. Fuzzy Sets and Systems 2001, 121(2):247–255. 10.1016/S0165-0114(00)00028-2