- Research Article
- Open access
- Published:
The Problem of Scattering by a Mixture of Cracks and Obstacles
Boundary Value Problems volume 2009, Article number: 524846 (2009)
Abstract
Consider the scattering of an electromagnetic time-harmonic plane wave by an infinite cylinder having an open crack  and a bounded domain
and a bounded domain  in
in  as cross section. We assume that the crack
as cross section. We assume that the crack  is divided into two parts, and one of the two parts is (possibly) coated on one side by a material with surface impedance
is divided into two parts, and one of the two parts is (possibly) coated on one side by a material with surface impedance  . Different boundary conditions are given on
. Different boundary conditions are given on  and
and  . Applying potential theory, the problem can be reformulated as a boundary integral system. We obtain the existence and uniqueness of a solution to the system by using Fredholm theory.
. Applying potential theory, the problem can be reformulated as a boundary integral system. We obtain the existence and uniqueness of a solution to the system by using Fredholm theory.
1. Introduction
Crack detection is a problem in nondestructive testing of materials which has been often addressed in literature and more recently in the context of inverse problems. Early works on the direct and inverse scattering problem for cracks date back to 1995 in [1] by Kress. In that paper, Kress considered the direct and inverse scattering problem for a perfectly conducting crack and used Newton's method to reconstruct the shape of the crack from a knowledge of the far-field pattern. In 1997, M nch considered the same scattering problem for sound-hard crack [2], and in the same year, Alves and Ha Duong discussed the scattering problem but for flat cracks in [3]. Later in 2000, Kress's work was continued by Kirsch and Ritter in [4] who used the factorization method to reconstruct the shape of the crack from the knowledge of the far-field pattern. In 2003, Cakoni and Colton in [5] considered the direct and inverse scattering problem for cracks which (possibly) coated on one side by a material with surface impedance
nch considered the same scattering problem for sound-hard crack [2], and in the same year, Alves and Ha Duong discussed the scattering problem but for flat cracks in [3]. Later in 2000, Kress's work was continued by Kirsch and Ritter in [4] who used the factorization method to reconstruct the shape of the crack from the knowledge of the far-field pattern. In 2003, Cakoni and Colton in [5] considered the direct and inverse scattering problem for cracks which (possibly) coated on one side by a material with surface impedance  . Later in 2008, Lee considered an inverse scattering problem from an impedance crack and tried to recover impedance function from the far field pattern in [6]. However, studying an inverse problem always requires a solid knowledge of the corresponding direct problem. Therefore, in the following we just consider the direct scattering problem for a mixture of a crack
. Later in 2008, Lee considered an inverse scattering problem from an impedance crack and tried to recover impedance function from the far field pattern in [6]. However, studying an inverse problem always requires a solid knowledge of the corresponding direct problem. Therefore, in the following we just consider the direct scattering problem for a mixture of a crack  and a bounded domain
and a bounded domain  , and the corresponding inverse scattering problem can be considered by similar methods in [1, 2, 4–12] and the reference therein.
, and the corresponding inverse scattering problem can be considered by similar methods in [1, 2, 4–12] and the reference therein.
Briefly speaking, in this paper we consider the scattering of an electromagnetic time-harmonic plane wave by an infinite cylinder having an open crack  and a bounded domain
and a bounded domain  in
in  as cross section. We assume that the cylinder is (possibly) partially coated on one side by a material with surface impedance
as cross section. We assume that the cylinder is (possibly) partially coated on one side by a material with surface impedance  . This corresponds to the situation when the boundary or more generally a portion of the boundary is coated with an unknown material in order to avoid detection. Assuming that the electric field is polarized in the
. This corresponds to the situation when the boundary or more generally a portion of the boundary is coated with an unknown material in order to avoid detection. Assuming that the electric field is polarized in the  mode, this leads to a mixed boundary value problem for the Helmholtz equation defined in the exterior of a mixture in
mode, this leads to a mixed boundary value problem for the Helmholtz equation defined in the exterior of a mixture in  .
.
Our aim is to establish the existence and uniqueness of a solution to this direct scattering problem. As is known, the method of boundary integral equations has widely applications to various direct and inverse scattering problems (see [13–17] and the reference therein). A few authors have applied such method to study the scattering problem with mixture of cracks and obstacles. In the following, we will use the method of boundary integral equations and Fredholm theory to obtain the existence and uniqueness of a solution. The difficult thing is to prove the corresponding boundary integral operator  which is a Fredholm operator with index zero since the boundary is a mixture and we have complicated boundary conditions.
which is a Fredholm operator with index zero since the boundary is a mixture and we have complicated boundary conditions.
The outline of the paper is as follows. In Section 2, the direct scattering problem is considered, and we will establish uniqueness to the problem and reformulate the problem as a boundary integral system by using single- and double-layer potentials. The existence and uniqueness of a solution to the corresponding boundary integral system will be given in Section 3. The potential theory and Fredholm theory will be used to prove our main results.
2. Boundary Integral Equations of the Direct Scattering Problem
Consider the scattering of time-harmonic electromagnetic plane waves from an infinite cylinder with a mixture of an open crack  and a bounded domain
and a bounded domain  in
in  as cross section. For further considerations, we suppose that
as cross section. For further considerations, we suppose that  has smooth boundary
has smooth boundary  (e.g.,
(e.g.,  ), and the crack
), and the crack  (smooth) can be extended to an arbitrary smooth, simply connected, closed curve
(smooth) can be extended to an arbitrary smooth, simply connected, closed curve  enclosing a bounded domain
enclosing a bounded domain  such that the normal vector
such that the normal vector  on
on  coincides with the outward normal vector on
coincides with the outward normal vector on  which we again denote by
which we again denote by  . The bounded domain
. The bounded domain  is located inside the domain
is located inside the domain  , and
, and  .
.
In the whole paper, we assume that  and
and  .
.
Suppose that

where  is an injective piecewise
is an injective piecewise  function. We denote the outside of
function. We denote the outside of  with respect to the chosen orientation by
with respect to the chosen orientation by  and the inside by
and the inside by  . Here we suppose that the
. Here we suppose that the  is divided into two parts
is divided into two parts  and
and  and consider the electromagnetic field E-polarized. Different boundary conditions on
and consider the electromagnetic field E-polarized. Different boundary conditions on  ,
,  and
and  lead to the following problem:
lead to the following problem:

where  for
for  and
and  for
for  . The total field
. The total field  is decomposed into the given incident field
is decomposed into the given incident field  , and the unknown scattered field
, and the unknown scattered field  which is required to satisfy the Sommerfeld radiation condition
which is required to satisfy the Sommerfeld radiation condition

uniformly in  with
with  .
.
We recall some usual Sobolev spaces and some trace spaces on  in the following.
in the following.
Let  be a piece of the boundary. Use
be a piece of the boundary. Use  and
and  to denote the usual Sobolev spaces,
to denote the usual Sobolev spaces,  is the trace space, and we define
is the trace space, and we define

Just consider the scattered field  , then (2.2) and (2.3) are a special case of the following problem.
, then (2.2) and (2.3) are a special case of the following problem.
Given  ,
,  ,
,  and
and  find
find  such that
such that

and  is required to satisfy the Sommerfeld radiation condition (2.3). For simplicity, we assume that
is required to satisfy the Sommerfeld radiation condition (2.3). For simplicity, we assume that  and
and  .
.
Theorem 2.1.
The problems (2.5) and (2.3) have at most one solution.
Proof.
Let  be a solution to the problem (2.5) with
be a solution to the problem (2.5) with  , we want to show that
, we want to show that  in
in  .
.
Suppose that  (with boundary
(with boundary  ) is a sufficiently large ball which contains the domain
) is a sufficiently large ball which contains the domain  . Obviously, to the Helmholtz equation in (2.5), the solution
. Obviously, to the Helmholtz equation in (2.5), the solution  satisfies the following transmission boundary conditions on the complementary part
satisfies the following transmission boundary conditions on the complementary part  of
of  :
:

where " " denote the limit approaching
" denote the limit approaching  from outside and inside
from outside and inside  , respectively. Applying Green's formula for
, respectively. Applying Green's formula for  and
and  in
in  and
and  , we have
, we have

where  is directed into the exterior of the corresponding domain.
is directed into the exterior of the corresponding domain.
Using boundary conditions on  ,
,  and the above transmission boundary condition (2.6), we have
and the above transmission boundary condition (2.6), we have

Hence

So, from [13, Theorem  ] and a unique continuation argument we obtain that
] and a unique continuation argument we obtain that  in
in  .
.
We use  and
and  to denote the jump of
to denote the jump of  and
and  across the crack
across the crack  , respectively. Then we have the following.
, respectively. Then we have the following.
Lemma 2.2.
If  is a solution of (2.5) and (2.3), then
is a solution of (2.5) and (2.3), then  and
and  .
.
The proof of this lemma can be found in [11].
We are now ready to prove the existence of a solution to the above scattering problem by using an integral equation approaching. For  , by Green representation formula
, by Green representation formula

and for 

where

is the fundamental solution to the Helmholtz equation in  , and
, and  is a Hankel function of the first kind of order zero.
is a Hankel function of the first kind of order zero.
By making use of the known jump relationships of the single- and double-layer potentials across the boundary  (see [5, 11]) and approaching the boundary
(see [5, 11]) and approaching the boundary  from inside
from inside  , we obtain (for
, we obtain (for  )
)


where  ,
,  ,
,  , and
, and  are boundary integral operators:
are boundary integral operators:

defined by (for  )
)

Similarly, approaching the boundary  from inside
from inside  we obtain (for
we obtain (for  )
)


From (2.13)–(2.18), we have


Restrict  on
on  , from (2.19) we have
, from (2.19) we have

where  means a restriction to
means a restriction to  .
.
Define

Then zero extend  ,
,  , and
, and  to the whole
to the whole  in the following:
in the following:

By using the boundary conditions in (2.5), we rewrite (2.21) as

where

Furthermore, we modify (2.24) as

where the operator  is the operator applied to a function with
is the operator applied to a function with  and evaluated on
and evaluated on  , with analogous definition for
, with analogous definition for  ,
,  , and
, and  . We have mapping properties (see [5, 11])
. We have mapping properties (see [5, 11])

Again from (2.13)–(2.18), restricting  to boundary
to boundary  we have
we have

or

Like previous, define

Then we can rewrite (2.29) as

where

Similar to (2.26), we modify (2.31) as

and we have mapping properties:

Combining (2.13) and (2.14),


Using (2.17) and (2.18),

Then using (2.36),

From (2.29), we have

Restricting (2.38) to  and using (2.39), we modify (2.38) as
and using (2.39), we modify (2.38) as

where

for  .
.
Define

and using the notation in previous, we can rewrite (2.40) as

or

where the operators  ,
,  , and
, and  are restriction operators (see (2.29)). As before, we have mapping properties:
are restriction operators (see (2.29)). As before, we have mapping properties:

By using Green formula and approaching the boundary  from inside
from inside  we obtain (for
we obtain (for  )
)

The last term in (2.46) can be reformulated as

Since  and
and  in (2.47), we have the following result (see [13]).
in (2.47), we have the following result (see [13]).
Lemma 2.3.
By using Green formula and the Sommerfeld radiation condition (2.3), one obtains

Proof.
Denote by  a sufficiently large ball with radius
a sufficiently large ball with radius  containing
containing  and use Green formula inside
and use Green formula inside  . Furthermore noticing
. Furthermore noticing  ,
,  , and the Sommerfeld radiation condition (2.3), we can prove this lemma.
, and the Sommerfeld radiation condition (2.3), we can prove this lemma.
Combining (2.46), (2.47), and Lemma 2.3 and restricting  to
to  we have
we have

where

Define

and then we can rewrite (2.49) as

Similarly,  and
and  are restriction operators as before, and we have mapping properties:
are restriction operators as before, and we have mapping properties:

Combining (2.52), (2.26), (2.33), and (2.44), we have

If we define

then (2.54) can be rewritten as a boundary integral system:

Remark 2.4.
If the above system (2.56) has a unique solution, our problem (2.5) with (2.3) will have a unique solution (see [13, 14]).
3. Existence and Uniqueness
Based on the Fredholm theory, we show the existence and uniqueness of a solution to the integral system (2.56).
Define

and its dual space

Theorem 3.1.
The operator  maps
maps  continuously into
continuously into  and is Fredholm with index zero.
and is Fredholm with index zero.
Proof.
As is known, the operator  is positive and bounded below up to a compact perturbation (see [18]); that is, there exists a compact operator
is positive and bounded below up to a compact perturbation (see [18]); that is, there exists a compact operator

such that

where  denote the duality between
denote the duality between  and
and  .
.
For convenience, in the following discussion we define

Similarly, the operators  and
and  are positive and bounded below up to compact perturbations (see [18]), that is, there exist compact operators
are positive and bounded below up to compact perturbations (see [18]), that is, there exist compact operators

such that

Define  and
and  , then
, then  and
and  are bounded below up and positive.
are bounded below up and positive.
Take  , and let
, and let  ,
,  , and
, and  be the extension by zero to
be the extension by zero to  of
of  ,
,  , and
, and  respectively.
respectively.
Denote  .
.
It is easy to check that the operators  ,
,  ,
,  ,
,  ,
,  , and
, and  are compact operators, and then we can rewrite
are compact operators, and then we can rewrite  as the following:
as the following:

with

where  is compact and
is compact and  defines a sesquilinear form, that is,
defines a sesquilinear form, that is,

Here  denotes the scalar product on
denotes the scalar product on  or
or  defined by
defined by  or
or  , and
, and  is the scalar product on
is the scalar product on  (
( ).
).
By properties of the operators  ,
,  , and
, and  , we have
, we have

Similarly,

So the operator  is coercive, that is,
is coercive, that is,

whence the operator  is Fredholm with index zero.
is Fredholm with index zero.
Theorem 3.2.
The operator  has a trivial kernel if
has a trivial kernel if  is not Dirichlet eigenvalue of the Laplace operator in
is not Dirichlet eigenvalue of the Laplace operator in  .
.
Proof.
In this part, we show that  . To this end let
. To this end let  be a solution of the homogeneous system
be a solution of the homogeneous system  , and we want to prove that
, and we want to prove that  .
.
However,  means that
means that

Define a potential

where  ,
,  and
and  have the same meaning as before and
have the same meaning as before and

This potential  satisfies Helmholtz equation in
satisfies Helmholtz equation in  and the Sommerfeld radiation condition (see [13, 14]).
and the Sommerfeld radiation condition (see [13, 14]).
Considering the potential  inside
inside  and approaching the boundary
and approaching the boundary  (
( ), we have
), we have

and (3.14) implies that

Similarly, considering the potential  inside
inside  and approaching the boundary
and approaching the boundary  (
( ), then restricting
), then restricting  to the partial boundary
to the partial boundary  :
:

and restricting  to the partial boundary
to the partial boundary  , we have
, we have

Now, we consider the potential  in the region
in the region  and approach the boundary
and approach the boundary  (
( ), and then restricting
), and then restricting  to the partial boundary
to the partial boundary  , similar to (3.19), we have
, similar to (3.19), we have

Refering to (3.20),

Combining (3.22), from (3.14) we have

From (3.18)–(3.23), the potential  satisfies the following boundary value problem:
satisfies the following boundary value problem:

and the Sommerfeld radiation condition:

uniformly in  with
with  .
.
The uniqueness result Theorem 2.1 in Section 2 implies that

Notice that  is not Dirichlet eigenvalue of the Laplace operator in
is not Dirichlet eigenvalue of the Laplace operator in  , and so
, and so

Therefore, the well-known jump relationships (see [13, 14]) imply that

So we complete the proof of the theorem.
Combining Theorems 3.1 and 3.2, we have the following
Theorem 3.3.
The boundary integral system (2.56) has a unique solution.
Remark 3.4.
If we remove the condition that " is not Dirichlet eigenvalue of the Laplace operator in
is not Dirichlet eigenvalue of the Laplace operator in  ," instead of it by the assumption that Im
," instead of it by the assumption that Im  , then Theorem 2.1 in Section 2 and Theorem 3.3 in Section 3 are also true.
, then Theorem 2.1 in Section 2 and Theorem 3.3 in Section 3 are also true.
References
Kress R: Frechet differentiability of the far field operator for scattering from a crack. Journal of Inverse and Ill-Posed Problems 1995, 3(4):305–313. 10.1515/jiip.1995.3.4.305
Mönch L: On the inverse acoustic scattering problem by an open arc: the sound-hard case. Inverse Problems 1997, 13(5):1379–1392. 10.1088/0266-5611/13/5/017
Alves CJS, Ha-Duong T: On inverse scattering by screens. Inverse Problems 1997, 13(5):1161–1176. 10.1088/0266-5611/13/5/004
Kirsch A, Ritter S: A linear sampling method for inverse scattering from an open arc. Inverse Problems 2000, 16(1):89–105. 10.1088/0266-5611/16/1/308
Cakoni F, Colton D: The linear sampling method for cracks. Inverse Problems 2003, 19(2):279–295. 10.1088/0266-5611/19/2/303
Lee K-M: Inverse scattering problem for an impedance crack. Wave Motion 2008, 45(3):254–263. 10.1016/j.wavemoti.2007.06.002
Ammari H, Bao G, Wood AW: An integral equation method for the electromagnetic scattering from cavitys. Mathematical Methods in the Applied Sciences 2000, 23(12):1057–1072. 10.1002/1099-1476(200008)23:12<1057::AID-MMA151>3.0.CO;2-6
Cheng J, Hon YC, Yamamoto M: Conditional stability estimation for an inverse boundary problem with non-smooth boundary in
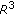 . Transactions of the American Mathematical Society 2001, 353(10):4123–4138. 10.1090/S0002-9947-01-02758-1
. Transactions of the American Mathematical Society 2001, 353(10):4123–4138. 10.1090/S0002-9947-01-02758-1Hohage T: Convergence rates of a regularized Newton method in sound-hard inverse scattering. SIAM Journal on Numerical Analysis 1998, 36(1):125–142. 10.1137/S0036142997327750
Coyle J, Monk P: Scattering of time-harmonic electromagnetic waves by anisotropic inhomogeneous scatterers or impenetrable obstacles. SIAM Journal on Numerical Analysis 2000, 37(5):1590–1617. 10.1137/S0036142998349515
Cakoni F, Colton D, Monk P: The direct and inverse scattering problems for partially coated obstacles. Inverse Problems 2001, 17(6):1997–2015. 10.1088/0266-5611/17/6/327
Potthast R: On the convergence of a new Newton-type method in inverse scattering. Inverse Problems 2001, 17(5):1419–1434. 10.1088/0266-5611/17/5/312
Colton DL, Kress R: Inverse Acoustic and Electromagnetic Scattering Theory. Springer, Berlin, Germany; 1998.
Colton DL, Kress R: Integral Equation Methods in Scattering Theory, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1983:xii+271.
Chandler-Wilde SN, Zhang B: A uniqueness result for scattering by infinite rough surfaces. SIAM Journal on Applied Mathematics 1998, 58(6):1774–1790. 10.1137/S0036139996309722
Elschner J, Hinder R, Penzel F, Schmidt G: Existence, uniqueness and regularity for solutions of the conical diffraction problem. Mathematical Models & Methods in Applied Sciences 2000, 10(3):317–341. 10.1142/S0218202500000197
Ramm AG: Uniqueness theorems for inverse obstacle scattering problems in Lipschitz domains. Applicable Analysis 1995, 59(1–4):377–383.
McLean W: Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press, Cambridge, UK; 2000:xiv+357.
Acknowledgment
This research is supported by NSFC Grant no. 10871080, Laboratory of Nonlinear Analysis of CCNU, COCDM of CCNU.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yan, G. The Problem of Scattering by a Mixture of Cracks and Obstacles. Bound Value Probl 2009, 524846 (2009). https://doi.org/10.1155/2009/524846
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/524846
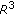 . Transactions of the American Mathematical Society 2001, 353(10):4123–4138. 10.1090/S0002-9947-01-02758-1
. Transactions of the American Mathematical Society 2001, 353(10):4123–4138. 10.1090/S0002-9947-01-02758-1