- Research Article
- Open access
- Published:
Multiplicity of Positive and Nodal Solutions for Nonhomogeneous Elliptic Problems in Unbounded Cylinder Domains
Boundary Value Problems volume 2009, Article number: 687385 (2009)
Abstract
We show that if  and
and  satisfy some suitable conditions, then the Dirichlet problem
satisfy some suitable conditions, then the Dirichlet problem  in
in  has a solution that changes sign in
has a solution that changes sign in  , in addition to two positive solutions where
, in addition to two positive solutions where  is an unbounded cylinder domain in
is an unbounded cylinder domain in  .
.
1. Introduction
Throughout this paper, let  be the generic point of
be the generic point of  with
with  ,
,  , where
, where

In this paper, we study the multiplicity results of both positive and nodal solutions for the nonhomogeneous elliptic problems

where  is a bounded smooth domain,
is a bounded smooth domain,  is a smooth unbounded cylinder domain in
is a smooth unbounded cylinder domain in  .
.
It is assumed that  and
and  satisfy the following assumptions:
satisfy the following assumptions:
(a 1) is continuous and
is continuous and  on
on  and
and

(f 1) ;
;
(f 2) in which we defined
in which we defined

(f 3)there exist positive constants  such that
such that

where  is the first positive eigenvalue of the Dirichlet problem
is the first positive eigenvalue of the Dirichlet problem  in
in  .
.
For the homogeneous case, that is,  , Zhu [1] has established the existence of a positive solution and a nodal solution of problem (1.2) in
, Zhu [1] has established the existence of a positive solution and a nodal solution of problem (1.2) in  provided
provided  satisfies
satisfies  in
in  and
and  as
as  for some positive constants
for some positive constants  and
and  . More recently, Hsu [2] extended the results of Zhu [1] with
. More recently, Hsu [2] extended the results of Zhu [1] with  to an unbounded cylinder
to an unbounded cylinder  . Let us recall that, by a nodal solution we mean the solution of problem (1.2) with change of sign.
. Let us recall that, by a nodal solution we mean the solution of problem (1.2) with change of sign.
For the nonhomogeneous case ( ),Adachi and Tanaka [3] have showed that problem (1.2) has at least four positive solutions in
),Adachi and Tanaka [3] have showed that problem (1.2) has at least four positive solutions in  for
for  and
and  satisfy some suitable conditions, but we place particular emphasis on the existence of nodal solutions. More recently, Chen [4] considered the multiplicity results of both positive and nodal solutions of problem (1.2) in
satisfy some suitable conditions, but we place particular emphasis on the existence of nodal solutions. More recently, Chen [4] considered the multiplicity results of both positive and nodal solutions of problem (1.2) in  . She has showed that problem (1.2) has at least two positive solutions and one nodal solution in
. She has showed that problem (1.2) has at least two positive solutions and one nodal solution in  when
when  and
and  satisfy some suitable assumptions.
satisfy some suitable assumptions.
In the present paper, motivated by [4] we extend and improve the paper by Chen [4]. We will deal with unbounded cylinder domains instead of the entire space and also obtain the same results as in [4]. Our arguments are similar to those in [5, 6], which are based on Ekeland's variational principle [7].
Now, we state our main results.
Theorem 1.1.
Assume  hold and
hold and  satisfies assumption
satisfies assumption  .
.
(a2)there exist positive constants  such that
such that

Then problem (1.2) has at least two positive solutions  and
and  in
in  . Furthermore,
. Furthermore,  and
and  satisfy
satisfy  , and
, and  is a local minimizer of
is a local minimizer of  where
where  is the energy functional of problem (1.2).
is the energy functional of problem (1.2).
Theorem 1.2.
Assume  hold and
hold and  satisfies assumption
satisfies assumption  .
.
(a3)there exist positive constants  , and
, and  such that
such that

Then problem (1.2) has a nodal solution in  in addition to two positive solutions
in addition to two positive solutions  and
and  .
.
For the case  , we also have obtained the same results as in Theorems 1.1 and 1.2.
, we also have obtained the same results as in Theorems 1.1 and 1.2.
Theorem 1.3.
Assume  hold and
hold and  satisfies assumption
satisfies assumption  .
.
(a2)there exist positive constants  such that
such that

Then problem (1.2) has at least two positive solutions  and
and  in
in  . Furthermore,
. Furthermore,  and
and  satisfy
satisfy  , and
, and  is a local minimizer of
is a local minimizer of  where
where  is the energy functional of problem (1.2).
is the energy functional of problem (1.2).
Theorem 1.4.
Assume  hold and
hold and  satisfies assumption
satisfies assumption  below.
below.
(a3)there exist positive constants  and
and  such that
such that

Then problem (1.2) has a nodal solution in  in addition to two positive solutions
in addition to two positive solutions  and
and  .
.
Among the other interesting problems which are similar to problem (1.2), Bahri and Berestycki [8] and Struwe [9] have investigated the following equation:

where  ,
,  , and
, and  is a bounded domain in
is a bounded domain in  . They found that (1.10) possesses infinitely many solutions. More recently, Tarantello [5] proved that if
. They found that (1.10) possesses infinitely many solutions. More recently, Tarantello [5] proved that if  is the critical Sobolev exponent and
is the critical Sobolev exponent and  satisfying suitable conditions, then (1.10) admits two solutions. For the case when
satisfying suitable conditions, then (1.10) admits two solutions. For the case when  is an unbounded domain, Cao and Zhou [10], Cîrstea and Rădulescu [11], and Ghergu and Rădulescu [12] have been investigated the analogue equation (1.10) involving a subcritical exponent in
is an unbounded domain, Cao and Zhou [10], Cîrstea and Rădulescu [11], and Ghergu and Rădulescu [12] have been investigated the analogue equation (1.10) involving a subcritical exponent in  . Furthermore, Rădulescu and Smets [13] proved existence results for nonautonomous perturbations of critical singular elliptic boundary value problems on infinite cones.
. Furthermore, Rădulescu and Smets [13] proved existence results for nonautonomous perturbations of critical singular elliptic boundary value problems on infinite cones.
This paper is organized as follows. In Section 2, we give some notations and preliminary results. In Section 3, we will prove Theorem 1.1. In Section 4, we establish the existence of nodal solutions.
2. Preliminaries
In this paper, we always assume that  is an unbounded cylinder domain or
is an unbounded cylinder domain or  . Let
. Let  for
for  , and let
, and let  be the first positive eigenfunction of the Dirichlet problem
be the first positive eigenfunction of the Dirichlet problem  in
in  with eigenvalue
with eigenvalue  unless otherwise specified. We denote by
unless otherwise specified. We denote by  and
and  (
( ) universal constants, maybe the constants here should be allowed to depend on
) universal constants, maybe the constants here should be allowed to depend on  and
and  , unless some statement is given. Now we begin our discussion by giving some definitions and some known results.
, unless some statement is given. Now we begin our discussion by giving some definitions and some known results.
We define

Let  be the Sobolev space of the completion of
be the Sobolev space of the completion of  under the norm
under the norm  with the dual space
with the dual space  ,
,  and denote
and denote  the usual scalar product in
the usual scalar product in  . The energy functional of problem (1.2) is given by
. The energy functional of problem (1.2) is given by

here and from now on, we omit " " and "
" and " " in all the integration if there is no other indication. It is well known that
" in all the integration if there is no other indication. It is well known that  is of
is of  in
in  and the solutions of problem (1.2) are the critical points of the energy functional
and the solutions of problem (1.2) are the critical points of the energy functional  (see Rabinowitz [14]).
(see Rabinowitz [14]).
As the energy functional  is not bounded on
is not bounded on  , it is useful to consider the functional on the Nehari manifold
, it is useful to consider the functional on the Nehari manifold

Thus,  if and only if
if and only if

Easy computation shows that  is bounded from below in the set
is bounded from below in the set  . Note that
. Note that  contains every nonzero solution of (1.2).
contains every nonzero solution of (1.2).
Similarly to the method used in Tarantello [5], we split  into three parts:
into three parts:

Let us introduce the problem at infinity associated with problem (1.2) as

We state here some known results for problem (2.6). First of all, we recall that by Esteban [15] and Lien et al. [16], problem (2.6) has a ground state solution  such that
such that

where  ,
,  and
and

Furthermore, from Hsu [2] we can deduce that for any  there exist positive constants
there exist positive constants  such that, for all
such that, for all  ,
,

We also quote the following lemma (see Hsu [17] or K. -J. Chen et al. [18] for the proof) about the decay of positive solution of problem (1.2) which we will use later.
Lemma 2.1.
Assume  and
and  hold. If
hold. If  is a positive solution of problem (1.2), then
is a positive solution of problem (1.2), then
(i) for all
for all  ;
;
(ii) as
as  uniformly for
uniformly for  and
and  for any
for any  ;
;
(iii)for any  there exist positive constants
there exist positive constants  such that, for all
such that, for all  ,
,

We end this preliminaries by the following definition.
Definition 2.2.
Let  ,
,  be a Banach space and
be a Banach space and  .
.
(i) is a
is a  -sequence in
-sequence in  for
for  if
if  and
and  strongly in
strongly in  as
as 
-
(ii)
We say that
 satisfies the
satisfies the  condition if any
condition if any 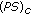 -sequence
-sequence 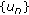 in
in  for
for 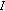 has a convergent subsequence.
has a convergent subsequence.
3. Proof of Theorem 1.1
In this section, we will establish the existence of two positive solutions of problem (1.2).
First, we quote some lemmas for later use (see the proof of Tarantello [5] or Chen [4, Lemmas 2.2, 2.3, and 2.4]).
Lemma 3.1.
Assume  and
and  hold, then for every
hold, then for every  , there exists a unique
, there exists a unique  such that
such that  . In particular, we have
. In particular, we have

and  . Moreover, if
. Moreover, if  , then there exists a unique
, then there exists a unique  such that
such that  . In particular,
. In particular,

 and
and  .
.
Lemma 3.2.
Assume  and
and  hold, then for every
hold, then for every  , we have
, we have

Lemma 3.3.
Assume  and
and  hold, then for every
hold, then for every  , there exist a
, there exist a  and a
and a  -map
-map  satisfying that
satisfying that

Apply Lemmas 3.1, 3.2, 3.3, and Ekeland variational principle [7], and we can establish the existence of the first positive solution.
Proposition 3.4.
Assume  and
and  hold, then the minimization problem
hold, then the minimization problem  is achieved at a point
is achieved at a point  which is a critical point for
which is a critical point for  . Moreover, if
. Moreover, if  and
and  , then
, then  is a positive solution of problem (1.2) and
is a positive solution of problem (1.2) and  is a local minimizer of
is a local minimizer of  .
.
Proof.
Modifying the proof of Chen [4, Proposition 2.5]. Here we omit it.
Since  and
and  , thus, in the search of our second positive solution, it is natural to consider the second minimization problem:
, thus, in the search of our second positive solution, it is natural to consider the second minimization problem:

We will establish the existence of the second positive solution of problem (1.2) by proving that  satisfies the
satisfies the  -condition.
-condition.
Proposition 3.5.
Assume  and
and  hold, then
hold, then  satisfies the
satisfies the  -condition with
-condition with  .
.
Proof.
Let  be a
be a  -sequence for
-sequence for  with
with  . It is easy to see that
. It is easy to see that  is bounded in
is bounded in  , so we can find a
, so we can find a  such that
such that  weakly in
weakly in  up to a subsequence and
up to a subsequence and  is a critical point of
is a critical point of  . Furthermore, we may assume
. Furthermore, we may assume  a.e. in
a.e. in  ,
,  strongly in
strongly in  for all
for all  . Hence we have that
. Hence we have that  and
and

Set  . Then by (3.6) and Brézis and Lieb lemma (see [19]), we obtain
. Then by (3.6) and Brézis and Lieb lemma (see [19]), we obtain

Moreover, by Vitali's lemma and  ,
,

In view of assumptions  and (3.7), (3.8),
and (3.7), (3.8),  and by Lemma 3.2, we obtain
and by Lemma 3.2, we obtain


Hence, we may assume that

By the definition of  , we have
, we have  , combining with (3.11) and
, combining with (3.11) and  , and we get that
, and we get that  . Either
. Either  or
or  . If
. If  , the proof is complete. Assume that
, the proof is complete. Assume that  , from (2.7), (3.9), and (3.11), we get
, from (2.7), (3.9), and (3.11), we get

which is a contradiction. Therefore,  and we conclude that
and we conclude that  strongly in
strongly in  .
.
Let  , let
, let  , and let
, and let  be a constant, we denote
be a constant, we denote  and
and  for
for  where
where  is the ground state solution of problem (2.6) and
is the ground state solution of problem (2.6) and  is the first positive solution of problem (1.2).
is the first positive solution of problem (1.2).
Proposition 3.6.
Assume  and
and  hold, then there exists
hold, then there exists  such that
such that

The following estimates are important to find a path which lies below the first level of the break down of the  condition. Here we use an interaction phenomenon between
condition. Here we use an interaction phenomenon between  and
and  .
.
To give a proof of Proposition 3.6, we need to establish some lemmas.
Lemma 3.7.
Let  , and
, and  is a domain in
is a domain in  . Then for any
. Then for any  , there exists a positive constant
, there exists a positive constant  such that
such that

Proof.
From (2.10), we have for  ,
,

Lemma 3.8.
Let  be a domain in
be a domain in  , and let
, and let  be a vector in
be a vector in  . If
. If  satisfies
satisfies

then

or

Proof.
We know  then
then

Since  as
as  the lemma follows from the Lebesgue's dominated convergence theorem.
the lemma follows from the Lebesgue's dominated convergence theorem.
Now, we give the proof of Proposition 3.6.
The Proof of Proposition 3.6
Recall  , where
, where  is a domain in
is a domain in  . For
. For  , let
, let

We also remark that for all 

and for any  and
and  there exists
there exists  such that for all
such that for all 

Since  is continuous in
is continuous in  , there exists
, there exists  such that for all
such that for all 

and by the fact that  as
as  uniformly in
uniformly in  , then there exists
, then there exists  such that
such that

Thus, we only need to show that there exists a constant  such that
such that

Straightforward computation gives us

where

Thus, we only need to prove that there exists a constant  such that
such that

Now we estimate  and
and  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  . Thus, we can choose
. Thus, we can choose  small enough such that
small enough such that

By (3.21),

Let  ,
, 
 and by applying (3.22), we obtain
and by applying (3.22), we obtain

Let  . Then applying (3.14), we have for
. Then applying (3.14), we have for 

Next from  , (2.9), (3.29), and Lemma 3.8, there exists a
, (2.9), (3.29), and Lemma 3.8, there exists a  such that for any
such that for any  ,
,

From (3.29), we have for  ,
,

Finally, we can choose  large enough such that
large enough such that

Thus from (3.26) and (3.32)–(3.35), we obtain (3.13). This completes the proof of Proposition 3.6.
Proposition 3.9.
For  , there exists a
, there exists a  -sequence
-sequence  for
for  . In particular, we have
. In particular, we have  .
.
Proof.
Set  and define the map
and define the map  given by
given by  . Since the continuity of
. Since the continuity of  follows immediately from its uniqueness and extremal property, thus
follows immediately from its uniqueness and extremal property, thus  is continuous with continuous inverse given by
is continuous with continuous inverse given by  . Clearly
. Clearly  disconnecting
disconnecting  is exactly two components:
is exactly two components:

and  .
.
We will prove that there exists  such that
such that  . Denote
. Denote  . Since
. Since  , we have
, we have

Thus

Therefore, there exists  such that
such that  for
for  . Since
. Since  , then
, then

hence  .
.
 disconnects
disconnects  in exactly two components, so we can find an
in exactly two components, so we can find an  such that
such that  . Therefore
. Therefore  , which follows from Proposition 3.6.
, which follows from Proposition 3.6.
Analogously to the proof of Proposition 3.4, by the Ekeland variational principle we can show that there exists a  -sequence
-sequence  for
for  .
.
Proposition 3.10.
Assume  and
and  hold, then the functional
hold, then the functional  has a minimizer
has a minimizer  which is also a critical point of
which is also a critical point of  and
and  for
for  .
.
Proof.
From Propsitions 3.5 and 3.9, we can deduce that  strongly in
strongly in  . Consequently,
. Consequently,  is a critical point of
is a critical point of  ,
,  (since
(since  is closed) and
is closed) and  .
.
By Lemma 3.1, we can choose a number  such that
such that  . Since
. Since  . Applying Lemma 3.1 again, we conclude that
. Applying Lemma 3.1 again, we conclude that

Hence  . So we can always take
. So we can always take  . By the maximum principle for weak solutions (see Gilbarg and Trudinger [20]) we can show that if
. By the maximum principle for weak solutions (see Gilbarg and Trudinger [20]) we can show that if  , then
, then  in
in  .
.
The proof of Theorem 1.1
By Propositions 3.4 and 3.10, we obtain the conclusion of Theorem 1.1.
4. Existence of Nodal Solution
In this section, we will study the existence of nodal solutions for problem (1.2). To this end, we need to compare some different minimization problems. Define

Here, we use notation  . Set
. Set


Then we have
Proposition 4.1.
-
(a)
If
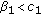 , then the minimization problem (4.2) attains its infimum at a point which defines a sign changing critical point of
, then the minimization problem (4.2) attains its infimum at a point which defines a sign changing critical point of  .
. -
(b)
Analogously, if
 the same conclusion holds for the minimization problem (4.3).
the same conclusion holds for the minimization problem (4.3).
Proof.
The proof is almost the same as that in Tarantello [6, Proposition 3.1] .
The above proposition would yield the conclusion for the main theorem only if the given relations between  , and
, and  could be established. While it is not clear whether or not such inequalities should hold, we will use these values to compare with another minimization problem. Namely, set
could be established. While it is not clear whether or not such inequalities should hold, we will use these values to compare with another minimization problem. Namely, set

and define

It is clear that  . Since
. Since  satisfies
satisfies  condition only locally, we need the following upper bound for
condition only locally, we need the following upper bound for  . Recall that
. Recall that  ,
,  and
and  where
where  and
and  is the ground state solution of problem (2.6).
is the ground state solution of problem (2.6).
Lemma 4.2.
Assume  ,
,  and
and  hold. For any fixed
hold. For any fixed  , there exist
, there exist  such that
such that

and for  large,
large,

Proof.
To prove (4.6), it suffices to show that there exist  and
and  such that
such that

To this purpose, let

For  , denote by
, denote by  and
and  the positive values given by Lemma 3.1 according to which we have
the positive values given by Lemma 3.1 according to which we have

Note that  and
and  are continuous with respect to
are continuous with respect to  satifying
satifying

Therefore, by the continuity of  , we can find
, we can find  such that
such that  . This gives (4.8) with
. This gives (4.8) with  and
and  .
.
To prove (4.7), we only need to estimate  for
for  and
and  . First, it is obvious that the structure of
. First, it is obvious that the structure of  guarantees the existence of
guarantees the existence of  (independent of
(independent of  large) such that
large) such that  , for all
, for all  . On the other hand, for
. On the other hand, for  , since
, since  is continuous in
is continuous in  , there exists
, there exists  small enough such that
small enough such that

At this point, we find large  , such that
, such that  holds for all
holds for all  and
and  :
:

By (4.13) and the following elementary inequality:

where  is some positive constant, we have
is some positive constant, we have

Without loss of generality, we may assume  , and
, and  where
where  ,
,  and
and  are given in
are given in  and
and  , respectively.
, respectively.
(i)First, by the Hölder inequality and (2.9),

From (2.9), (2.10), and applying Lemma 3.8, there exists a  such that for
such that for 

Similarly, we also obtain

and there exists a  such that for
such that for 

(ii)Since  satisfies assumption
satisfies assumption  and by Lemma 3.8, there exists a
and by Lemma 3.8, there exists a  such that for
such that for  ,
,

By  , (2.9), and Lemma 3.8, there exists a
, (2.9), and Lemma 3.8, there exists a  such that for
such that for  ,
,

(iii)Note that the constants  (
( ) in (i), (ii) are independent of
) in (i), (ii) are independent of  . Thus, by (i), (ii),
. Thus, by (i), (ii),  and let
and let  , we can find a
, we can find a  such that for
such that for  ,
,

Combining (4.15) and (4.22), we obtain that there exists a  such that for
such that for  ,
,

This completes the proof of Lemma 4.2.
Proposition 4.3.
Assume  and
and  hold. If
hold. If  and
and  , then the minimization problem
, then the minimization problem  attains its infimum at
attains its infimum at  which defines a changing sign critical point of
which defines a changing sign critical point of  .
.
Proof.
It is obvious that  is closed. Exactly as in the proof of [6, Proposition 3.2], by means of Ekeland's principle, we derive a
is closed. Exactly as in the proof of [6, Proposition 3.2], by means of Ekeland's principle, we derive a  -sequence
-sequence  for
for  . In particular, we have
. In particular, we have  , for some constants
, for some constants  and
and  . Thus, we can take a subsequence, also denoted by
. Thus, we can take a subsequence, also denoted by  , such that
, such that  weakly in
weakly in  . We start by showing that
. We start by showing that  .
.
Indeed, if by contradiction we assume, for instant, that  , then we can deduce that
, then we can deduce that

On the other hand,

By (4.24) and  , we may assume that
, we may assume that

Using the argument in the proof of Proposition 3.5, by (2.7), (4.24), and (4.25), we can deduce that  and
and

However, by Lemma 4.2,  ; that is,
; that is,  which contradicts (4.27). A similar argument applies to
which contradicts (4.27). A similar argument applies to  . Therefore,
. Therefore,  is a weak solution of problem (1.2) changing sign and
is a weak solution of problem (1.2) changing sign and  .
.
Set  and
and  with
with  weakly in
weakly in  . Note that
. Note that

In view of Proposition 3.9 and Lemma 4.2, we also have

Therefore, we must have

Without loss of generality, we suppose

By (4.24), we have

We claim that  . Indeed, we assume
. Indeed, we assume  is bounded below, as above, (4.28) and (4.32) imply
is bounded below, as above, (4.28) and (4.32) imply  , contradicting (4.31). In the same way, if
, contradicting (4.31). In the same way, if  , we can also prove
, we can also prove  . Hence we have
. Hence we have  or
or  ; that is,
; that is,  or
or  . By assumptions
. By assumptions  and
and  , we conclude that
, we conclude that  .
.
If we write  with
with  weakly in
weakly in  , we have
, we have

Furthermore, by Lemma 4.2, we have

We claim that  . Indeed, we assume
. Indeed, we assume  is bounded below, as above, (4.33) imply
is bounded below, as above, (4.33) imply  , contradicting (4.34). Consequently,
, contradicting (4.34). Consequently,  strongly in
strongly in  and
and  .
.
The Proof of Theorems 1.2–1.4
The conclusion of Theorem 1.2 follows immediately from Theorem 1.2 and Propositions 4.1 and 4.3. With the same argument, we also have that Theorems 1.3 and 1.4 hold for  .
.
References
Zhu XP: Multiple entire solutions of a semilinear elliptic equation. Nonlinear Analysis: Theory, Methods & Applications 1988, 12(11):1297–1316. 10.1016/0362-546X(88)90061-2
Hsu T-S: Multiple solutions for semilinear elliptic equations in unbounded cylinder domains. Proceedings of the Royal Society of Edinburgh. Section A 2004, 134(4):719–731. 10.1017/S0308210500003449
Adachi S, Tanaka K: Four positive solutions for the semilinear elliptic equation: in . Calculus of Variations and Partial Differential Equations 2000, 11(1):63–95. 10.1007/s005260050003
Chen K-J: Multiplicity of positive and nodal solutions for an inhomogeneous nonlinear elliptic problem. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(1):194–210. 10.1016/j.na.2007.11.046
Tarantello G: On nonhomogeneous elliptic equations involving critical Sobolev exponent. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1992, 9(3):281–304.
Tarantello G: Multiplicity results for an inhomogeneous Neumann problem with critical exponent. Manuscripta Mathematica 1993, 81(1–2):57–78.
Ekeland I: On the variational principle. Journal of Mathematical Analysis and Applications 1974, 47: 324–353. 10.1016/0022-247X(74)90025-0
Bahri A, Berestycki H: A perturbation method in critical point theory and applications. Transactions of the American Mathematical Society 1981, 267(1):1–32. 10.1090/S0002-9947-1981-0621969-9
Struwe M: Infinitely many critical points for functionals which are not even and applications to superlinear boundary value problems. Manuscripta Mathematica 1980, 32(3–4):335–364. 10.1007/BF01299609
Cao D-M, Zhou H-S: Multiple positive solutions of nonhomogeneous semilinear elliptic equations in . Proceedings of the Royal Society of Edinburgh. Section A 1996, 126(2):443–463. 10.1017/S0308210500022836
Cîrstea F, Rădulescu V: Multiple solutions of degenerate perturbed elliptic problems involving a subcritical Sobolev exponent. Topological Methods in Nonlinear Analysis 2000, 15(2):283–300.
Ghergu M, Rădulescu V: Singular elliptic problems with lack of compactness. Annali di Matematica Pura ed Applicata 2006, 185(1):63–79. 10.1007/s10231-004-0128-2
Rădulescu V, Smets D: Critical singular problems on infinite cones. Nonlinear Analysis: Theory, Methods & Applications 2003, 54(6):1153–1164. 10.1016/S0362-546X(03)00131-7
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. American Mathematical Society, Washington, DC, USA; 1986:viii+100.
Esteban MJ: Nonlinear elliptic problems in strip-like domains: symmetry of positive vortex rings. Nonlinear Analysis: Theory, Methods & Applications 1983, 7(4):365–379. 10.1016/0362-546X(83)90090-1
Lien WC, Tzeng SY, Wang HC: Existence of solutions of semilinear elliptic problems on unbounded domains. Differential and Integral Equations 1993, 6(6):1281–1298.
Hsu T-S: Existence of multiple positive solutions of subcritical semilinear elliptic problems in exterior strip domains. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(6):1203–1228. 10.1016/j.na.2005.05.062
Chen K-J, Chen K-C, Wang H-C: Symmetry of positive solutions of semilinear elliptic equations in infinite strip domains. Journal of Differential Equations 1998, 148(1):1–8. 10.1006/jdeq.1998.3463
Brézis H, Lieb E: A relation between pointwise convergence of functions and convergence of functionals. Proceedings of the American Mathematical Society 1983, 88(3):486–490.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Grundlehren der Mathematischen Wissenschaften. Volume 224. 2nd edition. Springer, Berlin, Germany; 1983:xiii+513.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hsu, TS. Multiplicity of Positive and Nodal Solutions for Nonhomogeneous Elliptic Problems in Unbounded Cylinder Domains. Bound Value Probl 2009, 687385 (2009). https://doi.org/10.1155/2009/687385
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/687385
 satisfies the
satisfies the  condition if any
condition if any 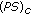 -sequence
-sequence 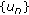 in
in  for
for 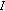 has a convergent subsequence.
has a convergent subsequence.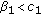 , then the minimization problem (4.2) attains its infimum at a point which defines a sign changing critical point of
, then the minimization problem (4.2) attains its infimum at a point which defines a sign changing critical point of  .
. the same conclusion holds for the minimization problem (4.3).
the same conclusion holds for the minimization problem (4.3).