- Research Article
- Open access
- Published:
On Some Generalizations Bellman-Bihari Result for Integro-Functional Inequalities for Discontinuous Functions and Their Applications
Boundary Value Problems volume 2009, Article number: 808124 (2009)
Abstract
We present some new nonlinear integral inequalities Bellman-Bihari type with delay for discontinuous functions (integro-sum inequalities; impulse integral inequalities). Some applications of the results are included: conditions of boundedness (uniformly), stability by Lyapunov (uniformly), practical stability by Chetaev (uniformly) for the solutions of impulsive differential and integro-differential systems of ordinary differential equations.
1. Introduction
The first generalizations of the Bihari result for discontinuous functions which satisfy nonlinear impulse inequality (integro-sum inequality) are connected with such types of inequalities:
-
(a)
 (11)
(11)
-
(b)
 (12)
(12)
Which are studied in the publications by Bainov, Borysenko, Iovane, Laksmikantham, Leela, Martynyuk, Mitropolskiy, Samoilenko ([1–13]), and in many others. In these investigations the method of integral inequalities for continuous functions is generalized to the case of piecewise continuous (one-dimensional inequalities) and discontinuous (multidimensional inequalities) functions.
For the generalization of the integral inequalities method for discontinuous functions and for their applications to qualitative analysis of impulsive systems: existence, uniqueness, boundedness, comparison, stability, and so forth. We refer to the results [2–5, 12, 14] and for periodic boundary value problems we cite [15–17]. More recently, a novel variational approach appeared in [18]. This approach to impulsive differential equations also used the critical point theory for the existence of solutions of a nonlinear Dirichlet impulsive problem and in [19] some new comparison principles and the monotone iterative technique to establish a more general existence theorem for a periodic boundary value problem. Reference [20] is very interesting in that it gives a complete overview of the state-of-the-art of the impulsive differential, inclusions.
In this paper, in Section 2, we investigate new analogies Bihari results for piecewise continuous functions and, in Section 3, the conditions of boundedness, stability, practical stability of the solutions of nonlinear impulsive differential and integro-differential systems.
2. General Bihari Theorems for Integro-Functional Inequalities for Discontinuous Functions
Let us consider the class  of continuous functions
of continuous functions  (
( is the delaying argument). The following holds.
is the delaying argument). The following holds.
Theorem 2.1.
-
(a)
Let one suppose that for
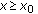 the following integro-sum functional inequality holds:
the following integro-sum functional inequality holds: 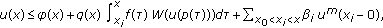 (21)
(21)
where  is a positive nondecreasing function,
is a positive nondecreasing function,  function
function  is a nonnegative piecewise-continuous,with I-st kind of discontinuities in the points
is a nonnegative piecewise-continuous,with I-st kind of discontinuities in the points  ,
,  belongs to the class
belongs to the class  .
.
-
(b)
Function
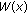 satisfies such conditions:
satisfies such conditions:
(i)
(ii)
(iii) is nondecreasing.
is nondecreasing.
Then for arbitrary  the next estimate holds:
the next estimate holds:




Proof.
It follows from inequality (2.1)

Denoting by

then

Let us consider the interval  Then
Then

where  So it results in
So it results in

and estimate (2.2) is valid in  .
.
Let us suppose that for  estimate (2.2) is fulfilled. Then for every
estimate (2.2) is fulfilled. Then for every we have
we have

where  is determined from (2.3)–(2.5).
is determined from (2.3)–(2.5).
Taking into account such inequality

we obtain estimate (2.2) for every  .
.
Let us consider the class  of functions
of functions  such that
such that
(i) positive, continuous, nondecreasing for
positive, continuous, nondecreasing for ;
;
(ii)
(iii)
The following result is proved.
Theorem 2.2.
Suppose that the part (a) of Theorem 2.1 is valid and function  belongs to the class
belongs to the class  Then for arbitrary
Then for arbitrary  such estimate holds:
such estimate holds:

where

and 
Proof.
By using the previous theorem we have  . On the interval
. On the interval 

Then

Taking into account estimate (2.16), we obtain

Then in  we have
we have

As in the previously theorem, the proof is completed by using the inductive method.
The following result is easily to obtain
Theorem 2.3.
Suppose that for  the next inequality holds:
the next inequality holds:

where functions  are real nonnegative for
are real nonnegative for , function
, function  satisfies conditions (i),…,(iii) of Theorem 2.1.
satisfies conditions (i),…,(iii) of Theorem 2.1.
Then for  it results in
it results in

where

The proof the same procedure as that of (Iovane [21, Theorems 2.1 and 3.1]).
Corollary 2.4.
Suppose that
(a) , then the result of Theorem 2.1 coincides with the result [22, Theorem 3.7.1, page 232];
, then the result of Theorem 2.1 coincides with the result [22, Theorem 3.7.1, page 232];
(b) then the result of Theorem 2.1 coincides with result [12, Proposition 2.3, page 2143];
then the result of Theorem 2.1 coincides with result [12, Proposition 2.3, page 2143];
(c) , then one obtains the analogy of Gronwall- Bellman result for discontinuous functions [23, Lemma 1] and estimate (2.2) reduces in the following form:
, then one obtains the analogy of Gronwall- Bellman result for discontinuous functions [23, Lemma 1] and estimate (2.2) reduces in the following form:

(d) , then one obtains the result [21, Theorem 2.1] and estimate (2.2) are as follows:
, then one obtains the result [21, Theorem 2.1] and estimate (2.2) are as follows:

(e) then one obtains the analogy of Bihari result for discontinuous functions [23, Lemma 2] and estimate (2.2) reduces as follows are reduced:
then one obtains the analogy of Bihari result for discontinuous functions [23, Lemma 2] and estimate (2.2) reduces as follows are reduced:

such that

-
(f)
W(u) = um,, m> 0, then estimate (2.2) reduces as follows (see [21, Theorem 2.2]):
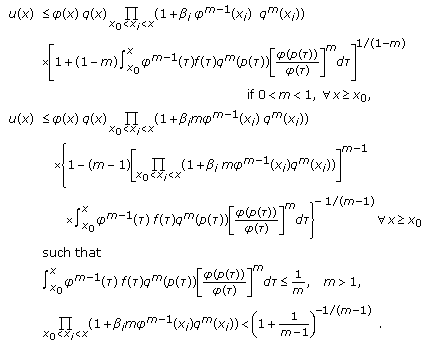 (226)
(226)
(g)Suppose that in Theorem 2.3 then estimates (2.20), (2.21) reduce as shown:
then estimates (2.20), (2.21) reduce as shown:

which coincide with result of [21, Theorem 3.1] for .
.
3. Applications
Let us consider the following system of differential equations

where .
.
Let us assume that  and
and  are defined in the domain
are defined in the domain  and satisfy such conditions:
and satisfy such conditions:
(a)
W satisfies conditions (i)–(iii) of Theorem 2.1;
(b) .
.
Consider  the solution of Cauchy problem for system (3.1). Then
the solution of Cauchy problem for system (3.1). Then

from which it follows

By using the result of Theorem 2.1 and estimate (2.2) we obtain

where

Let us consider some particular cases of  .
.
If  , estimate (3.4) is reduced in such form
, estimate (3.4) is reduced in such form

Then such result holds.
Proposition 3.1.
Let the following conditions be fulfilled for system (3.1) :
(i)
(ii)
(iii)
(iv)
Then one has:
(a)All solutions of system (3.1) are bounded (uniformly, if  are independent of
are independent of  ) and such estimate is valid:
) and such estimate is valid:

(b)The trivial solution of system (3.1) is stable by Lyapunov (uniformly stable relative  , if
, if  ).
).
Remark 3.2.
If conditions I–IV of Proposition 3.1 are valid and  then the trivial solution is
then the trivial solution is  -stable by Chetaev (uniformly
-stable by Chetaev (uniformly  -stable, if
-stable, if  ,
,  is independent of
is independent of  ).
).
If  the estimate (3.4) is reduced in such form
the estimate (3.4) is reduced in such form



From estimate (3.8) the next propositions follow.
Proposition 3.3.
Suppose that such conditions occur:
(a)
(b)estimates ii–iv of Proposition 3.1 be fulfilled.
Then all the solutions of system (3.1) are bounded (uniformly if  ).
).
Remark 3.4.
Suppose that conditions (a), (b) of Proposition 3.3 are valid and

Then trivial solution of system (3.1) is  -stable by Chetaev (uniformly if
-stable by Chetaev (uniformly if  is independent of
is independent of  ).
).
Proposition 3.5.
Let conditions ii–iv of Proposition 3.1 be fulfilled for system (3.1), inequality (3.10) holds and

Then trivial solution of system (3.1) is stable by Lyapunov (uniformly if  ).
).
Remark 3.6.
If  , and
, and  the conditions of boundedness, stability,
the conditions of boundedness, stability,  -stability is investigated in [14, see Theorems 3.4–3.6]; the estimates of the solutions of system (3.1) with non-Lipschitz type of discontinuities are investigated in [23, see Proposition 1, Proposition 2].
-stability is investigated in [14, see Theorems 3.4–3.6]; the estimates of the solutions of system (3.1) with non-Lipschitz type of discontinuities are investigated in [23, see Proposition 1, Proposition 2].
Let us consider the following impulsive system of integro-differential equations:

where and defined in the domain
and defined in the domain  ,
,  .
.
We suppose that such conditions are valid:
(i)
(ii)
(iii) .
.
It is easy to see that


From estimate (3.15) such result follows.
Proposition 3.7.
Let one suppose that for system (3.13) conditions (i)–(iii) take place for  and the following estimates are fulfilled:
and the following estimates are fulfilled:
(a) ;
;
(b)
Then we have:
(i)All solutions of system (3.13) are bounded and satisfy the estimate:

(ii)The trivial solution of system (3.13) is stable by Lyapunov (uniformly, if  ).
).
-
(iii)
The trivial solution of system (3.13) is
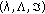 -stable by Chetaev (uniformly if
-stable by Chetaev (uniformly if  is independent of
is independent of 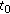 ) and
) and 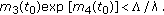
References
Banov D, Simeonov P: Integral Inequalities and Applications, Mathematics and Its Applications. Volume 57. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xii+245.
Borysenko SD, Iovane G, Giordano P: Investigations of the properties motion for essential nonlinear systems perturbed by impulses on some hypersurfaces. Nonlinear Analysis: Theory, Methods & Applications 2005, 62(2):345–363. 10.1016/j.na.2005.03.031
Borysenko SD, Ciarletta M, Iovane G: Integro-sum inequalities and motion stability of systems with impulse perturbations. Nonlinear Analysis: Theory, Methods & Applications 2005, 62(3):417–428. 10.1016/j.na.2005.03.032
Borysenko S, Iovane G: About some new integral inequalities of Wendroff type for discontinuous functions. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(10):2190–2203. 10.1016/j.na.2006.03.008
Hu SC, Lakshmikantham V, Leela S: Impulsive differential systems and the pulse phenomena. Journal of Mathematical Analysis and Applications 1989, 137(2):605–612. 10.1016/0022-247X(89)90266-7
Lakshmikantham V, Leela S: Differential and Integral Inequalities, Theory and Applications. Academic Press, New York, NY, USA; 1969.
Lakshmikantham V, Leela S, Mohan Rao Rama M: Integral and integro-differential inequalities. Applicable Analysis 1987, 24(3):157–164. 10.1080/00036818708839660
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Martyhyuk AA, Lakshmikantham V, Leela S: Stability of Motion: the Method of Integral Inequalities. Naukova Dumka, Kyiv, Russia; 1989.
Mitropolskiy YuA, Leela S, Martynyuk AA: Some trends in V. Lakshmikantham's investigations in the theory of differential equations and their applications. Differentsial'nye Uravneniya 1986, 22(4):555–572.
Mitropolskiy YuA, Samoilenko AM, Perestyuk N: On the problem of substantiation of overoging method for the second equations with impulse effect. Ukrainskii Matematicheskii Zhurnal 1977, 29(6):750–762.
Mitropolskiy YuA, Iovane G, Borysenko SD: About a generalization of Bellman-Bihari type inequalities for discontinuous functions and their applications. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(10):2140–2165. 10.1016/j.na.2006.03.006
Samoilenko AM, Perestyuk N: Differential Equations with Impulse Effect. Visha Shkola, Kyiv, Russia; 1987.
Gallo A, Piccirillo AM: About new analogies of Gronwall-Bellman-Bihari type inequalities for discontinuous functions and estimated solutions for impulsive differential systems. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(5):1550–1559. 10.1016/j.na.2006.07.038
Nieto JJ: Impulsive resonance periodic problems of first order. Applied Mathematics Letters 2002, 15(4):489–493. 10.1016/S0893-9659(01)00163-X
Nieto JJ: Basic theory for nonresonance impulsive periodic problems of first order. Journal of Mathematical Analysis and Applications 1997, 205(2):423–433. 10.1006/jmaa.1997.5207
Nieto JJ: Periodic boundary value problems for first-order impulsive ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2002, 51(7):1223–1232. 10.1016/S0362-546X(01)00889-6
Luo Z, Nieto JJ: New results for the periodic boundary value problem for impulsive integro-differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(6):2248–2260. 10.1016/j.na.2008.03.004
Nieto JJ, O'Regan D: Variational approach to impulsive differential equations. Nonlinear Analysis: Real World Applications 2009, 10(2):680–690. 10.1016/j.nonrwa.2007.10.022
Benchohra M, Henderson J, Ntouyas S: Impulsive Differential Equations and Inclusions, Contemporary Mathematics and Its Applications. Volume 2. Hindawi Publishing Corporation, New York, NY, USA; 2006:xiv+366.
Iovane G: Some new integral inequalities of Bellman-Bihari type with delay for discontinuous functions. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(2):498–508. 10.1016/j.na.2005.11.043
Samoilenko A, Borysenko S, Cattani C, Matarazzo G, Yasinsky V: Differential Models: Stability, Inequalities and Estimates. Naukova Dumka, Kiev, Russia; 2001:328.
Borysenko DS, Gallo A, Toscano R: Integral inequalities Gronwall-Bellman type for discontinuous functions and estimates of solutions impulsive systems. Proc.DE@CAS, 2005, Brest 5–9.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gallo, A., Piccirillo, A.M. On Some Generalizations Bellman-Bihari Result for Integro-Functional Inequalities for Discontinuous Functions and Their Applications. Bound Value Probl 2009, 808124 (2009). https://doi.org/10.1155/2009/808124
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/808124


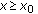 the following integro-sum functional inequality holds:
the following integro-sum functional inequality holds: 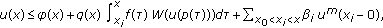
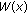 satisfies such conditions:
satisfies such conditions: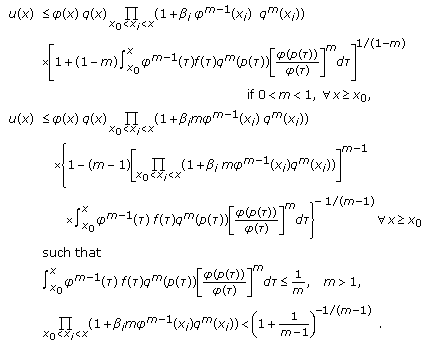
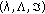 -stable by Chetaev (uniformly if
-stable by Chetaev (uniformly if  is independent of
is independent of 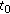 ) and
) and