- Research Article
- Open access
- Published:
A Note on Generalized Fractional Integral Operators on Generalized Morrey Spaces
Boundary Value Problems volume 2009, Article number: 835865 (2010)
Abstract
We show some inequalities for generalized fractional integral operators on generalized Morrey spaces. We also show the boundedness property of the generalized fractional integral operators on the predual of the generalized Morrey spaces.
1. Introduction
The present paper is an offspring of [1]. We obtain some inequalities for generalized fractional integral operators on generalized Morrey spaces. We also show the boundedness property of the generalized fractional integral operators on the predual of the generalized Morrey spaces. They generalize what was shown in [1]. We will go through the same argument as [1].
For  the classical fractional integral operator
the classical fractional integral operator  and the classical fractional maximal operator
and the classical fractional maximal operator  are given by
are given by

In the present paper, we generalize the parameter  . Let
. Let  be a suitable function. We define the generalized fractional integral operator
be a suitable function. We define the generalized fractional integral operator  and the generalized fractional maximal operator
and the generalized fractional maximal operator  by
by

Here, we use the notation  to denote the family of all cubes in
to denote the family of all cubes in  with sides parallel to the coordinate axes,
with sides parallel to the coordinate axes,  , to denote the sidelength of
, to denote the sidelength of  and
and  to denote the volume of
to denote the volume of  . If
. If  ,
,  , then we have
, then we have  and
and  .
.
A well-known fact in partial differential equations is that  is an inverse of
is an inverse of  . The operator
. The operator  admits an expression of the form
admits an expression of the form  for some
for some  . For more details of this operator we refer to [2]. As we will see, these operators will fall under the scope of our main results.
. For more details of this operator we refer to [2]. As we will see, these operators will fall under the scope of our main results.
Among other function spaces, it seems that the Morrey spaces reflect the boundedness properties of the fractional integral operators. To describe the Morrey spaces we recall some definitions and notation. All cubes are assumed to have their sides parallel to the coordinate axes. For  we use
we use  to denote the cube with the same center as
to denote the cube with the same center as  , but with sidelength of
, but with sidelength of  .
.  denotes the Lebesgue measure of
denotes the Lebesgue measure of  .
.
Let  and
and  be a suitable function. For a function
be a suitable function. For a function  locally in
locally in  we set
we set

We will call the Morrey space  the subset of all functions
the subset of all functions  locally in
locally in  for which
for which  is finite. Applying Hölder's inequality to (1.3), we see that
is finite. Applying Hölder's inequality to (1.3), we see that  provided that
provided that  . This tells us that
. This tells us that  when
when  . We remark that without the loss of generality we may assume
. We remark that without the loss of generality we may assume

(See [1].) Hereafter, we always postulate (1.4) on  .
.
If  ,
,  ,
,  coincides with the usual Morrey space and we write this for
coincides with the usual Morrey space and we write this for  and the norm for
and the norm for  . Then we have the inclusion
. Then we have the inclusion

when  .
.
In the present paper, we take up some relations between the generalized fractional integral operator  and the generalized fractional maximal operator
and the generalized fractional maximal operator  in the framework of the Morrey spaces
in the framework of the Morrey spaces  (Theorem 1.2). In the last section, we prove a dual version of Olsen's inequality on predual of Morrey spaces (Theorem 3.1). As a corollary (Corollary 3.2), we have the boundedness properties of the operator
(Theorem 1.2). In the last section, we prove a dual version of Olsen's inequality on predual of Morrey spaces (Theorem 3.1). As a corollary (Corollary 3.2), we have the boundedness properties of the operator  on predual of Morrey spaces.
on predual of Morrey spaces.
Let  be a function. By the Dini condition we mean that
be a function. By the Dini condition we mean that  fulfills
fulfills

while the doubling condition on  (with a doubling constant
(with a doubling constant  ) is that
) is that  satisfies
satisfies

We notice that (1.4) is stronger than the doubling condition. More quantitatively, if we assume (1.4), then  satisfies the doubling condition with the doubling constant
satisfies the doubling condition with the doubling constant  . A simple consequence that can be deduced from the doubling condition of
. A simple consequence that can be deduced from the doubling condition of  is that
is that

The key observation made in [1] is that it is frequently convenient to replace  satisfying (1.6) and (1.7) by
satisfying (1.6) and (1.7) by  :
:

Before we formulate our main results, we recall a typical result obtained in [1].
Proposition 1.1 (see [1, Theorem 1.3]).
Let

 and
and  . Suppose that
. Suppose that  is nonincreasing. Then
is nonincreasing. Then

where the constant  is independent of
is independent of  and
and  .
.
The aim of the present paper is to generalize the function spaces to which  and
and  belong. With theorem 1.2, which we will present just below, we can replace
belong. With theorem 1.2, which we will present just below, we can replace  with
with  and
and  with
with  . We now formulate our main theorems. In the sequel we always assume that
. We now formulate our main theorems. In the sequel we always assume that  satisfies (1.6) and (1.7), and
satisfies (1.6) and (1.7), and  is used to denote various positive constants.
is used to denote various positive constants.
Theorem 1.2.
Let

Suppose that  and
and  are nondecreasing but that
are nondecreasing but that  and
and  are nonincreasing. Assume also that
are nonincreasing. Assume also that

then

where the constant  is independent of
is independent of  and
and  .
.
Remark 1.3.
Let  and
and  . Then
. Then  and
and  satisfy the assumption (1.13). Indeed,
satisfy the assumption (1.13). Indeed,

Hence, Theorem 1.2 generalizes Proposition 1.1.
Letting  and
and  in Theorem 1.2, we obtain the result of how
in Theorem 1.2, we obtain the result of how  controls
controls  .
.
Corollary 1.4.
Let  . Suppose that
. Suppose that

then

Corollary 1.4 generalizes [3, Theorem 4.2]. Letting  in Theorem 1.2, we also obtain the condition on
in Theorem 1.2, we also obtain the condition on  and
and  under which the mapping
under which the mapping

is bounded.
Corollary 1.5.
Let

Suppose that

then

In particular, if  , then
, then

Here,  denotes the Hardy-Littlewood maximal operator defined by
denotes the Hardy-Littlewood maximal operator defined by

We will establish that  is bounded on
is bounded on  when
when  (Lemma 2.2). Therefore, the second assertion is immediate from the first one.
(Lemma 2.2). Therefore, the second assertion is immediate from the first one.
Theorem 1.6.
Let  . Suppose that
. Suppose that  and
and  are nondecreasing but that
are nondecreasing but that  and
and  are nonincreasing. Suppose also that
are nonincreasing. Suppose also that

then

where the constant  is independent of
is independent of  and
and  .
.
Theorem 1.6 extends [4, Theorem 2], [1, Theorem 1.1], and [5, Theorem 1]. As the special case  and
and  in Theorem 1.6 shows, this theorem covers [1, Remark 2.8].
in Theorem 1.6 shows, this theorem covers [1, Remark 2.8].
Corollary 1.7 (see [1, Remark 2.8], see also [6–8]).
Let  . Suppose that
. Suppose that

then

Nakai generalized Corollary 1.7 to the Orlicz-Morrey spaces ([9, Theorem 2.2] and [10, Theorem 7.1]).
We dare restate Theorem 1.6 in the special case when  is the fractional integral operator
is the fractional integral operator  . The result holds by letting
. The result holds by letting  ,
,  and
and  .
.
Proposition 1.8 (see [1, Proposition 1.7]).
Let  ,
,  ,
,  , and
, and  . Suppose that
. Suppose that  ,
,  ,
,  ,
,  , and
, and  then
then

where the constant  is independent of
is independent of  and
and  .
.
Proposition 1.8 extends [4, Theorem 2] (see [1, Remark 1.9]).
Remark 1.9.
The special case  and
and  in Proposition 1.8 corresponds to the classical theorem due to Adams (see [11]).
in Proposition 1.8 corresponds to the classical theorem due to Adams (see [11]).
The fractional integral operator  ,
,  , is bounded from
, is bounded from  to
to  if and only if the parameters
if and only if the parameters  and
and  satisfy
satisfy  and
and  .
.
Using naively the Adams theorem and Hölder's inequality, one can prove a minor part of  in Proposition 1.8. That is, the proof of Proposition 1.8 is fundamental provided
in Proposition 1.8. That is, the proof of Proposition 1.8 is fundamental provided  Indeed, by virtue of the Adams theorem we have, for any cube
Indeed, by virtue of the Adams theorem we have, for any cube  ,
,

The condition  ,
,  reads
reads

These yield

if  . In view of inclusion (1.5), the same can be said when
. In view of inclusion (1.5), the same can be said when  . Also observe that
. Also observe that  Hence we have
Hence we have  . Thus, since the condition
. Thus, since the condition  , Proposition 1.8 is significant only when
, Proposition 1.8 is significant only when  The case
The case  (the case of the Lebesgue spaces) corresponds (so-called) to the Fefferan-Phong inequality (see [12]). An inequality of the form
(the case of the Lebesgue spaces) corresponds (so-called) to the Fefferan-Phong inequality (see [12]). An inequality of the form

is called the trace inequality and is useful in the analysis of the Schrödinger operators. For example, Kerman and Sawyer utilized an inequality of type (1.32) to obtain an eigenvalue estimates of the operators (see [13]). By letting  , we obtain a sharp estimate on the constant
, we obtain a sharp estimate on the constant  in (1.32).
in (1.32).
In [14], we characterized the range of  , which motivates us to consider Proposition 1.8.
, which motivates us to consider Proposition 1.8.
Proposition 1.10 (see [14]).
Let  ,
,  , and
, and  . Assume that
. Assume that

(1) is continuous but not surjective.
is continuous but not surjective.
(2)Let  be an auxiliary function chosen so that
be an auxiliary function chosen so that  ,
,  and that
and that  ,
,  ,
,  . Then the norm equivalence
. Then the norm equivalence

holds for  , where
, where  denotes the Fourier transform.
denotes the Fourier transform.
In view of this proposition  is not a good space to describe the boundedness of
is not a good space to describe the boundedness of  , although we have (1.29). As we have seen by using Hölder's inequality in Remark 1.9, if we use the space
, although we have (1.29). As we have seen by using Hölder's inequality in Remark 1.9, if we use the space  , then we will obtain a result weaker than Proposition 1.8.
, then we will obtain a result weaker than Proposition 1.8.
Finally it would be interesting to compare Theorem 1.2 with the following Theorem 1.11.
Theorem 1.11.
Let  . Suppose that
. Suppose that  ,
,  , and
, and  are nondecreasing and that
are nondecreasing and that  and
and  are nonincreasing. Then
are nonincreasing. Then

where the constant  is independent of
is independent of  and
and  .
.
Theorem 1.11 generalizes [1, Theorem 1.7] and the proof remains unchanged except some minor modifications caused by our generalization of the function spaces to which  and
and  belong. So, we omit the proof in the present paper.
belong. So, we omit the proof in the present paper.
2. Proof of Theorems
For any  we will write
we will write  for the conjugate number defined by
for the conjugate number defined by  . Hereafter, for the sake of simplicity, for any
. Hereafter, for the sake of simplicity, for any  and
and  we will write
we will write

2.1. Proof of Theorem 1.2
First, we will prove Theorem 1.2. Except for some sufficient modifications, the proof of the theorem follows the argument in [15]. We denote by  the family of all dyadic cubes in
the family of all dyadic cubes in  . We assume that
. We assume that  and
and  are nonnegative, which may be done without any loss of generality thanks to the positivity of the integral kernel. We will denote by
are nonnegative, which may be done without any loss of generality thanks to the positivity of the integral kernel. We will denote by  the ball centered at
the ball centered at  and of radius
and of radius  . We begin by discretizing the operator
. We begin by discretizing the operator  following the idea of Pérez (see [16]):
following the idea of Pérez (see [16]):

where we have used the doubling condition of  for the first inequality. To prove Theorem 1.2, thanks to the doubling condition of
for the first inequality. To prove Theorem 1.2, thanks to the doubling condition of  , which holds by use of the facts that
, which holds by use of the facts that  is nondecreasing and that
is nondecreasing and that  is nonincreasing, it suffices to show
is nonincreasing, it suffices to show

for all dyadic cubes  . Hereafter, we let
. Hereafter, we let

Let us define for 

and we will estimate

The case  and
and  We need the following crucial lemma, the proof of which is straightforward and is omitted (see [15, 16]).
We need the following crucial lemma, the proof of which is straightforward and is omitted (see [15, 16]).
Lemma 2.1.
For a nonnegative function  in
in  one lets
one lets  and
and  . For
. For  let
let

Considering the maximal cubes with respect to inclusion, one can write

where the cubes  are nonoverlapping. By virtue of the maximality of
are nonoverlapping. By virtue of the maximality of  one has that
one has that

Let

Then  is a disjoint family of sets which decomposes
is a disjoint family of sets which decomposes  and satisfies
and satisfies

Also, one sets

Then

With Lemma 2.1 in mind, let us return to the proof of Theorem 1.2. We need only to verify that

Inserting the definition of  , we have
, we have

Letting  , we will apply Lemma 2.1 to estimate this quantity. Retaining the same notation as Lemma 2.1 and noticing (2.13), we have
, we will apply Lemma 2.1 to estimate this quantity. Retaining the same notation as Lemma 2.1 and noticing (2.13), we have

We first evaluate

It follows from the definition of  that (2.17) is bounded by
that (2.17) is bounded by

By virtue of the support condition and (1.8) we have

If we invoke relations  and
and  , then (2.17) is bounded by
, then (2.17) is bounded by

Now that we have from the definition of the Morrey norm

we conclude that

Here, we have used the fact that  is nondecreasing, that
is nondecreasing, that  satisfies the doubling condition and that
satisfies the doubling condition and that

Similarly, we have

Summing up all factors, we obtain (2.14), by noticing that  is a disjoint family of sets which decomposes
is a disjoint family of sets which decomposes  .
.
The case  and
and  In this case we establish
In this case we establish

by the duality argument. Take a nonnegative function  ,
,  , satisfying that
, satisfying that  and that
and that

Letting  , we will apply Lemma 2.1 to estimation of this quantity. First, we will insert the definition of
, we will apply Lemma 2.1 to estimation of this quantity. First, we will insert the definition of  ,
,

First, we evaluate

Going through the same argument as the above, we see that (2.28) is bounded by

Using Hölder's inequality, we have

These yield

Similarly, we have

Summing up all factors we obtain

Another application of Hölder's inequality gives us that

Now that  , the maximal operator
, the maximal operator  is
is  -bounded. As a result we have
-bounded. As a result we have

This is our desired inequality.
The case  and
and  By a property of the dyadic cubes, for all
By a property of the dyadic cubes, for all  we have
we have

As a consequence we obtain

In view of the definition of  , for each
, for each  with
with  there exists a unique cube in
there exists a unique cube in  whose length is
whose length is  . Hence, inserting these estimates, we obtain
. Hence, inserting these estimates, we obtain

Here, in the last inequality we have used the doubling condition (1.8) and the facts that  ,
,  , and
, and  are nondecreasing and that
are nondecreasing and that  and
and  satisfy the doubling condition. Thus, we obtain
satisfy the doubling condition. Thus, we obtain

for all  . Inserting this pointwise estimate, we obtain
. Inserting this pointwise estimate, we obtain

This is our desired inequality.
2.2. Proof of Theorem 1.6
We need some lemmas.
Lemma 2.2 (see [1, Lemma 2.2]).
Let  . Suppose that
. Suppose that  satisfies (1.4), then
satisfies (1.4), then

Lemma 2.3.
Let  . Suppose that
. Suppose that  satisfies (1.4), then
satisfies (1.4), then

Proof.
Let  be a fixed point. For every cube
be a fixed point. For every cube  we see that
we see that

This implies

It follows from Lemma 2.2 that for every cube 

The desired inequality then follows.
Proof of Theorem 1.6.
We use definition (2.5) again and will estimate

for  .The case
.The case  In the course of the proof of Theorem 1.2, we have established (2.25)
In the course of the proof of Theorem 1.2, we have established (2.25)

We will use it with 

The case  It follows that
It follows that

from the Hölder inequality and the definition of the norm  . As a consequence we have
. As a consequence we have

Here, we have used the doubling condition (1.8) and the fact that  is nondecreasing in the third inequality. Hence it follows that
is nondecreasing in the third inequality. Hence it follows that

Combining (2.48) and (2.51), we obtain

We note that the assumption (1.24) implies  . Hence we arrive at the desired inequality by using Lemma 2.3.
. Hence we arrive at the desired inequality by using Lemma 2.3.
3. A Dual Version of Olsen's Inequality
In this section, as an application of Theorem 1.6, we consider a dual version of Olsen's inequality on predual of Morrey spaces (Theorem 3.1). As a corollary (Corollary 3.2), we have the boundedness properties of the operator  on predual of Morrey spaces. We will define the block spaces following [17].
on predual of Morrey spaces. We will define the block spaces following [17].
Let  and
and  . Suppose that
. Suppose that  satisfies (1.4). We say that a function
satisfies (1.4). We say that a function  on
on  is a
is a  -block provided that
-block provided that  is supported on a cube
is supported on a cube  and satisfies
and satisfies

The space  is defined by the set of all functions
is defined by the set of all functions  locally in
locally in  with the norm
with the norm

where each  is a
is a  -block and
-block and  , and the infimum is taken over all possible decompositions of
, and the infimum is taken over all possible decompositions of  . If
. If  ,
,  ,
,  is the usual block spaces, which we write for
is the usual block spaces, which we write for  and the norm for
and the norm for  , because the right-hand side of (3.1) is equal to
, because the right-hand side of (3.1) is equal to  . It is easy to prove
. It is easy to prove

when  . In [17, Theorem 1] and [18, Proposition 5], it was established that the predual space of
. In [17, Theorem 1] and [18, Proposition 5], it was established that the predual space of  is
is  . More precisely, if
. More precisely, if  , then
, then  is an element of
is an element of  . Conversely, any continuous linear functional in
. Conversely, any continuous linear functional in  can be realized with some
can be realized with some  .
.
Theorem 3.1.
Let  . Suppose that
. Suppose that  and
and  are nondecreasing but that
are nondecreasing but that  and
and  are nonincreasing. Suppose also that
are nonincreasing. Suppose also that

then

if  is a continuous function.
is a continuous function.
Theorem 3.1 generalizes [1, Theorem 3.1], and its proof is similar to that theorem, hence omitted. As a special case when  and
and  , we obtain the following.
, we obtain the following.
Corollary 3.2.
Let  . Suppose that
. Suppose that  is nondecreasing but that
is nondecreasing but that  is nonincreasing. Suppose also that
is nonincreasing. Suppose also that

then

We dare restate Corollary 3.2 in terms of the fractional integral operator  . The results hold by letting
. The results hold by letting  ,
,  ,
,  and
and  .
.
Proposition 3.3 (see [1, Proposition 3.8]).
Let  ,
,  , and
, and  . Suppose that
. Suppose that  ,
,  , and
, and  , then
, then

Remark 3.4 (see [1, Remark 3.9]).
In Proposition 3.3, if  is replaced by
is replaced by  , then, using the Hardy-Littlewood-Sobolev inequality locally and taking care of the larger scales by the same manner as the proof of Theorem 3.1, one has a naive bound for
, then, using the Hardy-Littlewood-Sobolev inequality locally and taking care of the larger scales by the same manner as the proof of Theorem 3.1, one has a naive bound for  .
.
References
Sawano Y, Sugano S, Tanaka H: Generalized fractional integral operators and fractional maximal operators in the framework of Morrey spaces. to appear in Trans. Amer. Math. Soc
Stein EM: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series. Volume 43. Princeton University Press, Princeton, NJ, USA; 1993:xiv+695.
Adams DR, Xiao J: Nonlinear potential analysis on Morrey spaces and their capacities. Indiana University Mathematics Journal 2004, 53(6):1629-1663.
Olsen PA: Fractional integration, Morrey spaces and a Schrödinger equation. Communications in Partial Differential Equations 1995, 20(11-12):2005-2055. 10.1080/03605309508821161
Sugano S, Tanaka H: Boundedness of fractional integral operators on generalized Morrey spaces. Scientiae Mathematicae Japonicae 2003, 58(3):531-540.
Eridani , Gunawan H: On generalized fractional integrals. Journal of the Indonesian Mathematical Society 2002, 8: 25-28.
Eridani , Gunawan H, Nakai E: On generalized fractional integral operators. Scientiae Mathematicae Japonicae 2004, 60(3):539-550.
Gunawan H: A note on the generalized fractional integral operators. Journal of the Indonesian Mathematical Society 2003, 9(1):39-43.
Nakai E: Generalized fractional integrals on Orlicz-Morrey spaces. In Banach and Function Spaces. Yokohama Publishers, Yokohama, Japan; 2004:323-333.
Nakai E: Orlicz-Morrey spaces and the Hardy-Littlewood maximal function. Studia Mathematica 2008, 188(3):193-221. 10.4064/sm188-3-1
Adams DR: A note on Riesz potentials. Duke Mathematical Journal 1975, 42(4):765-778. 10.1215/S0012-7094-75-04265-9
Fefferman CL: The uncertainty principle. Bulletin of the American Mathematical Society 1983, 9(2):129-206. 10.1090/S0273-0979-1983-15154-6
Kerman R, Sawyer E: The trace inequality and eigenvalue estimates for Schrödinger operators. Annales de l'Institut Fourier 1986, 36(4):207-228. 10.5802/aif.1074
Sawano Y, Sugano S, Tanaka H: Identification of the image of Morrey spaces by the fractional integral operators. Proceedings of A. Razmadze Mathematical Institute 2009, 149: 87-93.
Tanaka H: Morrey spaces and fractional operators. to appear in Journal of the Australian Mathematical Society
Pérez C:Sharp
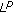 -weighted Sobolev inequalities. Annales de l'Institut Fourier 1995, 45(3):809-824. 10.5802/aif.1475
-weighted Sobolev inequalities. Annales de l'Institut Fourier 1995, 45(3):809-824. 10.5802/aif.1475Blasco O, Ruiz A, Vega L: Non-interpolation in Morrey-Campanato and block spaces. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1999, 28(1):31-40.
Zorko CT: Morrey space. Proceedings of the American Mathematical Society 1986, 98(4):586-592. 10.1090/S0002-9939-1986-0861756-X
Acknowledgments
The third author is supported by the Global COE program at Graduate School of Mathematical Sciences, University of Tokyo, and was supported by Fū jyukai foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sawano, Y., Sugano, S. & Tanaka, H. A Note on Generalized Fractional Integral Operators on Generalized Morrey Spaces. Bound Value Probl 2009, 835865 (2010). https://doi.org/10.1155/2009/835865
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/835865
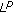 -weighted Sobolev inequalities. Annales de l'Institut Fourier 1995, 45(3):809-824. 10.5802/aif.1475
-weighted Sobolev inequalities. Annales de l'Institut Fourier 1995, 45(3):809-824. 10.5802/aif.1475