- Research Article
- Open access
- Published:
Infinitely Many Solutions of Strongly Indefinite Semilinear Elliptic Systems
Boundary Value Problems volume 2009, Article number: 865408 (2009)
Abstract
We proved a multiplicity result for strongly indefinite semilinear elliptic systems  in
in  ,
,  in
in  where
where  and
and  are positive numbers which are in the range we shall specify later.
are positive numbers which are in the range we shall specify later.
1. Introduction
In this paper, we shall study the existence of multiple solutions of the semilinear elliptic systems

where  and
and  are positive numbers which are in the range we shall specify later. Let us consider that the exponents
are positive numbers which are in the range we shall specify later. Let us consider that the exponents  ,
,  are below the critical hyperbola
are below the critical hyperbola

so one of  and
and  could be larger than
could be larger than  ; for that matter, the quadratic part of the energy functional
; for that matter, the quadratic part of the energy functional

has to be redefined, and we then need fractional Sobolev spaces.
Hence the energy functional  is strongly indefinite, and we shall use the generalized critical point theorem of Benci [1] in a version due to Heinz [2] to find critical points of
is strongly indefinite, and we shall use the generalized critical point theorem of Benci [1] in a version due to Heinz [2] to find critical points of  . And there is a lack of compactness due to the fact that we are working in
. And there is a lack of compactness due to the fact that we are working in  .
.
In [3], Yang shows that under some assumptions on the functions  and
and  there exist infinitely many solutions of the semilinear elliptic systems
there exist infinitely many solutions of the semilinear elliptic systems

We shall propose herein a result similar to [3] for problem (1.1).
2. Abstract Framework and Fractional Sobolev Spaces
We recall some abstract results developed in [4] or [5].
We shall work with space  , which are obtained as the domains of fractional powers of the operator
, which are obtained as the domains of fractional powers of the operator

Namely,  for
for  , and the corresponding operator is denoted by
, and the corresponding operator is denoted by  . The spaces
. The spaces  , the usual fractional Sobolev space
, the usual fractional Sobolev space  , are Hilbert spaces with inner product
, are Hilbert spaces with inner product

and associates norm

It is known that  is an isomorphism, and so we denote by
is an isomorphism, and so we denote by  the inverse of
the inverse of  .
.
Now let  ,
,  with
with  . We define the Hilbert space
. We define the Hilbert space  and the bilinear form
and the bilinear form  by the formula
by the formula

Using the Cauchy-Schwarz inequality, then it is easy to see that  is continuous and symmetric. Hence
is continuous and symmetric. Hence  induces a self-adjoint bounded linear operator
induces a self-adjoint bounded linear operator  such that
such that

Here and in what follows  denotes the inner product in
denotes the inner product in  induced by
induced by  and
and  on the product space
on the product space  in the usual way. It is easy to see that
in the usual way. It is easy to see that

We can then prove that  has two eigenvalues
has two eigenvalues  and
and  , whose corresponding eigenspaces are
, whose corresponding eigenspaces are

which give a natural splitting  . The spaces
. The spaces  and
and  are orthogonal with respect to the bilinear form
are orthogonal with respect to the bilinear form  , that is,
, that is,

We can also define the quadratic form  associated to
associated to  and
and  as
as

for all  . It follows then that
. It follows then that

where  ,
,  ,
,  . If
. If  , that is,
, that is,  , we have
, we have

Similarly

for  .
.
If  where
where  is a number satisfying the condition
is a number satisfying the condition

and  , it follows by (2.13) that
, it follows by (2.13) that  and by H
and by H lder inequalities that
lder inequalities that

In the sequel  denotes the norm in
denotes the norm in  , and we denote by
, and we denote by  the weighted function spaces with the norm defined on
the weighted function spaces with the norm defined on  by
by  . According to the properties of interpolation space, we have the following embedding theorem.
. According to the properties of interpolation space, we have the following embedding theorem.
Theorem 2.1.
Let  . one defines the operator
. one defines the operator  as follows: for
as follows: for  ,
,  ,
,

Then the inclusion of  into
into  is compact if
is compact if  .
.
Proof.
Observe that, by H lder's inequality and (2.14), we have
lder's inequality and (2.14), we have

where  ; hence
; hence  is well defined.
is well defined.
Then we will claim that  is compact. Since
is compact. Since  , for any
, for any  , there exists
, there exists  , such that
, such that  . Now, suppose
. Now, suppose  weakly in
weakly in  . We estimate
. We estimate

letting

we have

so that by H lder's inequality, we observe that, for any
lder's inequality, we observe that, for any  , we can choose a
, we can choose a  so that the integral over (
so that the integral over ( ) is smaller than
) is smaller than  for all
for all  , while for this fixed
, while for this fixed  , by strong convergence of
, by strong convergence of  to
to  in
in  on any bounded region, the integral over (
on any bounded region, the integral over ( ) is smaller than
) is smaller than  for
for  large enough. We thus have proved that
large enough. We thus have proved that  strongly in
strongly in  ; that is, the inclusion of
; that is, the inclusion of  into
into  is compact if
is compact if  .
.
3. Main Theorem
We consider below the problem of finding multiple solutions of the semilinear elliptic systems

Now if we choose  ,
,  ,
,  , such that
, such that

and we assume that
(H)  ,
,  and
and  and
and  are positive numbers such that
are positive numbers such that

We set

and we let

so that, under assumption (H), Theorem 2.1 holds, respectively, with  and
and  , and
, and  and
and  ; that is, the inclusion of
; that is, the inclusion of  into
into  and the inclusion of
and the inclusion of  into
into  are compact.
are compact.
If  , we let
, we let

denote the energy of  . It is well known that under assumption (H) the energy functional
. It is well known that under assumption (H) the energy functional  is well defined and continuously differentiable on
is well defined and continuously differentiable on  , and for all
, and for all  we have
we have


and it is also well known that the critical points of  are weak solutions of problem (3.1). The main theorem is the following.
are weak solutions of problem (3.1). The main theorem is the following.
Theorem 3.1.
Under assumption (H), problem (3.1) possesses infinitely many solutions  .
.
Since the functional  are strongly indefinite, a modified multiplicity critical points theorem Heinz [2] which is the generalized critical point theorem of Benci [1] will be used. For completeness, we state the result from here.
are strongly indefinite, a modified multiplicity critical points theorem Heinz [2] which is the generalized critical point theorem of Benci [1] will be used. For completeness, we state the result from here.
Theorem 3.2.
(see [2]) Let  be a real Hilbert space, and let
be a real Hilbert space, and let  be a functional with the following properties:
be a functional with the following properties:
(i)  has the form
has the form

where  is an invertible bounded self-adjoint linear operator in
is an invertible bounded self-adjoint linear operator in  and where
and where  is such that
is such that  and the gradient
and the gradient  is a compact operator;
is a compact operator;
(ii)  is even, that is
is even, that is  ;
;
(iii)  satisfies the Palais-Smale condition. Furthermore, let
satisfies the Palais-Smale condition. Furthermore, let

be an orthogonal splitting into  -invariant subspaces
-invariant subspaces  ,
,  such that
such that  . Then,
. Then,
-
(a)
suppose that there is an
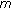 -dimensional linear subspace
-dimensional linear subspace 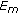 of
of  (
(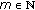 ) such that for the spaces
) such that for the spaces 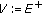 ,
,  one has
one has
(iv)  such that
such that  ,
,  ;
;
(v)  such that
such that  .Then there exist at least
.Then there exist at least  pairs
pairs  of critical points of
of critical points of  such that
such that  (
( );
);
-
(b)
a similar result holds when
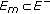 , and one takes
, and one takes  ,
, 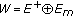 .
.
It is known from Section 2 that the operator  induced by the bilinear form
induced by the bilinear form  is an invertible bounded self-adjoint linear operator satisfying
is an invertible bounded self-adjoint linear operator satisfying  . We shall need some finite dimensional subspace of
. We shall need some finite dimensional subspace of  . Let
. Let  ,
,  ,
,  ,
, , be a complete orthogonal system in
, be a complete orthogonal system in  . Let
. Let  denote the finite dimensional subspaces of
denote the finite dimensional subspaces of  generated by
generated by  ,
,  ,
,  ,
, ,
, . Since
. Since  and
and  are isomorphisms, we know that
are isomorphisms, we know that  ,
,  ,
,  ,
, , is a complete orthogonal system in
, is a complete orthogonal system in  . Let
. Let  denote the finite dimensional subspaces of
denote the finite dimensional subspaces of  generated by
generated by  ,
,  ,
,  ,
, ,
, . For each
. For each  , we introduce the following subspaces of
, we introduce the following subspaces of  and
and 

Lemma 3.3.
The functional  defined in (3.6) satisfies conditions (ii), (iv), and (v) of Theorem 3.2.
defined in (3.6) satisfies conditions (ii), (iv), and (v) of Theorem 3.2.
Proof.
Condition (ii) is an immediate consequence of the definition of  . For condition (iv), by (2.11) and Theorem 2.1, for
. For condition (iv), by (2.11) and Theorem 2.1, for  ,
,

and since  ,
,  , we conclude that
, we conclude that  for
for  with
with  small.
small.
Next, let us prove condition (v). Let  be fixed, let
be fixed, let  , and write
, and write  and
and  . We have
. We have

Let  and
and  . Then we have
. Then we have  and
and  . Furthermore, we may write
. Furthermore, we may write  , where
, where  is orthogonal to
is orthogonal to  in
in  . We also have
. We also have  , where
, where  is orthogonal to
is orthogonal to  in
in  . It is easy to see that either
. It is easy to see that either  or
or  is positive. Suppose
is positive. Suppose  . Then we have
. Then we have

Using the fact that the norms in  are equivalent we obtain
are equivalent we obtain

with constant  independent of
independent of  . So from (3.13) and (2.11) we obtain
. So from (3.13) and (2.11) we obtain

The same arguments can be applied if  . So the result follows from (3.16).
. So the result follows from (3.16).
A sequence  is said to be the Palais-Smale sequence for
is said to be the Palais-Smale sequence for  (PS)-sequence for short) if
(PS)-sequence for short) if  uniformly in
uniformly in  and
and  in
in  . We say that
. We say that  satisfies the Palais-Smale condition (PS)-condition for short) if every (PS)-sequence of
satisfies the Palais-Smale condition (PS)-condition for short) if every (PS)-sequence of  is relatively compact in
is relatively compact in  .
.
Lemma 3.4.
Under assumption (H), the functional  satisfies the (PS)-condition.
satisfies the (PS)-condition.
Proof.
We first prove the boundedness of (PS)-sequences of  . Let
. Let  be a (PS)-sequence of
be a (PS)-sequence of  such that
such that


Taking  in (3.18), it follows from (3.17), (3.18), that
in (3.18), it follows from (3.17), (3.18), that

Next, we estimate  and
and  . From (3.18) with
. From (3.18) with  , we have
, we have

for all  . Using H
. Using H lder's inequality and by (3.20), we obtain
lder's inequality and by (3.20), we obtain

for all  , which implies that
, which implies that

Similarly, we prove that

Adding (3.22) and (3.23) we conclude that

Using this estimate in (3.19), we get

Since  and
and  , we conclude that both
, we conclude that both  and
and  are bounded, and consequently
are bounded, and consequently  and
and  are also bounded in terms of (3.24).
are also bounded in terms of (3.24).
Finally, we show that  contains a strongly convergent subsequence. It follows from
contains a strongly convergent subsequence. It follows from  and
and  which are bounded and Theorem 2.1 that
which are bounded and Theorem 2.1 that  contains a subsequence, denoted again by
contains a subsequence, denoted again by  , such that
, such that

It follows from (3.18) that

Therefore,


and by Theorem 2.1, we conclude that  strongly in
strongly in  and
and  strongly in
strongly in  .
.
Proof of Theorem 3.1.
Applying Lemmas 3.3 and 3.4 and Theorem 3.2, we can obtain the conclusion of Theorem 3.1.
References
Benci V: On critical point theory for indefinite functionals in the presence of symmetries. Transactions of the American Mathematical Society 1982, 274(2):533-572. 10.1090/S0002-9947-1982-0675067-X
Heinz H-P: Existence and gap-bifurcation of multiple solutions to certain nonlinear eigenvalue problems. Nonlinear Analysis: Theory, Methods & Applications 1993, 21(6):457-484. 10.1016/0362-546X(93)90128-F
Yang J: Multiple solutions of semilinear elliptic systems. Commentationes Mathematicae Universitatis Carolinae 1998, 39(2):257-268.
de Figueiredo DG, Felmer PL: On superquadratic elliptic systems. Transactions of the American Mathematical Society 1994, 343(1):99-116. 10.2307/2154523
de Figueiredo DG, Yang J: Decay, symmetry and existence of solutions of semilinear elliptic systems. Nonlinear Analysis: Theory, Methods & Applications 1998, 33(3):211-234. 10.1016/S0362-546X(97)00548-8
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, KJ. Infinitely Many Solutions of Strongly Indefinite Semilinear Elliptic Systems. Bound Value Probl 2009, 865408 (2009). https://doi.org/10.1155/2009/865408
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/865408
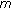 -dimensional linear subspace
-dimensional linear subspace 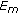 of
of  (
(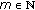 ) such that for the spaces
) such that for the spaces 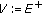 ,
,  one has
one has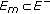 , and one takes
, and one takes  ,
, 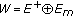 .
.