- Research Article
- Open access
- Published:
Homoclinic Solutions of Singular Nonautonomous Second-Order Differential Equations
Boundary Value Problems volume 2009, Article number: 959636 (2009)
Abstract
This paper investigates the singular differential equation  , having a singularity at
, having a singularity at  . The existence of a strictly increasing solution (a homoclinic solution) satisfying
. The existence of a strictly increasing solution (a homoclinic solution) satisfying  ,
,  is proved provided that
is proved provided that  has two zeros and a linear behaviour near
has two zeros and a linear behaviour near  .
.
1. Introduction
Having a positive parameter  we consider the problem
we consider the problem


under the following basic assumptions for  and
and 






Then problem (1.1), (1.2) generalizes some models arising in hydrodynamics or in the nonlinear field theory (see [1–5]). However (1.1) is singular at  because
because  .
.
Definition 1.1.
If  , thena solution of (1.1) on
, thena solution of (1.1) on  is a function
is a function  satisfying (1.1) on
satisfying (1.1) on  . If
. If  is a solution of (1.1) on
is a solution of (1.1) on  for each
for each  , then
, then  is a solution of (1.1) on
is a solution of (1.1) on  .
.
Definition 1.2.
Let  be a solution of (1.1) on
be a solution of (1.1) on  . If
. If  moreover fulfils conditions (1.2), it is called a solution of problem(1.1), (1.2).
moreover fulfils conditions (1.2), it is called a solution of problem(1.1), (1.2).
Clearly, the constant function  is a solution of problem (1.1), (1.2). An important question is the existence of a strictly increasing solution of (1.1), (1.2) because if such a solution exists, many important physical properties of corresponding models can be obtained. Note that if we extend the function
is a solution of problem (1.1), (1.2). An important question is the existence of a strictly increasing solution of (1.1), (1.2) because if such a solution exists, many important physical properties of corresponding models can be obtained. Note that if we extend the function  in (1.1) from the half–line onto
in (1.1) from the half–line onto  (as an even function), then any solution of (1.1), (1.2) has the same limit
(as an even function), then any solution of (1.1), (1.2) has the same limit  as
as  and
and  . Therefore we will use the following definition.
. Therefore we will use the following definition.
Definition 1.3.
A strictly increasing solution of problem (1.1), (1.2) is called a homoclinic solution.
Numerical investigation of problem (1.1), (1.2), where  and
and  ,
,  , can be found in [1, 4–6]. Problem (1.1), (1.2) can be also transformed onto a problem about the existence of a positive solution on the half-line. For
, can be found in [1, 4–6]. Problem (1.1), (1.2) can be also transformed onto a problem about the existence of a positive solution on the half-line. For  ,
,  and for
and for  ,
,  , such transformed problem was solved by variational methods in [7, 8], respectively. Some additional assumptions imposed on
, such transformed problem was solved by variational methods in [7, 8], respectively. Some additional assumptions imposed on  were needed there. Related problems were solved, for example, in [9, 10].
were needed there. Related problems were solved, for example, in [9, 10].
Here, we deal directly with problem (1.1), (1.2) and continue our earlier considerations of papers [11, 12], where we looked for additional conditions which together with (1.3)–(1.8) would guarantee the existence of a homoclinic solution.
Let us characterize some results reached in [11, 12] in more details. Both these papers assume (1.3)–(1.8). In [11] we study the case that  has at least three zeros
has at least three zeros  . More precisely, the conditions,
. More precisely, the conditions,

are moreover assumed. Then there exist  ,
,  and a solution
and a solution  of (1.1) on
of (1.1) on  such that
such that


We call such solution an escape solution. The main result of [11] is that (under (1.3)–(1.8), (1.9)) the set of solutions of (1.1), (1.10) for  consists of escape solutions and of oscillatory solutions (having values in
consists of escape solutions and of oscillatory solutions (having values in  ) and of at least one homoclinic solution. In [12] we omit assumptions (1.9) and prove that assumptions (1.3)–(1.8) are sufficient for the existence of an escape solution and also for the existence of a homoclinic solution provided the
) and of at least one homoclinic solution. In [12] we omit assumptions (1.9) and prove that assumptions (1.3)–(1.8) are sufficient for the existence of an escape solution and also for the existence of a homoclinic solution provided the  fulfils
fulfils

If (1.12) is not valid, then the existence of both an escape solution and a homoclinic solution is proved in [12], provided that  satisfies moreover
satisfies moreover


Assumption (1.13) characterizes the case that  has just two zeros
has just two zeros  and
and  in the interval
in the interval  . Further, we see that if (1.14) holds, then
. Further, we see that if (1.14) holds, then  is either bounded on
is either bounded on  or
or  is unbounded earlier and has a sublinear behaviour near
is unbounded earlier and has a sublinear behaviour near  .
.
This paper also deals with the case that  satisfies (1.13) and is unbounded above on
satisfies (1.13) and is unbounded above on  . In contrast to [12], here we prove the existence of a homoclinic solution for
. In contrast to [12], here we prove the existence of a homoclinic solution for  having a linear behaviour near
having a linear behaviour near  . The proof is based on a full description of the set of all solutions of problem (1.1), (1.10) for
. The proof is based on a full description of the set of all solutions of problem (1.1), (1.10) for  and on the existence of an escape solutions in this set.
and on the existence of an escape solutions in this set.
Finally, we want to mention the paper [13], where the problem

is investigated under the assumptions that  is continuous, it has three distinct zeros and satisfies the sign conditions similar to those in [11, (3.4)]. In [13], an approach quite different from [11, 12] is used. In particular, by means of properties of the associated vector field
is continuous, it has three distinct zeros and satisfies the sign conditions similar to those in [11, (3.4)]. In [13], an approach quite different from [11, 12] is used. In particular, by means of properties of the associated vector field  together with the Kneser's property of the cross sections of the solutions' funnel, the authors provide conditions which guarantee the existence of a strictly increasing solution of (1.15). The authors apply this general result to problem
together with the Kneser's property of the cross sections of the solutions' funnel, the authors provide conditions which guarantee the existence of a strictly increasing solution of (1.15). The authors apply this general result to problem

and get a strictly increasing solution of (1.16) for a sufficiently small  . This corresponds to the results of [11], where
. This corresponds to the results of [11], where  may be arbitrary.
may be arbitrary.
2. Initial Value Problem
In this section, under the assumptions (1.3)–(1.8) and (1.13) we prove some basic properties of solutions of the initial value problem (1.1), (1.10), where  .
.
Lemma 2.1.
For each  there exists a maximal
there exists a maximal  such that problem (1.1), (1.10) has a unique solution
such that problem (1.1), (1.10) has a unique solution  on
on  and
and

Further, for each  there exists
there exists  such that
such that

Proof.
Let  be a solution of problem (1.1), (1.10) on
be a solution of problem (1.1), (1.10) on  . By (1.1), we have
. By (1.1), we have

and multiplying by  and integrating between
and integrating between  and
and  , we get
, we get

Let  for some
for some  . Then (2.4) yields
. Then (2.4) yields  , which is not possible, because
, which is not possible, because  is decreasing on
is decreasing on  . Therefore
. Therefore  for
for  .
.
Let  . Consider the Banach space
. Consider the Banach space  (with the maximum norm) and an operator
(with the maximum norm) and an operator  defined by
defined by

A function  is a solution of problem (1.1), (1.2) on
is a solution of problem (1.1), (1.2) on  if and only if it is a fixed point of the operator
if and only if it is a fixed point of the operator  . Using the Lipschitz property of
. Using the Lipschitz property of  we can prove that the operator is contractive for each sufficiently small
we can prove that the operator is contractive for each sufficiently small  and from the Banach Fixed Point Theorem we conclude that there exists exactly one solution of problem (1.1), (1.2) on
and from the Banach Fixed Point Theorem we conclude that there exists exactly one solution of problem (1.1), (1.2) on  . This solution
. This solution  has the form
has the form

for  . Hence,
. Hence,  can be extended onto each interval
can be extended onto each interval  where
where  is bounded. So, we can put
is bounded. So, we can put  .
.
Let  . Then there exists
. Then there exists  such that
such that  for
for  . So, (2.6) yields
. So, (2.6) yields

Put

Then

and, by "per partes" integration we derive  . Multiplying (2.7) by
. Multiplying (2.7) by  and integrating it over
and integrating it over  , we get
, we get

Estimates (2.2) follow from (2.7)–(2.10) for

Remark 2.2.
The proof of Lemma 2.1 yields that if  , then
, then  .
.
Let us put

and consider an auxiliary equation

Similarly as in the proof of Lemma 2.1 we deduce that problem (2.13), (1.10) has a unique solution on  . Moreover the following lemma is true.
. Moreover the following lemma is true.
Lemma 2.3 ([12]).
For each  ,
,  and each
and each  , there exists
, there exists  such that for any
such that for any  ,
, 

Here  is a solution of problem (2.13), (1.10) with
is a solution of problem (2.13), (1.10) with  ,
,  .
.
Proof.
Choose  ,
,  ,
,  . Let
. Let  be the Lipschitz constant for
be the Lipschitz constant for  on
on  . By (2.6) for
. By (2.6) for  ,
,  ,
,  ,
,  ,
,

From the Gronwall inequality, we get

Similarly, by (2.6), (2.9), and (2.16),

If we choose  such that
such that

we get (2.14).
Remark 2.4.
Choose  and
and  , and consider the initial conditions
, and consider the initial conditions

Arguing as in the proof of Lemma 2.1, we get that problem (2.13), (2.19) has a unique solution on  . In particular, for
. In particular, for  and
and  , the unique solution of problem (2.13), (2.19) (and also of problem (1.1), (2.19)) is
, the unique solution of problem (2.13), (2.19) (and also of problem (1.1), (2.19)) is  and
and  , respectively.
, respectively.
Lemma 2.5.
Let  be a solution of problem (1.1), (1.10). Assume that there exists
be a solution of problem (1.1), (1.10). Assume that there exists  such that
such that

Then  for
for  and
and

Proof.
By (1.13) and (2.20),  on
on  and thus
and thus  and
and  are positive on
are positive on  . Consequently, there exists
. Consequently, there exists  . Further, by (1.1),
. Further, by (1.1),

and, by multiplication and integration over  ,
,

Therefore,

and hence  exists. Since
exists. Since  is bounded on
is bounded on  , we get
, we get

By (1.3), (1.8), and (2.22),  exists and, since
exists and, since  is bounded on
is bounded on  , we get
, we get  . Hence, letting
. Hence, letting  in (2.22), we obtain
in (2.22), we obtain  . Therefore,
. Therefore,  and (2.21) is proved.
and (2.21) is proved.
Lemma 2.6.
Let  be a solution of problem (1.1), (1.10). Assume that there exist
be a solution of problem (1.1), (1.10). Assume that there exist  and
and  such that
such that

Then  for all
for all  and (2.21) holds.
and (2.21) holds.
Proof.
Since  fulfils (2.26), we can find a maximal
fulfils (2.26), we can find a maximal  such that
such that  for
for  and consequently
and consequently  for
for  . By (4.23) and (2.26),
. By (4.23) and (2.26),  on
on  and thus
and thus  and
and  are negative on
are negative on  . So,
. So,  is positive and decreasing on
is positive and decreasing on  which yields
which yields  (otherwise, we get
(otherwise, we get  , contrary to (2.26)). Consequently there exists
, contrary to (2.26)). Consequently there exists  . By multiplication and integration (2.22) over
. By multiplication and integration (2.22) over  , we obtain
, we obtain

By similar argument as in the proof of Lemma 2.5 we get that  and
and  . Therefore (2.21) is proved.
. Therefore (2.21) is proved.
3. Damped Solutions
In this section, under assumptions (1.3)–(1.8) and (1.13) we describe a set of all damped solutions which are defined in the following way.
Definition 3.1.
A solution of problem (1.1), (1.10) (or of problem (2.13), (1.10)) on  is calleddamped if
is calleddamped if

Remark 3.2.
We see, by (2.12), that  is a damped solution of problem (1.1), (1.10) if and only if
is a damped solution of problem (1.1), (1.10) if and only if  is a damped solution of problem (2.13), (1.10). Therefore, we can borrow the arguments of [12] in the proofs of this section.
is a damped solution of problem (2.13), (1.10). Therefore, we can borrow the arguments of [12] in the proofs of this section.
Theorem 3.3.
If  is a damped solution of problem (1.1), (1.10), then
is a damped solution of problem (1.1), (1.10), then  has a finite number of isolated zeros and satisfies (2.21); or
has a finite number of isolated zeros and satisfies (2.21); or  is oscillatory (it has an unbounded set of isolated zeros).
is oscillatory (it has an unbounded set of isolated zeros).
Proof.
Let  be a damped solution of problem (1.1), (1.10). By Remark 2.2, we have
be a damped solution of problem (1.1), (1.10). By Remark 2.2, we have  in Lemma 2.1 and hence
in Lemma 2.1 and hence

Step 1.
If  has no zero in
has no zero in  , then
, then  for
for  and, by Lemma 2.5,
and, by Lemma 2.5,  fulfils (2.21).
fulfils (2.21).
Step 2.
Assume that  is the first zero of
is the first zero of  on
on  . Then, due to Remark 2.4,
. Then, due to Remark 2.4,  . Let
. Let  for
for  . By virtue of (1.4),
. By virtue of (1.4),  for
for  and thus
and thus  is decreasing. Let
is decreasing. Let  be positive on
be positive on  . Then
. Then  is also decreasing,
is also decreasing,  is increasing and
is increasing and  , due to (3.1). Consequently,
, due to (3.1). Consequently,  . Letting
. Letting  in (2.22), we get
in (2.22), we get  , which is impossible because
, which is impossible because  is bounded below. Therefore there are
is bounded below. Therefore there are  and
and  satisfying (2.26) and, by Lemma 2.6, either
satisfying (2.26) and, by Lemma 2.6, either  fulfils (2.21) or
fulfils (2.21) or  has the second zero
has the second zero  with
with  . So
. So  is positive on
is positive on  and has just one local maximum
and has just one local maximum  in
in  . Moreover, putting
. Moreover, putting  and
and  in (2.23), we have
in (2.23), we have

and hence

Step 3.
Let  have no other zeros. Then
have no other zeros. Then  for
for  . Assume that
. Assume that  is negative on
is negative on  . Then, due to (2.1),
. Then, due to (2.1),  . Putting
. Putting  in (2.23) and letting
in (2.23) and letting  , we obtain
, we obtain

Therefore,  exists and, since
exists and, since  is bounded, we deduce that
is bounded, we deduce that

Letting  in (2.22), we get
in (2.22), we get  , which contradicts the fact that
, which contradicts the fact that  is bounded above. Therefore,
is bounded above. Therefore,  cannot be negative on the whole interval
cannot be negative on the whole interval  and there exists
and there exists  such that
such that  . Moreover, according to (3.2),
. Moreover, according to (3.2),  .
.
Then, Lemma 2.5 yields that  fulfils (2.21). Since
fulfils (2.21). Since  is positive on
is positive on  ,
,  has just one minimum
has just one minimum  on
on  . Moreover, putting
. Moreover, putting  and
and  in (2.23), we have
in (2.23), we have

which together with (3.4) yields

Step 4.
Assume that  has its third zero
has its third zero  . Then we prove as in Step 2 that
. Then we prove as in Step 2 that  has just one negative minimum
has just one negative minimum  in
in  and (3.8) is valid. Further, as in Step 2, we deduce that either
and (3.8) is valid. Further, as in Step 2, we deduce that either  fulfils (2.21) or
fulfils (2.21) or  has the fourth zero
has the fourth zero  ,
,  is positive on
is positive on  with just one local maximum
with just one local maximum  on
on  , and
, and  . This together with (3.8) yields
. This together with (3.8) yields

If  has no other zeros, we deduce as in Step 3 that
has no other zeros, we deduce as in Step 3 that  has just one negative minimum
has just one negative minimum  in
in  ,
,  and
and  fulfils (2.21).
fulfils (2.21).
Step 5.
If  has other zeros, we use the previous arguments and get that either
has other zeros, we use the previous arguments and get that either  has a finite number of zeros and then fulfils (2.21) or
has a finite number of zeros and then fulfils (2.21) or  is oscillatory.
is oscillatory.
Remark 3.4.
According to the proof of Theorem 3.3, we see that if  is oscillatory, it has just one positive local maximum between the first and the second zero, then just one negative local minimum between the second and the third zero, and so on. By (3.8), (3.9), (1.4)–(1.6) and (1.13), these maxima are decreasing (minima are increasing) for
is oscillatory, it has just one positive local maximum between the first and the second zero, then just one negative local minimum between the second and the third zero, and so on. By (3.8), (3.9), (1.4)–(1.6) and (1.13), these maxima are decreasing (minima are increasing) for  increasing.
increasing.
Lemma 3.5.
A solution  of problem (1.1), (1.10) fulfils the condition
of problem (1.1), (1.10) fulfils the condition

if and only if  fulfils the condition
fulfils the condition

Proof.
Assume that  fulfils (3.10). Then there exists
fulfils (3.10). Then there exists  such that
such that  ,
,  for
for  . Otherwise
. Otherwise  , due to Lemma 2.5. Let
, due to Lemma 2.5. Let  be such that
be such that  on
on  ,
,  . By Remark 2.4 and (3.10),
. By Remark 2.4 and (3.10),  . Integrating (1.1) over
. Integrating (1.1) over  , we get
, we get

Due to (1.4), we see that  is strictly decreasing for
is strictly decreasing for  as long as
as long as  . Thus, there are two possibilities. If
. Thus, there are two possibilities. If  for all
for all  , then from Lemma 2.6 we get (2.21), which contradicts (3.10). If there exists
, then from Lemma 2.6 we get (2.21), which contradicts (3.10). If there exists  such that
such that  , then in view Remark 2.4 we have
, then in view Remark 2.4 we have  . Using the arguments of Steps 3–5 of the proof of Theorem 3.3, we get that
. Using the arguments of Steps 3–5 of the proof of Theorem 3.3, we get that  is damped, contrary to (3.10). Therefore, such
is damped, contrary to (3.10). Therefore, such  cannot exist and
cannot exist and  on
on  . Consequently,
. Consequently,  . So,
. So,  fulfils (3.11). The inverse implication is evident.
fulfils (3.11). The inverse implication is evident.
Remark 3.6.
According to Definition 1.3 and Lemma 3.5,  is a homoclinic solution of problem (1.1), (1.10) if and only if
is a homoclinic solution of problem (1.1), (1.10) if and only if  is a homoclinic solution of problem (2.13), (1.10).
is a homoclinic solution of problem (2.13), (1.10).
Theorem 3.7 (on damped solutions).
Let  satisfy (1.5) and (1.6). Assume that
satisfy (1.5) and (1.6). Assume that  is a solution of problem (1.1), (1.10) with
is a solution of problem (1.1), (1.10) with  . Then
. Then  is damped.
is damped.
Proof.
Let  be a solution of (1.1), (1.10) with
be a solution of (1.1), (1.10) with  . Then, by (1.4)–(1.6),
. Then, by (1.4)–(1.6),

Assume on the contrary that  is not damped. Then
is not damped. Then  is defined on the interval
is defined on the interval  and
and  or there exists
or there exists  such that
such that  ,
,  and
and  for
for  . If the latter possibility occurs, (2.22) and (3.13) give by integration
. If the latter possibility occurs, (2.22) and (3.13) give by integration

a contradiction. If  , then, by Lemma 3.5,
, then, by Lemma 3.5,  fulfils (3.11). So
fulfils (3.11). So  has a unique zero
has a unique zero  . Integrating (2.22) over
. Integrating (2.22) over  , we get
, we get

and so

Integrating (2.22) over  , we obtain for
, we obtain for 

Therefore,  on
on  , and letting
, and letting  , we get
, we get  . This together with (3.16) contradicts (3.13). We have proved that
. This together with (3.16) contradicts (3.13). We have proved that  is damped.
is damped.
Theorem 3.8.
Let  be the set of all
be the set of all  such that corresponding solutions of problem (1.1), (1.10) are damped. Then
such that corresponding solutions of problem (1.1), (1.10) are damped. Then  is open in
is open in  .
.
Proof.
Let  and
and  be a solution of (1.1), (1.10) with
be a solution of (1.1), (1.10) with  . So,
. So,  is damped and
is damped and  is also a solution of (2.13).
is also a solution of (2.13).
-
(a)
Let
 be oscillatory. Then its first local maximum belongs to
be oscillatory. Then its first local maximum belongs to  . Lemma 2.3 guarantees that if
. Lemma 2.3 guarantees that if 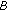 is sufficiently close to
is sufficiently close to 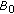 , the corresponding solution
, the corresponding solution  of (2.13), (1.10) has also its first local maximum in
of (2.13), (1.10) has also its first local maximum in  . This means that there exist
. This means that there exist 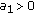 and
and 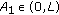 such that
such that  satisfies (2.26). Now, we can continue as in the proof of Theorem 3.3 using the arguments of Steps 2–5 and Remark 3.2 to get that
satisfies (2.26). Now, we can continue as in the proof of Theorem 3.3 using the arguments of Steps 2–5 and Remark 3.2 to get that  is damped.
is damped. -
(b)
Let
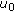 have at most a finite number of zeros. Then, by Theorem 3.3,
have at most a finite number of zeros. Then, by Theorem 3.3, 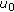 fulfils (2.21). Choose
fulfils (2.21). Choose  . Since
. Since  fulfils (2.22), we get by integration over
fulfils (2.22), we get by integration over 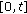
 (3.18)
(3.18)
For  we get, by (2.21),
we get, by (2.21),

Therefore, we can find  such that
such that

Let  be the constant of Lemma 2.1. Choose
be the constant of Lemma 2.1. Choose  . Assume that
. Assume that  and
and  is a corresponding solution of problem (2.13), (1.10). Using Lemma 2.1, Lemma 2.3 and the continuity of
is a corresponding solution of problem (2.13), (1.10). Using Lemma 2.1, Lemma 2.3 and the continuity of  , we can find
, we can find  such that if
such that if  , then
, then

moreover  for
for  and
and

Therefore, we have

Consequently, integrating (2.13) over  and using (3.19)–(3.23), we get for
and using (3.19)–(3.23), we get for 

We get  for
for  . Therefore,
. Therefore,  for
for  and, due to (1.4)–(1.6),
and, due to (1.4)–(1.6),

Assume that there is  such that
such that  ,
,  . Then, since
. Then, since  if
if  and
and  , we get
, we get  and
and  for
for  , contrary to (3.25). Hence we get that
, contrary to (3.25). Hence we get that  fulfils (3.1).
fulfils (3.1).
4. Escape Solutions
During the whole section, we assume (1.3)–(1.8) and (1.13). We prove that problem (1.1), (1.10) has at least one escape solution. According to Section 1 and Remark 2.2, we work with the following definitions.
Definition 4.1.
Let  . A solution of problem (1.1), (1.10) on
. A solution of problem (1.1), (1.10) on  is called an escape solution if
is called an escape solution if

Definition 4.2.
A solution  of problem (2.13), (1.10) is called an escape solution, if there exists
of problem (2.13), (1.10) is called an escape solution, if there exists  such that
such that

Remark 4.3.
If  is an escape solution of problem (2.13), (1.10), then
is an escape solution of problem (2.13), (1.10), then  is an escape solution of problem (1.1), (1.10) on some interval
is an escape solution of problem (1.1), (1.10) on some interval  .
.
Theorem 4.4 (on three types of solutions.).
Let  be a solution of problem (1.1), (1.10). Then
be a solution of problem (1.1), (1.10). Then  is just one of the following three types
is just one of the following three types
(I) is damped;
is damped;
(II) is homoclinic;
is homoclinic;
(III) is escape.
is escape.
Proof.
By Definition 3.1,  is damped if and only if (3.1) holds. By Lemma 3.5 and Definition 1.3,
is damped if and only if (3.1) holds. By Lemma 3.5 and Definition 1.3,  is homoclinic if and only if (3.10) holds. Let
is homoclinic if and only if (3.10) holds. Let  be neither damped nor homoclinic. Then there exists
be neither damped nor homoclinic. Then there exists  such that
such that  is bounded on
is bounded on  ,
,  ,
,  . So,
. So,  has its first zero
has its first zero  and
and  on
on  . Assume that there exist
. Assume that there exist  such that
such that  and
and  . Then, by Lemma 2.6, either
. Then, by Lemma 2.6, either  fulfils (2.21) or
fulfils (2.21) or  has its second zero and, arguing as in Steps 2–5 of the proof of Theorem 3.3, we deduce that
has its second zero and, arguing as in Steps 2–5 of the proof of Theorem 3.3, we deduce that  is a damped solution. This contradiction implies that
is a damped solution. This contradiction implies that  on
on  . Therefore, by Definition 4.1,
. Therefore, by Definition 4.1,  is an escape solution.
is an escape solution.
Theorem 4.5.
Let  be the set of all
be the set of all  such that the corresponding solutions of (1.1), (1.10) are escape solutions. The set
such that the corresponding solutions of (1.1), (1.10) are escape solutions. The set  is open in
is open in  .
.
Proof.
Let  and
and  be a solution of problem (1.1), (1.10) with
be a solution of problem (1.1), (1.10) with  . So,
. So,  fulfils (4.1) for some
fulfils (4.1) for some  . Let
. Let  be a solution of problem (2.13), (1.10) with
be a solution of problem (2.13), (1.10) with  . Then
. Then  on
on  and
and  is increasing on
is increasing on  . There exists
. There exists  and
and  such that
such that  . Let
. Let  be a solution of problem (2.13), (1.10) for some
be a solution of problem (2.13), (1.10) for some  . Lemma 2.3 yields
. Lemma 2.3 yields  such that if
such that if  , then
, then  . Therefore,
. Therefore,  is an escape solution of problem (2.13), (1.10). By Remark 4.3,
is an escape solution of problem (2.13), (1.10). By Remark 4.3,  is also an escape solution of problem (1.1), (1.10) on some interval
is also an escape solution of problem (1.1), (1.10) on some interval  .
.
To prove that the set  of Theorem 4.5 is nonempty we will need the following two lemmas.
of Theorem 4.5 is nonempty we will need the following two lemmas.
Lemma 4.6.
Let  . Assume that
. Assume that  is a solution of problem (1.1), (1.10) on
is a solution of problem (1.1), (1.10) on  and
and  is a maximal interval where
is a maximal interval where  is increasing and
is increasing and  for
for  . Then
. Then

Proof.
Step 1.
We show that the interval  is nonempty. Since
is nonempty. Since  and
and  satisfies (1.3), (1.13), we can find
satisfies (1.3), (1.13), we can find  such that
such that

Integrating (1.1) over  we obtain
we obtain

So,  is an increasing solution of problem (1.1), (1.10) on
is an increasing solution of problem (1.1), (1.10) on  and
and  for
for  . Therefore the nonempty interval
. Therefore the nonempty interval  exists.
exists.
Step 2.
By multiplication of (1.1) by  and integration over
and integration over  we obtain
we obtain

Using the "per partes" integration, we get for 

This relation together with (4.6) implies (4.3).
Remark 4.7.
Consider a solution  of Lemma 4.6. If
of Lemma 4.6. If  is an escape solution, then
is an escape solution, then  . Assume that
. Assume that  is not an escape solution. Then both possibilities
is not an escape solution. Then both possibilities  and
and  can occur. Let
can occur. Let  . By Theorem 4.4 and Lemma 2.5,
. By Theorem 4.4 and Lemma 2.5,  ,
,  . Let
. Let  . We write
. We write  ,
,  . Using Lemmas 3.5 and 2.5 and Theorem 4.4, we obtain
. Using Lemmas 3.5 and 2.5 and Theorem 4.4, we obtain  and either
and either  or
or  .
.
Lemma 4.8.
Let  and let
and let  . Then for each
. Then for each 
(i)there exists a solution  of problem (1.1), (1.10) with
of problem (1.1), (1.10) with  ,
,
(ii)there exists  such that
such that  is the maximal interval on which the solution
is the maximal interval on which the solution  is increasing and its values in this interval are contained in
is increasing and its values in this interval are contained in  ,
,
(iii)there exists  satisfying
satisfying  .
.
If the sequence  is unbounded, then there exists
is unbounded, then there exists  such that
such that  is an escape solution.
is an escape solution.
Proof.
Similar arugmets can be found in [12]. By Lemma 2.1, the assertion (i) holds. The arguments in Step 1 of the proof of Lemma 4.6 imply (ii). The strict monotonicity of  and Remark 4.7 yields a unique
and Remark 4.7 yields a unique  . Assume that
. Assume that  is unbounded. Then
is unbounded. Then

(otherwise, we take a subsequence). Assume on the contrary that for any  ,
,  is not an escape solution. Choose
is not an escape solution. Choose  . Then, by Remark 4.7,
. Then, by Remark 4.7,

Due to (4.9), (1.2) and (ii) there exists  satisfying
satisfying

By (i) and (ii),  satisfies
satisfies

Integrating it over  we get
we get

Put

Then, by (4.12),

We see that  is decreasing. From (1.4) and (1.6) we get that
is decreasing. From (1.4) and (1.6) we get that  is increasing on
is increasing on  and consequently by (4.9) and (4.13), we have
and consequently by (4.9) and (4.13), we have

Integrating (4.14) over  and using (4.10), we obtain
and using (4.10), we obtain

where

Further, by (4.15),


Conditions (1.8) and (4.8) yield  , which implies
, which implies

By (4.13) and (4.18),

and consequently

which contradicts (4.20). Therefore, at least one escape solution of (1.1), (1.10) with  must exist.
must exist.
Theorem 4.9 (on escape solution).
Assume that (1.3)–(1.8) and (1.13) hold and let

Then there exists  such that the corresponding solution of problem (1.1), (1.10) is an escape solution.
such that the corresponding solution of problem (1.1), (1.10) is an escape solution.
Proof.
Let  and let
and let  ,
,  ,
,  and
and  be sequences from Lemma 4.8. Moreover, let
be sequences from Lemma 4.8. Moreover, let

By (4.24) we can find  such that
such that  for
for  . We assume that for any
. We assume that for any  ,
,  is not an escape solution and we construct a contradiction.
is not an escape solution and we construct a contradiction.
Step 1.
We derive some inequality for  . By Remark 4.7, we have
. By Remark 4.7, we have

and, by Lemma 4.8, the sequence  is bounded. Therefore there exists
is bounded. Therefore there exists  such that
such that

Choose an arbitrary  . According to Lemma 4.6,
. According to Lemma 4.6,  satisfies equality (4.3), that is
satisfies equality (4.3), that is

Since  and
and  is increasing on
is increasing on  , there exists a unique
, there exists a unique  such that
such that

Having in mind, due to (1.4)–(1.8), that the inequality

holds, we get

By virtue of (1.6) and (1.13), we see that  is decreasing on
is decreasing on  , which yields
, which yields

Hence,

Since  and
and  , the monotonicity of
, the monotonicity of  yields
yields  for
for  , and consequently
, and consequently

Therefore (4.27) and (4.32) give

Step 2.
We prove that the sequence  is bounded below by some positive number. Since
is bounded below by some positive number. Since  is a solution of (1.1) on
is a solution of (1.1) on  , we have
, we have

Integrating it, we get

where  satisfies
satisfies  and
and  . Having in mind (1.8), we see that
. Having in mind (1.8), we see that  is increasing and
is increasing and  for
for  . Consequently
. Consequently

Integrating (4.36) over  , we obtain
, we obtain

and hence

By (4.23) we get

which, due to (4.39), yields

So, by virtue of (4.37), there exists  such that
such that  for
for  .
.
Step 3.
We construct a contradiction. Putting  in (4.34), we have
in (4.34), we have

Due to (4.23),  . Therefore,
. Therefore,  , and consequently, by (4.24),
, and consequently, by (4.24),

In order to get a contradiction, we distinguish two cases.
Case 1.
Let  , that is, we can find
, that is, we can find  ,
,  ,
,  , such that
, such that

Then, by (4.43), for each sufficiently large  , we get
, we get

Putting it to (4.42), we have

Therefore  , contrary to (4.25).
, contrary to (4.25).
Case 2.
Let  . We may assume
. We may assume  (otherwise we take a subsequence). Then there exists
(otherwise we take a subsequence). Then there exists  ,
,  , such that
, such that

Due to (4.43), for each sufficiently large  , we get
, we get

Putting it to (4.42), we have

Therefore,  for
for  . Integrating it over
. Integrating it over  , we obtain
, we obtain

which yields, by (4.26),  and also
and also  , contrary to (4.25). These contradictions obtained in both cases imply that there exists
, contrary to (4.25). These contradictions obtained in both cases imply that there exists  such that
such that  is an escape solution.
is an escape solution.
5. Homoclinic Solution
The following theorem provides the existence of a homoclinic solution under the assumption that the function  in (1.1) has a linear behaviour near
in (1.1) has a linear behaviour near  . According to Definition 1.2, a homoclinic solution is a strictly increasing solution of problem (1.1), (1.2).
. According to Definition 1.2, a homoclinic solution is a strictly increasing solution of problem (1.1), (1.2).
Theorem 5.1 (On homoclinic solution.).
Let the assumptions of Theorem 4.9 be satisfied. Then there exists  such that the corresponding solution of problem (1.1), (1.10) is a homoclinic solution.
such that the corresponding solution of problem (1.1), (1.10) is a homoclinic solution.
Proof.
For  denote by
denote by  the corresponding solution of problem (1.1), (1.10). Let
the corresponding solution of problem (1.1), (1.10). Let  and
and  be the set of all
be the set of all  such that
such that  is a damped solution and an escape solution, respectively. By Theorems 3.7, 3.8, 4.5, and 4.9, the sets
is a damped solution and an escape solution, respectively. By Theorems 3.7, 3.8, 4.5, and 4.9, the sets  and
and  are nonempty and open in
are nonempty and open in  . Therefore, the set
. Therefore, the set  is nonempty. Choose
is nonempty. Choose  . Then, by Theorem 4.4,
. Then, by Theorem 4.4,  is a homoclinic solution. Moreover, due to Theorem 3.7,
is a homoclinic solution. Moreover, due to Theorem 3.7,  .
.
Example 5.2.
The function

where  is a negative constant, satisfies the conditions (1.3)–(1.6), (1.13), and (4.23).
is a negative constant, satisfies the conditions (1.3)–(1.6), (1.13), and (4.23).
References
Dell'Isola F, Gouin H, Rotoli G: Nucleation of spherical shell-like interfaces by second gradient theory: numerical simulations. European Journal of Mechanics. B 1996, 15(4):545-568.
Derrick GH: Comments on nonlinear wave equations as models for elementary particles. Journal of Mathematical Physics 1964, 5: 1252-1254. 10.1063/1.1704233
Gouin H, Rotoli G: An analytical approximation of density profile and surface tension of microscopic bubbles for Van Der Waals fluids. Mechanics Research Communications 1997, 24(3):255-260. 10.1016/S0093-6413(97)00022-0
Kitzhofer G, Koch O, Lima P, Weinmüller E: Efficient numerical solution of the density profile equation in hydrodynamics. Journal of Scientific Computing 2007, 32(3):411-424. 10.1007/s10915-007-9141-0
Lima PM, Konyukhova NB, Sukov AI, Chemetov NV: Analytical-numerical investigation of bubble-type solutions of nonlinear singular problems. Journal of Computational and Applied Mathematics 2006, 189(1-2):260-273. 10.1016/j.cam.2005.05.004
Koch O, Kofler P, Weinmüller EB: Initial value problems for systems of ordinary first and second order differential equations with a singularity of the first kind. Analysis 2001, 21(4):373-389.
Bonheure D, Gomes JM, Sanchez L: Positive solutions of a second-order singular ordinary differential equation. Nonlinear Analysis: Theory, Methods & Applications 2005, 61(8):1383-1399. 10.1016/j.na.2005.02.029
Conti M, Merizzi L, Terracini S:Radial solutions of superlinear equations on
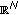 . I. A global variational approach. Archive for Rational Mechanics and Analysis 2000, 153(4):291-316. 10.1007/s002050050015
. I. A global variational approach. Archive for Rational Mechanics and Analysis 2000, 153(4):291-316. 10.1007/s002050050015Berestycki H, Lions P-L, Peletier LA:An ODE approach to the existence of positive solutions for semilinear problems in
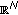 . Indiana University Mathematics Journal 1981, 30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981, 30(1):141-157. 10.1512/iumj.1981.30.30012Maatoug L: On the existence of positive solutions of a singular nonlinear eigenvalue problem. Journal of Mathematical Analysis and Applications 2001, 261(1):192-204. 10.1006/jmaa.2001.7491
Rachůnková I, Tomeček J: Singular nonlinear problem for ordinary differential equation of the second-order on the half-line. In Mathematical Models in Engineering, Biology and Medicine: International Conference on Boundary Value Problems Edited by: Cabada A, Liz E, Nieto JJ. 2009, 294-303.
Rachůnková I, Tomeček J: Bubble-type solutions of nonlinear singular problem. submitted
Palamides AP, Yannopoulos TG: Terminal value problem for singular ordinary differential equations: theoretical analysis and numerical simulations of ground states. Boundary Value Problems 2006, 2006:-28.
Acknowledgments
The authors thank the referee for valuable comments. This work was supported by the Council of Czech Government MSM 6198959214.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rachůnková, I., Tomeček, J. Homoclinic Solutions of Singular Nonautonomous Second-Order Differential Equations. Bound Value Probl 2009, 959636 (2009). https://doi.org/10.1155/2009/959636
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/959636
 be oscillatory. Then its first local maximum belongs to
be oscillatory. Then its first local maximum belongs to  . Lemma 2.3 guarantees that if
. Lemma 2.3 guarantees that if 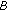 is sufficiently close to
is sufficiently close to 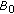 , the corresponding solution
, the corresponding solution  of (2.13), (1.10) has also its first local maximum in
of (2.13), (1.10) has also its first local maximum in  . This means that there exist
. This means that there exist 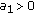 and
and 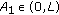 such that
such that  satisfies (2.26). Now, we can continue as in the proof of Theorem 3.3 using the arguments of Steps 2–5 and Remark 3.2 to get that
satisfies (2.26). Now, we can continue as in the proof of Theorem 3.3 using the arguments of Steps 2–5 and Remark 3.2 to get that  is damped.
is damped.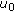 have at most a finite number of zeros. Then, by Theorem 3.3,
have at most a finite number of zeros. Then, by Theorem 3.3, 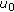 fulfils (2.21). Choose
fulfils (2.21). Choose  . Since
. Since  fulfils (2.22), we get by integration over
fulfils (2.22), we get by integration over 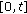

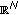 . I. A global variational approach. Archive for Rational Mechanics and Analysis 2000, 153(4):291-316. 10.1007/s002050050015
. I. A global variational approach. Archive for Rational Mechanics and Analysis 2000, 153(4):291-316. 10.1007/s002050050015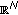 . Indiana University Mathematics Journal 1981, 30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981, 30(1):141-157. 10.1512/iumj.1981.30.30012