- Research Article
- Open access
- Published:
Positive Solutions of Singular Multipoint Boundary Value Problems for Systems of Nonlinear Second-Order Differential Equations on Infinite Intervals in Banach Spaces
Boundary Value Problems volume 2009, Article number: 978605 (2009)
Abstract
The cone theory together with Mönch fixed point theorem and a monotone iterative technique is used to investigate the positive solutions for some boundary problems for systems of nonlinear second-order differential equations with multipoint boundary value conditions on infinite intervals in Banach spaces. The conditions for the existence of positive solutions are established. In addition, an explicit iterative approximation of the solution for the boundary value problem is also derived.
1. Introduction
In recent years, the theory of ordinary differential equations in Banach space has become a new important branch of investigation (see, e.g., [1–4] and references therein). By employing a fixed point theorem due to Sadovskii, Liu [5] investigated the existence of solutions for the following second-order two-point boundary value problems (BVP for short) on infinite intervals in a Banach space  :
:

where  On the other hand, the multipoint boundary value problems arising naturally from applied mathematics and physics have been studied so extensively in scalar case that there are many excellent results about the existence of positive solutions (see, i.e., [6–12] and references therein). However, to the best of our knowledge, only a few authors [5, 13, 14] have studied multipoint boundary value problems in Banach spaces and results for systems of second-order differential equation are rarely seen. Motivated by above papers, we consider the following singular
On the other hand, the multipoint boundary value problems arising naturally from applied mathematics and physics have been studied so extensively in scalar case that there are many excellent results about the existence of positive solutions (see, i.e., [6–12] and references therein). However, to the best of our knowledge, only a few authors [5, 13, 14] have studied multipoint boundary value problems in Banach spaces and results for systems of second-order differential equation are rarely seen. Motivated by above papers, we consider the following singular  -point boundary value problem on an infinite interval in a Banach space
-point boundary value problem on an infinite interval in a Banach space 

where  and
and  with
with  In this paper, nonlinear terms
In this paper, nonlinear terms  and
and  may be singular at
may be singular at  , and/or
, and/or  , where
, where  denotes the zero element of Banach space
denotes the zero element of Banach space  . By singularity, we mean that
. By singularity, we mean that  as
as  or
or 
Very recently, by using Shauder fixed point theorem, Guo [15] obtained the existence of positive solutions for a class of  th-order nonlinear impulsive singular integro-differential equations in a Banach space. Motivated by Guo's work, in this paper, we will use the cone theory and the Mönch fixed point theorem combined with a monotone iterative technique to investigate the positive solutions of BVP (1.2). The main features of the present paper are as follows. Firstly, compared with [5], the problem we discussed here is systems of multipoint boundary value problem and nonlinear term permits singularity not only at
th-order nonlinear impulsive singular integro-differential equations in a Banach space. Motivated by Guo's work, in this paper, we will use the cone theory and the Mönch fixed point theorem combined with a monotone iterative technique to investigate the positive solutions of BVP (1.2). The main features of the present paper are as follows. Firstly, compared with [5], the problem we discussed here is systems of multipoint boundary value problem and nonlinear term permits singularity not only at  but also at
but also at  . Secondly, compared with [15], the relative compact conditions we used are weaker. Furthermore, an iterative sequence for the solution under some normal type conditions is established which makes it very important and convenient in applications.
. Secondly, compared with [15], the relative compact conditions we used are weaker. Furthermore, an iterative sequence for the solution under some normal type conditions is established which makes it very important and convenient in applications.
The rest of the paper is organized as follows. In Section 2, we give some preliminaries and establish several lemmas. The main theorems are formulated and proved in Section 3. Then, in Section 4, an example is worked out to illustrate the main results.
2. Preliminaries and Several Lemmas
Let

Evidently,  . It is easy to see that
. It is easy to see that  is a Banach space with norm
is a Banach space with norm

and  is also a Banach space with norm
is also a Banach space with norm

where

Let  with norm
with norm

Then  is also a Banach space. The basic space using in this paper is
is also a Banach space. The basic space using in this paper is  .
.
Let  be a normal cone in
be a normal cone in  with normal constant
with normal constant  which defines a partial ordering in
which defines a partial ordering in  by
by  . If
. If  and
and  , we write
, we write  . Let
. Let  . So,
. So,  if and only if
if and only if  . For details on cone theory, see [4].
. For details on cone theory, see [4].
In what follows, we always assume that  . Let
. Let  . Obviously,
. Obviously,  for any
for any  . When
. When  , we write
, we write  , that is,
, that is,  . Let
. Let  and
and  . It is clear,
. It is clear,  are cones in
are cones in  and
and  , respectively. A map
, respectively. A map  is called a positive solution of BVP (1.2) if
is called a positive solution of BVP (1.2) if  and
and  satisfies (1.2).
satisfies (1.2).
Let  denote the Kuratowski measure of noncompactness in
denote the Kuratowski measure of noncompactness in  and
and  , respectively. For details on the definition and properties of the measure of noncompactness, the reader is referred to [1–4]. Let
, respectively. For details on the definition and properties of the measure of noncompactness, the reader is referred to [1–4]. Let  be all Lebesgue measurable functions from
be all Lebesgue measurable functions from  to
to  . Denote
. Denote

Let us list some conditions for convenience.
(H1)  for any
for any  and there exist
and there exist  and
and  such that
such that

uniformly for  , and
, and

(H2) For any  and countable bounded set
and countable bounded set  , there exist
, there exist  such that
such that

with

where  .
.
(H3)  imply
imply

In what follows, we write  and
and  . Evidently,
. Evidently,  , and
, and  are closed convex sets in
are closed convex sets in  and
and  , respectively.
, respectively.
We will reduce BVP (1.2) to a system of integral equations in  . To this end, we first consider operator
. To this end, we first consider operator  defined by
defined by

where


Lemma 2.1.
If condition  is satisfied, then operator
is satisfied, then operator  defined by (2.12) is a continuous operator from
defined by (2.12) is a continuous operator from  into
into  .
.
Proof.
Let


By virtue of condition  , there exists an
, there exists an  such that
such that

where

Hence

Let  , we have, by (2.19)
, we have, by (2.19)

which together with condition  implies the convergence of the infinite integral
implies the convergence of the infinite integral

Thus, we have

which together with (2.13) and  implies that
implies that

Therefore, by (2.15) and (2.20), we get

Differentiating (2.13), we obtain

Hence,

It follows from (2.24) and (2.25) that

So,  . On the other hand, it can be easily seen that
. On the other hand, it can be easily seen that

So,  . In the same way, we can easily get that
. In the same way, we can easily get that

where  Thus,
Thus,  maps
maps  into
into  and we get
and we get

where

Finally, we show that  is continuous. Let
is continuous. Let  . Then
. Then  is a bounded subset of
is a bounded subset of  . Thus, there exists
. Thus, there exists  such that
such that  for
for  and
and  . Similar to (2.24) and (2.26), it is easy to have
. Similar to (2.24) and (2.26), it is easy to have

It is clear,

and by (2.20),

It follows from (2.33) and (2.34) and the dominated convergence theorem that

It follows from (2.32) and (2.35) that  as
as  . By the same method, we have
. By the same method, we have  as
as  . Therefore, the continuity of
. Therefore, the continuity of  is proved.
is proved.
Lemma 2.2.
If condition  is satisfied, then
is satisfied, then  is a solution of BVP (1.2) if and only if
is a solution of BVP (1.2) if and only if  is a fixed point of operator
is a fixed point of operator  .
.
Proof.
Suppose that  is a solution of BVP (1.2). For
is a solution of BVP (1.2). For  integrating (1.2) from
integrating (1.2) from  to
to  , we have
, we have

Integrating (2.36) from 0 to  , we get
, we get


Thus, we obtain

which together with the boundary value conditions imply that


Substituting (2.40) and (2.41) into (2.37) and (2.38), respectively, we have

It follows from Lemma 2.1 that the integral  and the integral
and the integral  are convergent. Thus,
are convergent. Thus,  is a fixed point of operator
is a fixed point of operator  .
.
Conversely, if  is fixed point of operator
is fixed point of operator  , then direct differentiation gives the proof.
, then direct differentiation gives the proof.
Lemma 2.3.
Let  be satisfied,
be satisfied,  is a bounded set. Then
is a bounded set. Then  and
and  are equicontinuous on any finite subinterval of
are equicontinuous on any finite subinterval of  and for any
and for any  there exists
there exists  such that
such that

uniformly with respect to  as
as 
Proof.
We only give the proof for operator  , the proof for operator
, the proof for operator  can be given in a similar way. By (2.13), we have
can be given in a similar way. By (2.13), we have

For  we obtain by (2.44)
we obtain by (2.44)

Then, it is easy to see by (2.45) and  that
that  is equicontinuous on any finite subinterval of
is equicontinuous on any finite subinterval of  .
.
Since  is bounded, there exists
is bounded, there exists  such that for any
such that for any  . By (2.25), we get
. By (2.25), we get

It follows from (2.46) and  and the absolute continuity of Lebesgue integral that
and the absolute continuity of Lebesgue integral that  is equicontinuous on any finite subinterval of
is equicontinuous on any finite subinterval of  .
.
In the following, we are in position to show that for any  there exists
there exists  such that
such that

uniformly with respect to  as
as 
Combining with (2.45), we need only to show that for any  there exists sufficiently large
there exists sufficiently large  such that
such that

for all  as
as  The rest part of the proof is very similar to Lemma
The rest part of the proof is very similar to Lemma  in [5], we omit the details.
in [5], we omit the details.
Lemma 2.4.
Let  be a bounded set in
be a bounded set in  . Assume that
. Assume that  holds. Then
holds. Then

Proof.
The proof is similar to that of Lemma  in [5], we omit it.
in [5], we omit it.
Mönch Fixed-Point Theorem. Let  be a closed convex set of
be a closed convex set of  and
and  Assume that the continuous operator
Assume that the continuous operator  has the following property:
has the following property:  countable,
countable,  is relatively compact. Then
is relatively compact. Then  has a fixed point in
has a fixed point in  .
.
Lemma 2.6.
If  is satisfied, then for
is satisfied, then for  imply that
imply that 
Proof.
It is easy to see that this lemma follows from (2.13), (2.25), and condition  . The proof is obvious.
. The proof is obvious.
Lemma 2.7 (see [16]).
Let  and
and  are bounded sets in
are bounded sets in  , then
, then

where  and
and  denote the Kuratowski measure of noncompactness in
denote the Kuratowski measure of noncompactness in  and
and  , respectively.
, respectively.
Lemma 2.8 (see [16]).
Let  be normal (fully regular) in
be normal (fully regular) in  ,
,  then
then  is normal (fully regular) in
is normal (fully regular) in  .
.
3. Main Results
Theorem 3.1.
If conditions  and
and  are satisfied, then BVP (1.2) has a positive solution
are satisfied, then BVP (1.2) has a positive solution  satisfying
satisfying  for
for 
Proof.
By Lemma 2.1, operator  defined by (2.13) is a continuous operator from
defined by (2.13) is a continuous operator from  into
into  , and, by Lemma 2.2, we need only to show that
, and, by Lemma 2.2, we need only to show that  has a fixed point
has a fixed point  in
in  . Choose
. Choose  and let
and let  . Obviously,
. Obviously,  is a bounded closed convex set in space
is a bounded closed convex set in space  . It is easy to see that
. It is easy to see that  is not empty since
is not empty since  . It follows from (2.27) and (3.6) that
. It follows from (2.27) and (3.6) that  implies
implies  , that is,
, that is,  maps
maps  into
into  . Let
. Let  satisfying
satisfying  for some
for some  . Then
. Then  We have, by (2.13) and (2.25),
We have, by (2.13) and (2.25),

By Lemma 2.4, we have

where  , and
, and  .
.
By (2.21), we know that the infinite integral  is convergent uniformly for
is convergent uniformly for  So, for any
So, for any  we can choose a sufficiently large
we can choose a sufficiently large  such that
such that

Then, by [1, Theorem  ], (2.44), (3.1), (3.3),
], (2.44), (3.1), (3.3),  , and Lemma 2.7, we obtain
, and Lemma 2.7, we obtain

It follows from (3.2) and (3.4) that

In the same way, we get

On the other hand,  . Then, (3.5), (3.6),
. Then, (3.5), (3.6),  , and Lemma 2.7 imply
, and Lemma 2.7 imply  that is,
that is,  is relatively compact in
is relatively compact in  Hence, the Mönch fixed point theorem guarantees that
Hence, the Mönch fixed point theorem guarantees that  has a fixed point
has a fixed point  in
in  . Thus, Theorem 3.1 is proved.
. Thus, Theorem 3.1 is proved.
Theorem 3.2.
Let cone  be normal and conditions
be normal and conditions  be satisfied. Then BVP (1.2) has a positive solution
be satisfied. Then BVP (1.2) has a positive solution  which is minimal in the sense that
which is minimal in the sense that  for any positive solution
for any positive solution  of BVP (1.2). Moreover,
of BVP (1.2). Moreover,  and there exists a monotone iterative sequence
and there exists a monotone iterative sequence  such that
such that  as
as  uniformly on
uniformly on  and
and  as
as  for any
for any  where
where




Proof.
From (3.7), one can see that  and
and

By (3.7) and (3.11), we have that  and
and

which imply that  . Similarly, we have
. Similarly, we have  . Thus,
. Thus,  . It follows from (2.13) and (3.9) that
. It follows from (2.13) and (3.9) that

By Lemma 2.1, we get  and
and

By Lemma 2.6 and (3.13), we have

It follows from (3.14), by induction, that

Let  Then,
Then,  is a bounded closed convex set in space
is a bounded closed convex set in space  and operator
and operator  maps
maps  into
into  . Clearly,
. Clearly,  is not empty since
is not empty since  Let
Let  Obviously,
Obviously,  and
and  Similar to above proof of Theorem 3.1, we can obtain
Similar to above proof of Theorem 3.1, we can obtain  that is,
that is,  is relatively compact in
is relatively compact in  So, there exists an
So, there exists an  and a subsequence
and a subsequence  such that
such that  converges to
converges to  uniformly on
uniformly on  Since that
Since that  is normal and
is normal and  is nondecreasing, it is easy to see that the entire sequence
is nondecreasing, it is easy to see that the entire sequence  converges to
converges to  uniformly on
uniformly on  Since
Since  and
and  are closed convex sets in space
are closed convex sets in space  , we have
, we have  It is clear,
It is clear,

By  and (3.16), we have
and (3.16), we have

Noticing (3.17) and (3.18) and taking limit as  in (3.9), we obtain
in (3.9), we obtain

In the same way, taking limit as  in (3.10), we get
in (3.10), we get

which together with (3.19) and Lemma 2.2 implies that  and
and  is a positive solution of BVP (1.2). Differentiating (3.9) twice, we get
is a positive solution of BVP (1.2). Differentiating (3.9) twice, we get

Hence, by (3.17), we obtain

Similarly, we have

Let  be any positive solution of BVP (1.2). By Lemma 2.2, we have
be any positive solution of BVP (1.2). By Lemma 2.2, we have  and
and  for
for  It is clear that
It is clear that  for any
for any  So, by Lemma 2.6, we have
So, by Lemma 2.6, we have  for any
for any  Assume that
Assume that  for
for  Then, it follows from Lemma 2.6 that
Then, it follows from Lemma 2.6 that  for
for  that is,
that is,  for
for  Hence, by induction, we get
Hence, by induction, we get

Now, taking limits in (3.24), we get  for
for  and the theorem is proved.
and the theorem is proved.
Theorem 3.3.
Let cone  be fully regular and conditions
be fully regular and conditions  and
and  be satisfied. Then the conclusion of Theorem 3.2 holds.
be satisfied. Then the conclusion of Theorem 3.2 holds.
Proof.
The proof is almost the same as that of Theorem 3.2. The only difference is that, instead of using condition  , the conclusion
, the conclusion  is implied directly by (3.15) and (3.16), the full regularity of
is implied directly by (3.15) and (3.16), the full regularity of  and Lemma 2.4.
and Lemma 2.4.
4. An Example
Consider the infinite system of scalar singular second order three-point boundary value problems:

Proposition 4.1.
Infinite system (4.1) has a minimal positive solution  satisfying
satisfying  for
for 
Proof.
Let  with the norm
with the norm  . Obviously,
. Obviously,  is a real Banach space. Choose
is a real Banach space. Choose  . It is easy to verify that
. It is easy to verify that  is a normal cone in
is a normal cone in  with normal constants 1. Now we consider infinite system (4.1), which can be regarded as a BVP of form (1.2) in
with normal constants 1. Now we consider infinite system (4.1), which can be regarded as a BVP of form (1.2) in  with
with  . In this situation,
. In this situation,  in which
in which

Let  . Then
. Then  for
for  . It is clear,
. It is clear,  for any
for any  . Notice that
. Notice that  for
for  , by (4.2), we get
, by (4.2), we get

which imply  is satisfied for
is satisfied for  and
and

Let  ,
, where
where




Let 
 be given, and
be given, and  be any sequence in
be any sequence in  , where
, where  . By (4.5), we have
. By (4.5), we have

So,  is bounded and by the diagonal method together with the method of constructing subsequence, we can choose a subsequence
is bounded and by the diagonal method together with the method of constructing subsequence, we can choose a subsequence  such that
such that

which implies by virtue of (4.9)

Hence  It is easy to see from (4.9)–(4.11) that
It is easy to see from (4.9)–(4.11) that

Thus, we have proved that  is relatively compact in
is relatively compact in 
For any  , we have by (4.6)
, we have by (4.6)

where  is between
is between  and
and  . By (4.13), we get
. By (4.13), we get

In the same way, we can prove that  is relatively compact in
is relatively compact in  , and we can also get
, and we can also get

Thus, by (4.14) and (4.15), it is easy to see that  holds for
holds for  . Thus, our conclusion follows from Theorem 3.1. This completes the proof.
. Thus, our conclusion follows from Theorem 3.1. This completes the proof.
References
Guo DJ, Lakshmikantham V, Liu XZ: Nonlinear Integral Equations in Abstract Spaces, Mathematics and Its Applications. Volume 373. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:viii+341.
Deimling K: Ordinary Differential Equations in Banach Spaces, Lecture Notes in Mathematics. Volume 596. Springer, Berlin, Germany; 1977:vi+137.
Lakshmikantham V, Leela S: Nonlinear Differential Equations in Abstract Spaces, International Series in Nonlinear Mathematics: Theory, Methods and Applications. Volume 2. Pergamon Press, Oxford, UK; 1981:x+258.
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Liu Y: Boundary value problems for second order differential equations on unbounded domains in a Banach space. Applied Mathematics and Computation 2003, 135(2-3):569-583. 10.1016/S0096-3003(02)00070-X
Gupta CP: Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. Journal of Mathematical Analysis and Applications 1992, 168(2):540-551. 10.1016/0022-247X(92)90179-H
Feng W, Webb JRL:Solvability of
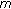 -point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997, 212(2):467-480. 10.1006/jmaa.1997.5520
-point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997, 212(2):467-480. 10.1006/jmaa.1997.5520Sun JX, Xu X, O'Regan D:Nodal solutions for
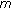 -point boundary value problems using bifurcation methods. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3034-3046. 10.1016/j.na.2007.02.043
-point boundary value problems using bifurcation methods. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3034-3046. 10.1016/j.na.2007.02.043Xu X:Positive solutions for singular
 -point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004, 291(1):352-367. 10.1016/j.jmaa.2003.11.009
-point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004, 291(1):352-367. 10.1016/j.jmaa.2003.11.009Ma R, Castaneda N:Existence of solutions of nonlinear
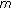 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556-567. 10.1006/jmaa.2000.7320Zhao J, Liu Z, Liu L: The existence of solutions of infinite boundary value problems for first-order impulsive differential systems in Banach spaces. Journal of Computational and Applied Mathematics 2008, 222(2):524-530. 10.1016/j.cam.2007.11.020
Zhang G, Sun JX:Positive solutions of
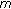 -point boundary value problems. Journal of Mathematical Analysis and Applications 2004, 291(2):406-418. 10.1016/j.jmaa.2003.11.034
-point boundary value problems. Journal of Mathematical Analysis and Applications 2004, 291(2):406-418. 10.1016/j.jmaa.2003.11.034Zhao Y-L, Chen H-B:Existence of multiple positive solutions for
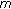 -point boundary value problems in Banach spaces. Journal of Computational and Applied Mathematics 2008, 215(1):79-90. 10.1016/j.cam.2007.03.025
-point boundary value problems in Banach spaces. Journal of Computational and Applied Mathematics 2008, 215(1):79-90. 10.1016/j.cam.2007.03.025Liu B: Positive solutions of a nonlinear four-point boundary value problems in Banach spaces. Journal of Mathematical Analysis and Applications 2005, 305(1):253-276. 10.1016/j.jmaa.2004.11.037
Guo DJ:Existence of positive solutions for
 th-order nonlinear impulsive singular integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(9):2727-2740. 10.1016/j.na.2007.02.019
th-order nonlinear impulsive singular integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(9):2727-2740. 10.1016/j.na.2007.02.019Guo DJ, Lakshmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Analysis: Theory, Methods & Applications 1987, 11(5):623-632. 10.1016/0362-546X(87)90077-0
Acknowledgment
The project is supported financially by the National Natural Science Foundation of China (10671167) and the Natural Science Foundation of Liaocheng University (31805).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, X. Positive Solutions of Singular Multipoint Boundary Value Problems for Systems of Nonlinear Second-Order Differential Equations on Infinite Intervals in Banach Spaces. Bound Value Probl 2009, 978605 (2009). https://doi.org/10.1155/2009/978605
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/978605
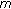 -point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997, 212(2):467-480. 10.1006/jmaa.1997.5520
-point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997, 212(2):467-480. 10.1006/jmaa.1997.5520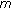 -point boundary value problems using bifurcation methods. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3034-3046. 10.1016/j.na.2007.02.043
-point boundary value problems using bifurcation methods. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(10):3034-3046. 10.1016/j.na.2007.02.043 -point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004, 291(1):352-367. 10.1016/j.jmaa.2003.11.009
-point boundary value problems with positive parameter. Journal of Mathematical Analysis and Applications 2004, 291(1):352-367. 10.1016/j.jmaa.2003.11.009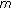 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001, 256(2):556-567. 10.1006/jmaa.2000.7320 -point boundary value problems. Journal of Mathematical Analysis and Applications 2004, 291(2):406-418. 10.1016/j.jmaa.2003.11.034
-point boundary value problems. Journal of Mathematical Analysis and Applications 2004, 291(2):406-418. 10.1016/j.jmaa.2003.11.034 -point boundary value problems in Banach spaces. Journal of Computational and Applied Mathematics 2008, 215(1):79-90. 10.1016/j.cam.2007.03.025
-point boundary value problems in Banach spaces. Journal of Computational and Applied Mathematics 2008, 215(1):79-90. 10.1016/j.cam.2007.03.025 th-order nonlinear impulsive singular integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(9):2727-2740. 10.1016/j.na.2007.02.019
th-order nonlinear impulsive singular integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(9):2727-2740. 10.1016/j.na.2007.02.019