- Research Article
- Open access
- Published:
Sign-Changing and Extremal Constant-Sign Solutions of Nonlinear Elliptic Neumann Boundary Value Problems
Boundary Value Problems volume 2010, Article number: 139126 (2010)
Abstract
Our aim is the study of a class of nonlinear elliptic problems under Neumann conditions involving the  -Laplacian. We prove the existence of at least three nontrivial solutions, which means that we get two extremal constant-sign solutions and one sign-changing solution by using truncation techniques and comparison principles for nonlinear elliptic differential inequalities. We also apply the properties of the Fu
-Laplacian. We prove the existence of at least three nontrivial solutions, which means that we get two extremal constant-sign solutions and one sign-changing solution by using truncation techniques and comparison principles for nonlinear elliptic differential inequalities. We also apply the properties of the Fu ik spectrum of the
ik spectrum of the  -Laplacian and, in particular, we make use of variational and topological tools, for example, critical point theory, Mountain-Pass Theorem, and the Second Deformation Lemma.
-Laplacian and, in particular, we make use of variational and topological tools, for example, critical point theory, Mountain-Pass Theorem, and the Second Deformation Lemma.
1. Introduction
Let  be a bounded domain with Lipschitz boundary
be a bounded domain with Lipschitz boundary  . We consider the following nonlinear elliptic boundary value problem. Find
. We consider the following nonlinear elliptic boundary value problem. Find  and constants
and constants  such that
such that

where  is the negative
is the negative  -Laplacian,
-Laplacian,  denotes the outer normal derivative of
denotes the outer normal derivative of  , and
, and  as well as
as well as  are the positive and negative parts of
are the positive and negative parts of  , respectively. The nonlinearities
, respectively. The nonlinearities  and
and  are some Carathéodory functions which are bounded on bounded sets. For reasons of simplification, we drop the notation for the trace operator
are some Carathéodory functions which are bounded on bounded sets. For reasons of simplification, we drop the notation for the trace operator  which is used on the functions defined on the boundary
which is used on the functions defined on the boundary  .
.
The motivation of our study is a recent paper of the author in [1] in which problem (1.1) was treated in case  . We extend this approach and prove the existence of multiple solutions for the more general problem (1.1). To be precise, the existence of a smallest positive solution, a greatest negative solution, as well as a sign-changing solution of problem (1.1) is proved by using variational and topological tools, for example, critical point theory, Mountain-Pass Theorem, and the Second Deformation Lemma. Additionally, the Fu
. We extend this approach and prove the existence of multiple solutions for the more general problem (1.1). To be precise, the existence of a smallest positive solution, a greatest negative solution, as well as a sign-changing solution of problem (1.1) is proved by using variational and topological tools, for example, critical point theory, Mountain-Pass Theorem, and the Second Deformation Lemma. Additionally, the Fu ik spectrum for the
ik spectrum for the  -Laplacian takes an important part in our treatments.
-Laplacian takes an important part in our treatments.
Neumann boundary value problems in the form of (1.1) arise in different areas of pure and applied mathematics, for example, in the theory of quasiregular and quasiconformal mappings in Riemannian manifolds with boundary (see [2, 3]), in the study of optimal constants for the Sobolev trace embedding (see [4–7]), or at non-Newtonian fluids, flow through porus media, nonlinear elasticity, reaction diffusion problems, glaciology, and so on (see [8–11]).
The existence of multiple solutions for Neumann problems like those in the form of (1.1) has been studied by a number of authors, such as, for example, the authors of [12–15], and homogeneous Neumann boundary value problems were considered in [16, 17] and [15], respectively. Analogous results for the Dirichlet problem have been recently obtained in [18–21]. Further references can also be found in the bibliography of [1].
In our consideration, the nonlinearities  and
and  only need to be Carathéodory functions which are bounded on bounded sets whereby their growth does not need to be necessarily polynomial. The novelty of our paper is the fact that we do not need differentiability, polynomial growth, or some integral conditions on the mappings
only need to be Carathéodory functions which are bounded on bounded sets whereby their growth does not need to be necessarily polynomial. The novelty of our paper is the fact that we do not need differentiability, polynomial growth, or some integral conditions on the mappings  and
and  .
.
First, we have to make an analysis of the associated spectrum of (1.1). The Fu ik spectrum for the
ik spectrum for the  -Laplacian with a nonlinear boundary condition is defined as the set
-Laplacian with a nonlinear boundary condition is defined as the set  of
of  such that
such that

has a nontrivial solution. In view of the identity

we see at once that for  problem (1.2) reduces to the Steklov eigenvalue problem
problem (1.2) reduces to the Steklov eigenvalue problem

We say that  is an eigenvalue if (1.4) has nontrivial solutions. The first eigenvalue
is an eigenvalue if (1.4) has nontrivial solutions. The first eigenvalue  is isolated and simple and has a first eigenfunction
is isolated and simple and has a first eigenfunction  which is strictly positive in
which is strictly positive in  (see [22]). Furthermore, one can show that
(see [22]). Furthermore, one can show that  belongs to
belongs to  (cf., [23, Lemma
(cf., [23, Lemma  and Theorem
and Theorem  ] or [24, Theorem
] or [24, Theorem  ]), and along with the results of Lieberman in [25, Theorem
]), and along with the results of Lieberman in [25, Theorem  ] it holds that
] it holds that  . This fact combined with
. This fact combined with  in
in  yields
yields  , where
, where  denotes the interior of the positive cone
denotes the interior of the positive cone  in the Banach space
in the Banach space  , given by
, given by

Let us recall some properties of the Fu ik spectrum. If
ik spectrum. If  is an eigenvalue of (1.4), then the point
is an eigenvalue of (1.4), then the point  belongs to
belongs to  . Since the first eigenfunction of (1.4) is positive,
. Since the first eigenfunction of (1.4) is positive,  clearly contains the two lines
clearly contains the two lines  and
and  . A first nontrivial curve
. A first nontrivial curve  in
in  through
through  was constructed and variationally characterized by a mountain-pass procedure by Martínez and Rossi [26]. This yields the existence of a continuous path in
was constructed and variationally characterized by a mountain-pass procedure by Martínez and Rossi [26]. This yields the existence of a continuous path in  joining
joining  and
and  provided that
provided that  is above the curve
is above the curve  . The functional
. The functional  on
on  is given by
is given by

Due to the fact that  belongs to
belongs to  , there exists a variational characterization of the second eigenvalue of (1.4) meaning that
, there exists a variational characterization of the second eigenvalue of (1.4) meaning that  can be represented as
can be represented as

where

The proof of this result is given in [26].
An important part in our considerations takes the following Neumann boundary value problem defined by

where  is a constant. As pointed out in [1], there exists a unique solution
is a constant. As pointed out in [1], there exists a unique solution  of problem (1.9) which is required for the construction of sub- and supersolutions of problem (1.1).
of problem (1.9) which is required for the construction of sub- and supersolutions of problem (1.1).
2. Notations and Hypotheses
Now, we impose the following conditions on the nonlinearities  and
and  in problem (1.1). The maps
in problem (1.1). The maps  and
and  are Carathéodory functions, which means that they are measurable in the first argument and continuous in the second one. Furthermore, we suppose the following assumptions.
are Carathéodory functions, which means that they are measurable in the first argument and continuous in the second one. Furthermore, we suppose the following assumptions.
(H) (f1)

(f2)

(f3)  is bounded on bounded sets.
is bounded on bounded sets.
(f4) There exists  such that
such that

(H) (g1)

(g2)

(g3)  is bounded on bounded sets.
is bounded on bounded sets.
(g4)  satisfies the condition
satisfies the condition

for all pairs  in
in  , where
, where  is a positive constant and
is a positive constant and  .
.
(H) Let  be above the first nontrivial curve
be above the first nontrivial curve  of the Fu
of the Fu ik spectrum constructed in [26] (see Figure 1).
ik spectrum constructed in [26] (see Figure 1).
Note that (H2)(g4) implies that the function  fulfills a condition as in (H2)(g4), too. Moreover, we see at once that
fulfills a condition as in (H2)(g4), too. Moreover, we see at once that  is a trivial solution of problem (1.1) because of the conditions (H1)(f1) and (H2)(g1), which guarantees that
is a trivial solution of problem (1.1) because of the conditions (H1)(f1) and (H2)(g1), which guarantees that  . It should be noted that hypothesis (H3) includes that
. It should be noted that hypothesis (H3) includes that  (see [26] or Figure 1).
(see [26] or Figure 1).
Example 2.1.
Let the functions  and
and  be given by
be given by

Then all conditions in (H1)(f1)–(f4) and (H2)(g1)–(g4) are fulfilled.
Definition 2.2.
A function  is called a weak solution of (1.1) if the following holds:
is called a weak solution of (1.1) if the following holds:

Definition 2.3.
A function  is called a subsolution of (1.1) if the following holds:
is called a subsolution of (1.1) if the following holds:

Definition 2.4.
A function  is called a supersolution of (1.1) if the following holds:
is called a supersolution of (1.1) if the following holds:

We recall that  denotes all nonnegative functions of
denotes all nonnegative functions of  . Furthermore, for functions
. Furthermore, for functions  satisfying
satisfying  , we have the relation
, we have the relation  , where
, where  stands for the well-known trace operator.
stands for the well-known trace operator.
3. Extremal Constant-Sign Solutions
For the rest of the paper we denote by  the first eigenfunction of the Steklov eigenvalue problem (1.4) corresponding to its first eigenvalue
the first eigenfunction of the Steklov eigenvalue problem (1.4) corresponding to its first eigenvalue  . Furthermore, the function
. Furthermore, the function  stands for the unique solution of the auxiliary Neumann boundary value problem defined in (1.9). Our first lemma reads as follows.
stands for the unique solution of the auxiliary Neumann boundary value problem defined in (1.9). Our first lemma reads as follows.
Lemma 3.1.
Let conditions (H1)-(H2) be satisfied and let  . Then there exist constants
. Then there exist constants  such that
such that  and
and  are a positive supersolution and a negative subsolution, respectively, of problem (1.1).
are a positive supersolution and a negative subsolution, respectively, of problem (1.1).
Proof.
Setting  with a positive constant
with a positive constant  to be specified and considering the auxiliary problem (1.9), we obtain
to be specified and considering the auxiliary problem (1.9), we obtain

In order to satisfy Definition 2.4 for  , we have to show that the following inequality holds true meaning:
, we have to show that the following inequality holds true meaning:

where  with
with  . Condition (H1)(f2) implies the existence of
. Condition (H1)(f2) implies the existence of  such that
such that

and due to (H1)(f3), we have

Hence, we get

Because of hypothesis (H2)(g2), there exists  such that
such that

and thanks to condition (H2)(g3), we find a constant  such that
such that

Finally, we have

Using the inequality in (3.5) to the first integral in (3.2) yields

which proves its nonnegativity if  . Applying (3.8) to the second integral in (3.2) ensures that
. Applying (3.8) to the second integral in (3.2) ensures that

We take  to verify that both integrals in (3.2) are nonnegative. Hence, the function
to verify that both integrals in (3.2) are nonnegative. Hence, the function  is in fact a positive supersolution of problem (1.1). In a similar way one proves that
is in fact a positive supersolution of problem (1.1). In a similar way one proves that  is a negative subsolution, where we apply the following estimates:
is a negative subsolution, where we apply the following estimates:

This completes the proof.
The next two lemmas show that constant multipliers of  may be sub- and supersolution of (1.1). More precisely, we have the following result.
may be sub- and supersolution of (1.1). More precisely, we have the following result.
Lemma 3.2.
Assume that (H1)-(H2) are satisfied. If  , then for
, then for  sufficiently small and any
sufficiently small and any  the function
the function  is a positive subsolution of problem (1.1).
is a positive subsolution of problem (1.1).
Proof.
The Steklov eigenvalue problem (1.4) implies for all 

Definition 2.3 is satisfied for  provided that the inequality
provided that the inequality

is valid for all  . With regard to hypothesis (H1)(f4), we obtain, for
. With regard to hypothesis (H1)(f4), we obtain, for  ,
,

where  denotes the usual supremum norm. Thanks to condition (H2)(g1), there exists a number
denotes the usual supremum norm. Thanks to condition (H2)(g1), there exists a number  such that
such that

In case  we get
we get

Selecting  guarantees that
guarantees that  is a positive subsolution.
is a positive subsolution.
The following lemma on the existence of a negative supersolution can be proved in a similar way.
Lemma 3.3.
Assume that (H1)-(H2) are satisfied. If  , then for
, then for  sufficiently small and any
sufficiently small and any  the function
the function  is a negative supersolution of problem (1.1).
is a negative supersolution of problem (1.1).
Concerning Lemmas 3.1–3.3, we obtain a positive pair  and a negative pair
and a negative pair  of sub- and supersolutions of problem (1.1) provided that
of sub- and supersolutions of problem (1.1) provided that  is sufficiently small.
is sufficiently small.
In the next step we are going to prove the regularity of solutions of problem (1.1) belonging to the order intervals  and
and  , respectively. We also point out that
, respectively. We also point out that  is both a subsolution and a supersolution because of the hypotheses (H1)(f1) and (H2)(g1).
is both a subsolution and a supersolution because of the hypotheses (H1)(f1) and (H2)(g1).
Lemma 3.4.
Assume (H1)-(H2) and let  . If
. If  (resp.,
(resp.,  ) is a solution of problem (1.1) satisfying
) is a solution of problem (1.1) satisfying  in
in  , then it holds that
, then it holds that  (resp.,
(resp.,  ).
).
Proof.
We just show the first case; the other case acts in the same way. Let  be a solution of (1.1) satisfying
be a solution of (1.1) satisfying  . We directly obtain the
. We directly obtain the  -boundedness, and, hence, the regularity results of Lieberman in [25, Theorem
-boundedness, and, hence, the regularity results of Lieberman in [25, Theorem  ] imply that
] imply that  with
with  . Due to assumptions (H1)(f1), (H1)(f3), (H2)(g1), and (H2)(g3), we obtain the existence of constants
. Due to assumptions (H1)(f1), (H1)(f3), (H2)(g1), and (H2)(g3), we obtain the existence of constants  satisfying
satisfying

Applying (3.17) to (1.1) provides

where  is a positive constant. We set
is a positive constant. We set  for all
for all  and use Vázquez's strong maximum principle (cf., [27]) which is possible because
and use Vázquez's strong maximum principle (cf., [27]) which is possible because  . Hence, it holds that
. Hence, it holds that  in
in  . Finally, we suppose the existence of
. Finally, we suppose the existence of  satisfying
satisfying  . Applying again the maximum principle yields
. Applying again the maximum principle yields  . However, because of
. However, because of  in combination with the Neumann condition in (1.1), we get
in combination with the Neumann condition in (1.1), we get  . This is a contradiction and, hence,
. This is a contradiction and, hence,  in
in  , which proves that
, which proves that  .
.
The main result in this section about the existence of extremal constant-sign solutions is given in the following theorem.
Theorem 3.5.
Assume (H1)-(H2). For every  and
and  , there exists a smallest positive solution
, there exists a smallest positive solution  of (1.1) in the order interval
of (1.1) in the order interval  with the constant
with the constant  as in Lemma 3.1. For every
as in Lemma 3.1. For every  and
and  there exists a greatest solution
there exists a greatest solution  in the order interval
in the order interval  with the constant
with the constant  as in Lemma 3.1.
as in Lemma 3.1.
Proof.
Let  . Lemmas 3.1 and 3.2 guarantee that
. Lemmas 3.1 and 3.2 guarantee that  is a subsolution of problem (1.1) and
is a subsolution of problem (1.1) and  is a supersolution of problem (1.1). Moreover, we choose
is a supersolution of problem (1.1). Moreover, we choose  sufficiently small such that
sufficiently small such that  . Applying the method of sub- and supersolution (see [28]) corresponding to the order interval
. Applying the method of sub- and supersolution (see [28]) corresponding to the order interval  provides the existence of a smallest positive solution
provides the existence of a smallest positive solution  of problem (1.1) fulfilling
of problem (1.1) fulfilling  . In view of Lemma 3.4, we have
. In view of Lemma 3.4, we have  . Hence, for every positive integer
. Hence, for every positive integer  sufficiently large, there exists a smallest solution
sufficiently large, there exists a smallest solution  of problem (1.1) in the order interval
of problem (1.1) in the order interval  . We obtain
. We obtain

with some function  satisfying
satisfying  .
.
Claim 1.
 is a solution of problem (1.1).
is a solution of problem (1.1).
As  and
and  , we obtain the boundedness of
, we obtain the boundedness of  in
in  and
and  , respectively. Definition 2.2 holds, in particular, for
, respectively. Definition 2.2 holds, in particular, for  and
and  which results in
which results in

with some positive constants  independent of
independent of  . Consequently,
. Consequently,  is bounded in
is bounded in  and due to the reflexivity of
and due to the reflexivity of  we obtain the existence of a weakly convergent subsequence of
we obtain the existence of a weakly convergent subsequence of  . Because of the compact embedding
. Because of the compact embedding  , the monotony of
, the monotony of  , and the compactness of the trace operator
, and the compactness of the trace operator  , we get for the entire sequence
, we get for the entire sequence 

Since  solves problem (1.1), one obtains, for all
solves problem (1.1), one obtains, for all  ,
,

Setting  in (3.22) results in
in (3.22) results in

Using (3.21) and the hypotheses (H1)(f3) as well as (H2)(g3) yields

which provides, by the  -property of
-property of  on
on  along with (3.21),
along with (3.21),

The uniform boundedness of the sequence  in conjunction with the strong convergence in (3.25) and conditions (H1)(f3) as well as (H2)(g3) admit us to pass to the limit in (3.22). This shows that
in conjunction with the strong convergence in (3.25) and conditions (H1)(f3) as well as (H2)(g3) admit us to pass to the limit in (3.22). This shows that  is a solution of problem (1.1).
is a solution of problem (1.1).
Claim 2.
One has  .
.
In order to apply Lemma 3.4, we have to prove that  . Let us assume that this assertion is not valid meaning that
. Let us assume that this assertion is not valid meaning that  . From (3.19) it follows that
. From (3.19) it follows that

We set

It is clear that the sequence  is bounded in
is bounded in  which ensures the existence of a weakly convergent subsequence of
which ensures the existence of a weakly convergent subsequence of  , denoted again by
, denoted again by  , such that
, such that

with some function  belonging to
belonging to  . In addition, we may suppose that there are functions
. In addition, we may suppose that there are functions  such that
such that

With the aid of (3.22), we obtain for  the following variational equation:
the following variational equation:

We select  in the last equality to get
in the last equality to get

Making use of (3.17) in combination with (3.29) results in

and, respectively,

We see at once that the right-hand sides of (3.32) and (3.33) belong to  and
and  , respectively, which allows us to apply Lebesgue's dominated convergence theorem. This fact and the convergence properties in (3.28) show that
, respectively, which allows us to apply Lebesgue's dominated convergence theorem. This fact and the convergence properties in (3.28) show that

From (3.28), (3.31), and (3.34) we infer that

and the  -property of
-property of  corresponding to
corresponding to  implies that
implies that

Remark that  , which means that
, which means that  . Applying (3.26) and (3.36) along with conditions (H1)(f1), (H2)(g1) to (3.30) provides
. Applying (3.26) and (3.36) along with conditions (H1)(f1), (H2)(g1) to (3.30) provides

The equation above is the weak formulation of the Steklov eigenvalue problem in (1.4) where  is the eigenfunction with respect to the eigenvalue
is the eigenfunction with respect to the eigenvalue  . As
. As  is nonnegative in
is nonnegative in  , we get a contradiction to the results of Martínez and Rossi in [22, Lemma
, we get a contradiction to the results of Martínez and Rossi in [22, Lemma  ] because
] because  must change sign on
must change sign on  . Hence,
. Hence,  . Applying Lemma 3.4 yields
. Applying Lemma 3.4 yields  .
.
Claim 3.
 is the smallest positive solution of (1.1) in
is the smallest positive solution of (1.1) in  .
.
Let  be a positive solution of (1.1) satisfying
be a positive solution of (1.1) satisfying  . Lemma 3.4 immediately implies that
. Lemma 3.4 immediately implies that  . Then there exists an integer
. Then there exists an integer  sufficiently large such that
sufficiently large such that  . However, we already know that
. However, we already know that  is the smallest solution of (1.1) in
is the smallest solution of (1.1) in  which yields
which yields  . Passing to the limit proves that
. Passing to the limit proves that  . Hence,
. Hence,  must be the smallest positive solution of (1.1). The existence of the greatest negative solution of (1.1) within
must be the smallest positive solution of (1.1). The existence of the greatest negative solution of (1.1) within  can be proved similarly. This completes the proof of the theorem.
can be proved similarly. This completes the proof of the theorem.
4. Variational Characterization of Extremal Solutions
Theorem 3.5 ensures the existence of extremal positive and negative solutions of (1.1) for all  and
and  denoted by
denoted by  and
and  , respectively. Now, we introduce truncation functions
, respectively. Now, we introduce truncation functions  and
and  as follows:
as follows:

For  the truncation operators on
the truncation operators on  apply to the corresponding traces
apply to the corresponding traces  . We just write for simplification
. We just write for simplification  without
without  . Furthermore, the truncation operators are continuous, uniformly bounded, and Lipschitz continuous with respect to the second argument. By means of these truncations, we define the following associated functionals given by
. Furthermore, the truncation operators are continuous, uniformly bounded, and Lipschitz continuous with respect to the second argument. By means of these truncations, we define the following associated functionals given by

which are well defined and belong to  . Due to the truncations, one can easily show that these functionals are coercive and weakly lower semicontinuous, which implies that their global minimizers exist. Moreover, they also satisfy the Palais-Smale condition.
. Due to the truncations, one can easily show that these functionals are coercive and weakly lower semicontinuous, which implies that their global minimizers exist. Moreover, they also satisfy the Palais-Smale condition.
Lemma 4.1.
Let  and
and  be the extremal constant-sign solutions of (1.1). Then the following hold.
be the extremal constant-sign solutions of (1.1). Then the following hold.
(i) A critical point  of
of  is a nonnegative solution of (1.1) satisfying
is a nonnegative solution of (1.1) satisfying  .
.
(ii) A critical point  of
of  is a nonpositive solution of (1.1) satisfying
is a nonpositive solution of (1.1) satisfying  .
.
(iii) A critical point  of
of  is a solution of (1.1) satisfying
is a solution of (1.1) satisfying  .
.
Proof.
Let  be a critical point of
be a critical point of  meaning
meaning  . We have for all
. We have for all 

As  is a positive solution of (1.1), it satisfies
is a positive solution of (1.1), it satisfies

Subtracting (4.4) from (4.3) and setting  provide
provide

Based on the definition of the truncation operators, we see that the right-hand side of the equality above is equal to zero. On the other hand, the integrals on the left-hand side are strictly positive in case  which is a contradiction. Thus, we get
which is a contradiction. Thus, we get  and, hence,
and, hence,  . The proof for
. The proof for  acts in a similar way which shows that
acts in a similar way which shows that  , and
, and  , and therefore,
, and therefore,  is a solution of (1.1) satisfying
is a solution of (1.1) satisfying  . The statements in (i) and (ii) can be shown in the same way.
. The statements in (i) and (ii) can be shown in the same way.
An important tool in our considerations is the relation between local  -minimizers and local
-minimizers and local  -minimizers for
-minimizers for  -functionals. The fact is that every local
-functionals. The fact is that every local  -minimizer of
-minimizer of  is a local
is a local  -minimizer of
-minimizer of  which was proved in similar form in [1, Proposition
which was proved in similar form in [1, Proposition  ]. This result reads as follows.
]. This result reads as follows.
Proposition 4.2.
If  is a local
is a local  -minimizer of
-minimizer of  meaning that there exists
meaning that there exists  such that
such that

then  is a local minimizer of
is a local minimizer of  in
in  meaning that there exists
meaning that there exists  such that
such that

We also refer to a recent paper (see [29]) in which the proposition above was extended to the more general case of nonsmooth functionals. With the aid of Proposition 4.2, we can formulate the next lemma about the existence of local and global minimizers with respect to the functionals  , and
, and  .
.
Lemma 4.3.
Let  and
and  . Then the extremal positive solution
. Then the extremal positive solution  of (1.1) is the unique global minimizer of the functional
of (1.1) is the unique global minimizer of the functional  , and the extremal negative solution
, and the extremal negative solution  of (1.1) is the unique global minimizer of the functional
of (1.1) is the unique global minimizer of the functional  . In addition, both
. In addition, both  and
and  are local minimizers of the functional
are local minimizers of the functional  .
.
Proof.
As  is coercive and weakly sequentially lower semicontinuous, its global minimizer
is coercive and weakly sequentially lower semicontinuous, its global minimizer  exists meaning that
exists meaning that  is a critical point of
is a critical point of  . Concerning Lemma 4.1, we know that
. Concerning Lemma 4.1, we know that  is a nonnegative solution of (1.1) satisfying
is a nonnegative solution of (1.1) satisfying  . Due to condition (H2)(g1), there exists a number
. Due to condition (H2)(g1), there exists a number  such that
such that

Choosing  and applying assumption (H1)(f4), inequality (4.8) along with the Steklov eigenvalue problem in (1.4) implies that
and applying assumption (H1)(f4), inequality (4.8) along with the Steklov eigenvalue problem in (1.4) implies that

From the calculations above, we see at once that  , which means that
, which means that  . This allows us to apply Lemma 3.4 getting
. This allows us to apply Lemma 3.4 getting  . Since
. Since  is the smallest positive solution of (1.1) in
is the smallest positive solution of (1.1) in  fulfilling
fulfilling  , it must hold that
, it must hold that  , which proves that
, which proves that  is the unique global minimizer of
is the unique global minimizer of  . The same considerations show that
. The same considerations show that  is the unique global minimizer of
is the unique global minimizer of  . In order to complete the proof, we are going to show that
. In order to complete the proof, we are going to show that  and
and  are local minimizers of the functional
are local minimizers of the functional  as well. The extremal positive solution
as well. The extremal positive solution  belongs to
belongs to  , which means that there is a neighborhood
, which means that there is a neighborhood  of
of  in the space
in the space  satisfying
satisfying  . Therefore,
. Therefore,  on
on  proves that
proves that  is a local minimizer of
is a local minimizer of  on
on  . Applying Proposition 4.2 yields that
. Applying Proposition 4.2 yields that  is also a local
is also a local  -minimizer of
-minimizer of  . Similarly, we see that
. Similarly, we see that  is a local minimizer of
is a local minimizer of  , which completes the proof.
, which completes the proof.
Lemma 4.4.
The functional  has a global minimizer
has a global minimizer  which is a nontrivial solution of (1.1) satisfying
which is a nontrivial solution of (1.1) satisfying  .
.
Proof.
As we know, the functional  is coercive and weakly sequentially lower semicontinuous. Hence, it has a global minimizer
is coercive and weakly sequentially lower semicontinuous. Hence, it has a global minimizer  . More precisely,
. More precisely,  is a critical point of
is a critical point of  which is a solution of (1.1) satisfying
which is a solution of (1.1) satisfying  (see Lemma 4.1). The fact that
(see Lemma 4.1). The fact that  (see the proof of Lemma 4.3) proves that
(see the proof of Lemma 4.3) proves that  is nontrivial meaning that
is nontrivial meaning that  .
.
5. Existence of Sign-Changing Solutions
The main result in this section about the existence of a nontrivial solution of problem (1.1) reads as follows.
Theorem 5.1.
Under hypotheses (H1)–(H3), problem (1.1) has a nontrivial sign-changing solution  .
.
Proof.
In view of Lemma 4.4, the existence of a global minimizer  of
of  satisfying
satisfying  has been proved. This means that
has been proved. This means that  is a nontrivial solution of (1.1) belonging to
is a nontrivial solution of (1.1) belonging to  . If
. If  and
and  , then
, then  must be a sign-changing solution because
must be a sign-changing solution because  is the greatest negative solution and
is the greatest negative solution and  is the smallest positive solution of (1.1), which proves the theorem in this case. We still have to show the theorem in case that either
is the smallest positive solution of (1.1), which proves the theorem in this case. We still have to show the theorem in case that either  or
or  . Let us only consider the case
. Let us only consider the case  because the case
because the case  can be proved similarly. The function
can be proved similarly. The function  is a local minimizer of
is a local minimizer of  . Without loss of generality, we suppose that
. Without loss of generality, we suppose that  is a strict local minimizer; otherwise, we would obtain infinitely many critical points
is a strict local minimizer; otherwise, we would obtain infinitely many critical points  of
of  which are sign-changing solutions due to
which are sign-changing solutions due to  and the extremality of the solutions
and the extremality of the solutions  . Under these assumptions, there exists a
. Under these assumptions, there exists a  such that
such that

where  . Now, we may apply the Mountain-Pass Theorem to
. Now, we may apply the Mountain-Pass Theorem to  (cf., [30]) thanks to (5.1) along with the fact that
(cf., [30]) thanks to (5.1) along with the fact that  satisfies the Palais-Smale condition. This yields the existence of
satisfies the Palais-Smale condition. This yields the existence of  satisfying
satisfying  and
and

where

It is clear that (5.1) and (5.2) imply that  and
and  . Hence,
. Hence,  is a sign-changing solution provided that
is a sign-changing solution provided that  . We have to show that
. We have to show that  which is fulfilled if there exists a path
which is fulfilled if there exists a path  such that
such that

Let  , where
, where  , and
, and  be equipped with the topologies induced by
be equipped with the topologies induced by  and
and  , respectively. Furthermore, we set
, respectively. Furthermore, we set

Because of the results of Martínez and Rossi in [26], there exists a continuous path  satisfying
satisfying  provided that
provided that  is above the curve
is above the curve  of hypothesis (H3). Recall that the functional
of hypothesis (H3). Recall that the functional  is given by
is given by

This implies the existence of  such that
such that

It is well known that  is dense in
is dense in  , which implies the density of
, which implies the density of  in
in  . Thus, a continuous path
. Thus, a continuous path  exists such that
exists such that

The boundedness of the set  in
in  ensures the existence of
ensures the existence of  such that
such that

Theorem 3.5 yields that  . Thus, for every
. Thus, for every  and any bounded neighborhood
and any bounded neighborhood  of
of  in
in  there exist positive numbers
there exist positive numbers  and
and  satisfying
satisfying

for all  , for all
, for all  , and for all
, and for all  . Using (5.10) along with a compactness argument implies the existence of
. Using (5.10) along with a compactness argument implies the existence of  such that
such that

for all  , for all
, for all  , and for all
, and for all  . Representing
. Representing  in terms of
in terms of  , we obtain
, we obtain

In view of (5.11) we get for all  and all
and all 

Due to hypotheses (H1)(f1) and (H2)(g1), there exist positive constants  such that
such that

Choosing  such that
such that  and using (5.14) provide
and using (5.14) provide

Applying (5.15) to (5.13) yields

We have constructed a continuous path  joining
joining  and
and  . In order to construct continuous paths
. In order to construct continuous paths  connecting
connecting  and
and  , respectively,
, respectively,  and
and  , we first denote that
, we first denote that

It holds that  because
because  is a global minimizer of
is a global minimizer of  . By Lemma 4.1 the functional
. By Lemma 4.1 the functional  has no critical values in the interval
has no critical values in the interval  . The coercivity of
. The coercivity of  along with its property to satisfy the Palais-Smale condition allows us to apply the Second Deformation Lemma (see, e.g., [31, page 366]) to
along with its property to satisfy the Palais-Smale condition allows us to apply the Second Deformation Lemma (see, e.g., [31, page 366]) to  . This ensures the existence of a continuous mapping
. This ensures the existence of a continuous mapping  satisfying the following properties:
satisfying the following properties:
(i)  , for all
, for all  ,
,
(ii)  , for all
, for all  ,
,
(iii)  , for all
, for all  and for all
and for all  .
.
Next, we introduce the path  given by
given by  for all
for all  which is obviously continuous in
which is obviously continuous in  joining
joining  and
and  . Additionally, one has
. Additionally, one has

Similarly, the Second Deformation Lemma can be applied to the functional  . We get a continuous path
. We get a continuous path  connecting
connecting  and
and  such that
such that

In the end, we combine the curves  , and
, and  to obtain a continuous path
to obtain a continuous path  joining
joining  and
and  . Taking into account (5.16), (5.18), and (5.19), we get
. Taking into account (5.16), (5.18), and (5.19), we get  . This yields the existence of a nontrivial sign-changing solution
. This yields the existence of a nontrivial sign-changing solution  of problem (1.1) satisfying
of problem (1.1) satisfying  which completes the proof.
which completes the proof.
References
Winkert P: Constant-sign and sign-changing solutions for nonlinear elliptic equations with neumann boundary values. Advances in Differential Equations 2010,15(5-6):561-599.
Escobar JF: Uniqueness theorems on conformal deformation of metrics, Sobolev inequalities, and an eigenvalue estimate. Communications on Pure and Applied Mathematics 1990,43(7):857-883. 10.1002/cpa.3160430703
Tolksdorf P: Regularity for a more general class of quasilinear elliptic equations. Journal of Differential Equations 1984,51(1):126-150. 10.1016/0022-0396(84)90105-0
del Pino M, Flores C: Asymptotic behavior of best constants and extremals for trace embeddings in expanding domains. Communications in Partial Differential Equations 2001,26(11-12):2189-2210. 10.1081/PDE-100107818
Bonder JF, Lami Dozo E, Rossi JD: Symmetry properties for the extremals of the Sobolev trace embedding. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2004,21(6):795-805.
Bonder JF, Martínez S, Rossi JD: The behavior of the best Sobolev trace constant and extremals in thin domains. Journal of Differential Equations 2004,198(1):129-148. 10.1016/j.jde.2003.07.011
Bonder JF:Multiple solutions for the
 -Laplace equation with nonlinear boundary conditions. Electronic Journal of Differential Equations 2006, (37):-7.
-Laplace equation with nonlinear boundary conditions. Electronic Journal of Differential Equations 2006, (37):-7.Arcoya D, Diaz JI, Tello L: S-shaped bifurcation branch in a quasilinear multivalued model arising in climatology. Journal of Differential Equations 1998,150(1):215-225. 10.1006/jdeq.1998.3502
Atkinson C, El-Ali K: Some boundary value problems for the Bingham model. Journal of Differential Equations 1992,41(3):339-363.
Atkinson C, Champion CR:On some boundary value problems for the equation
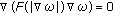 . Proceedings of the Royal Society A 1995,448(1933):269-279. 10.1098/rspa.1995.0016
. Proceedings of the Royal Society A 1995,448(1933):269-279. 10.1098/rspa.1995.0016Díaz JI: Nonlinear Partial Differential Equations and Free Boundaries. I. Elliptic Equations, Research Notes in Mathematics. Volume 106. Pitman, Boston, Mass, USA; 1985:vii+323.
Bonder JF: Multiple positive solutions for quasilinear elliptic problems with sign-changing nonlinearities. Abstract and Applied Analysis 2004,2004(12):1047-1055. 10.1155/S1085337504403078
Bonder JF, Rossi JD:Existence results for the
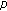 -Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001,263(1):195-223. 10.1006/jmaa.2001.7609
-Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001,263(1):195-223. 10.1006/jmaa.2001.7609Martínez SR, Rossi JD:Weak solutions for the
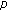 -Laplacian with a nonlinear boundary condition at resonance. Electronic Journal of Differential Equations 2003, (27):-14.
-Laplacian with a nonlinear boundary condition at resonance. Electronic Journal of Differential Equations 2003, (27):-14.Zhao J-H, Zhao P-H:Existence of infinitely many weak solutions for the
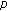 -Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1343-1355. 10.1016/j.na.2007.06.036
-Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1343-1355. 10.1016/j.na.2007.06.036Li C, Li S: Multiple solutions and sign-changing solutions of a class of nonlinear elliptic equations with Neumann boundary condition. Journal of Mathematical Analysis and Applications 2004,298(1):14-32. 10.1016/j.jmaa.2004.01.017
Wu X, Tan K-K: On existence and multiplicity of solutions of Neumann boundary value problems for quasi-linear elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(7):1334-1347. 10.1016/j.na.2005.10.010
Carl S, Motreanu D:Constant-sign and sign-changing solutions of a nonlinear eigenvalue problem involving the
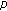 -Laplacian. Differential and Integral Equations 2007,20(3):309-324.
-Laplacian. Differential and Integral Equations 2007,20(3):309-324.Carl S, Motreanu D: Sign-changing and extremal constant-sign solutions of nonlinear elliptic problems with supercritical nonlinearities. Communications on Applied Nonlinear Analysis 2007,14(4):85-100.
Carl S, Motreanu D: Constant-sign and sign-changing solutions for nonlinear eigenvalue problems. Nonlinear Analysis: Theory, Methods & Applications 2008,68(9):2668-2676. 10.1016/j.na.2007.02.013
Carl S, Perera K:Sign-changing and multiple solutions for the
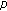 -Laplacian. Abstract and Applied Analysis 2002,7(12):613-625. 10.1155/S1085337502207010
-Laplacian. Abstract and Applied Analysis 2002,7(12):613-625. 10.1155/S1085337502207010Martínez SR, Rossi JD:Isolation and simplicity for the first eigenvalue of the
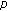 -Laplacian with a nonlinear boundary condition. Abstract and Applied Analysis 2002,7(5):287-293. 10.1155/S108533750200088X
-Laplacian with a nonlinear boundary condition. Abstract and Applied Analysis 2002,7(5):287-293. 10.1155/S108533750200088XLê A:Eigenvalue problems for the
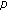 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057-1099. 10.1016/j.na.2005.05.056
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057-1099. 10.1016/j.na.2005.05.056Winkert P:
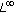 -estimates for nonlinear elliptic Neumann boundary value problems. Nonlinear Differential Equations and Applications 2010,17(3):289-302. 10.1007/s00030-009-0054-5
-estimates for nonlinear elliptic Neumann boundary value problems. Nonlinear Differential Equations and Applications 2010,17(3):289-302. 10.1007/s00030-009-0054-5Lieberman GM: Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 1988,12(11):1203-1219. 10.1016/0362-546X(88)90053-3
Martínez SR, Rossi JD:On the Fučik spectrum and a resonance problem for the
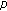 -Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(6):813-848.
-Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(6):813-848.Vázquez JL: A strong maximum principle for some quasilinear elliptic equations. Applied Mathematics and Optimization 1984,12(3):191-202.
Carl S: Existence and comparison results for noncoercive and nonmonotone multivalued elliptic problems. Nonlinear Analysis: Theory, Methods & Applications 2006,65(8):1532-1546. 10.1016/j.na.2005.10.028
Winkert P:Local
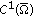 -minimizers versus local
-minimizers versus local 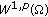 -minimizers of nonsmooth functionals. Nonlinear Analysis, Theory, Methods and Applications 2010,72(11):4298-4303. 10.1016/j.na.2010.02.006
-minimizers of nonsmooth functionals. Nonlinear Analysis, Theory, Methods and Applications 2010,72(11):4298-4303. 10.1016/j.na.2010.02.006Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. Conference Board of the Mathematical Sciences, Washington, DC, USA; 1986:viii+100.
Gasiński L, Papageorgiou NS: Nonsmooth Critical Point Theory and Nonlinear Boundary Value Problems, Series in Mathematical Analysis and Applications. Volume 8. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2005:xiv+775.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Winkert, P. Sign-Changing and Extremal Constant-Sign Solutions of Nonlinear Elliptic Neumann Boundary Value Problems. Bound Value Probl 2010, 139126 (2010). https://doi.org/10.1155/2010/139126
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/139126

 ik spectrum
ik spectrum
 -Laplace equation with nonlinear boundary conditions. Electronic Journal of Differential Equations 2006, (37):-7.
-Laplace equation with nonlinear boundary conditions. Electronic Journal of Differential Equations 2006, (37):-7. . Proceedings of the Royal Society A 1995,448(1933):269-279. 10.1098/rspa.1995.0016
. Proceedings of the Royal Society A 1995,448(1933):269-279. 10.1098/rspa.1995.0016 -Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001,263(1):195-223. 10.1006/jmaa.2001.7609
-Laplacian with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 2001,263(1):195-223. 10.1006/jmaa.2001.7609 -Laplacian with a nonlinear boundary condition at resonance. Electronic Journal of Differential Equations 2003, (27):-14.
-Laplacian with a nonlinear boundary condition at resonance. Electronic Journal of Differential Equations 2003, (27):-14. -Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1343-1355. 10.1016/j.na.2007.06.036
-Laplacian with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1343-1355. 10.1016/j.na.2007.06.036 -Laplacian. Differential and Integral Equations 2007,20(3):309-324.
-Laplacian. Differential and Integral Equations 2007,20(3):309-324. -Laplacian. Abstract and Applied Analysis 2002,7(12):613-625. 10.1155/S1085337502207010
-Laplacian. Abstract and Applied Analysis 2002,7(12):613-625. 10.1155/S1085337502207010 -Laplacian with a nonlinear boundary condition. Abstract and Applied Analysis 2002,7(5):287-293. 10.1155/S108533750200088X
-Laplacian with a nonlinear boundary condition. Abstract and Applied Analysis 2002,7(5):287-293. 10.1155/S108533750200088X -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057-1099. 10.1016/j.na.2005.05.056
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1057-1099. 10.1016/j.na.2005.05.056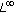 -estimates for nonlinear elliptic Neumann boundary value problems. Nonlinear Differential Equations and Applications 2010,17(3):289-302. 10.1007/s00030-009-0054-5
-estimates for nonlinear elliptic Neumann boundary value problems. Nonlinear Differential Equations and Applications 2010,17(3):289-302. 10.1007/s00030-009-0054-5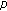 -Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(6):813-848.
-Laplacian with a nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(6):813-848.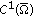 -minimizers versus local
-minimizers versus local 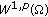 -minimizers of nonsmooth functionals. Nonlinear Analysis, Theory, Methods and Applications 2010,72(11):4298-4303. 10.1016/j.na.2010.02.006
-minimizers of nonsmooth functionals. Nonlinear Analysis, Theory, Methods and Applications 2010,72(11):4298-4303. 10.1016/j.na.2010.02.006