- Research Article
- Open access
- Published:
Approximate Controllability of a Reaction-Diffusion System with a Cross-Diffusion Matrix and Fractional Derivatives on Bounded Domains
Boundary Value Problems volume 2010, Article number: 281238 (2010)
Abstract
We study the following reaction-diffusion system with a cross-diffusion matrix and fractional derivatives  in
in  ,
,  in
in  ,
,  on
on  ,
,  ,
,  in
in  where
where  is a smooth bounded domain,
is a smooth bounded domain,  , the diffusion matrix
, the diffusion matrix  has semisimple and positive eigenvalues
has semisimple and positive eigenvalues  ,
,  ,
,  is an open nonempty set, and
is an open nonempty set, and  is the characteristic function of
is the characteristic function of  . Specifically, we prove that under some conditions over the coefficients
. Specifically, we prove that under some conditions over the coefficients  , the semigroup generated by the linear operator of the system is exponentially stable, and under other conditions we prove that for all
, the semigroup generated by the linear operator of the system is exponentially stable, and under other conditions we prove that for all  the system is approximately controllable on
the system is approximately controllable on  .
.
1. Introduction
In this paper we prove controllability for the following reaction-diffusion system with cross diffusion matrix:

where  is an open nonempty set of
is an open nonempty set of  and
and  is the characteristic function of
is the characteristic function of  .
.
We assume the following assumptions.
(H1)  is a smooth bounded domain in
is a smooth bounded domain in  .
.
(H2) The diffusion matrix  has semisimple and positive eigenvalues
has semisimple and positive eigenvalues 
(H3)  are real constants,
are real constants,  are real constants belonging to the interval
are real constants belonging to the interval 
(H4) 
(H5) The distributed controls  .
.
Specifically, we prove the following statements.
(i) If  and
and  , where
, where  is the first eigenvalue of
is the first eigenvalue of  with Dirichlet condition, or if
with Dirichlet condition, or if  , and
, and  then, under the hypotheses (H1)–(H3), the semigroup generated by the linear operator of the system is exponentially stable.
then, under the hypotheses (H1)–(H3), the semigroup generated by the linear operator of the system is exponentially stable.
(ii) If  and under the hypotheses (H1)–(H5), then, for all
and under the hypotheses (H1)–(H5), then, for all  and all open nonempty subset
and all open nonempty subset  of
of  the system is approximately controllable on
the system is approximately controllable on 
This paper has been motivated by the work done in [1] and the work done by H. Larez and H. Leiva in [2]. In the work [1], the auther studies the asymptotic behavior of the solution of the system

supplemeted with the initial conditions

The author proved that in the Banach space  where
where  is the space of bounded uniformly continuous real valued functions on
is the space of bounded uniformly continuous real valued functions on  , if
, if  and
and  are locally Lipshitz and under some conditions over the coefficients
are locally Lipshitz and under some conditions over the coefficients  , and if
, and if  then
then  for all
for all  Moreover,
Moreover,  and
and  satisfy the system of ordinary differential equations
satisfy the system of ordinary differential equations

with the initial data

The same result holds for 
In the work done in [2], the authers studied the system (1.1) with  , and
, and  They proved that if the diffusion matrix
They proved that if the diffusion matrix  has semi-simple and positive eigenvalues
has semi-simple and positive eigenvalues  ,
,  then if
then if  (
( is the first eigenvalue of
is the first eigenvalue of  ), the system is approximately controllable on
), the system is approximately controllable on  for all open nonempty subset
for all open nonempty subset  of
of 
2. Notations and Preliminaries
In the following we denote by
 the set of
the set of  matrices with entries from
matrices with entries from  ,
,
 the set of all measurable functions
the set of all measurable functions  such that
such that  ,
,
 the set of all the functions
the set of all the functions  that have generalized derivatives
that have generalized derivatives  for all
for all  ,
,
 the closure of the set
the closure of the set  in the Hilbert space
in the Hilbert space  ,
,
 the set of all the functions
the set of all the functions  that have generalized derivatives
that have generalized derivatives  for all
for all  .
.
We will use the following results.
Theorem 2.1 (cf. [3]).
Let us consider the following classical boundary-eigenvalue problem for the laplacien:

where  is a nonempty bounded open set in
is a nonempty bounded open set in  and
and  .
.
This problem has a countable system of eigenvalues  and
and  as
as  .
.
(i) All the eigenvalues  have finite multiplicity
have finite multiplicity  equal to the dimension of the corresponding eigenspace
equal to the dimension of the corresponding eigenspace  .
.
(ii) Let  be a basis of the
be a basis of the  for every
for every  then the eigenvectors
then the eigenvectors  form a complete orthonormal system in the space
form a complete orthonormal system in the space  Hence for all
Hence for all  we have
we have  If we put
If we put  then we get
then we get  .
.
(iii) Also, the eigenfunctions  , where
, where  is the space of infinitely continuously differentiable functions on
is the space of infinitely continuously differentiable functions on  and compactly supported in
and compactly supported in  .
.
(iv) For all  we have
we have  .
.
(v) The operator  generates an analytic semigroup
generates an analytic semigroup  on
on  defined by
defined by

Definition 2.2.
Let  a real number, the operator
a real number, the operator  is defined by
is defined by

In particular, we obtain  and
and  . Since
. Since  form a complete orthonormal system in the space
form a complete orthonormal system in the space  then it is dense in
then it is dense in  , and hence
, and hence  is dense in
is dense in  .
.
Proposition 2.3 (cf. [4]).
Let  be a Hilbert separable space and
be a Hilbert separable space and  and
and  two families of bounded linear operators in
two families of bounded linear operators in  , with
, with  a family of complete orthogonal projections such that
a family of complete orthogonal projections such that 
Define the following family of linear operators  Then
Then
(a)  is a linear and bounded operator if
is a linear and bounded operator if  with
with  continiuous for
continiuous for 
(b) under the above condition (a),  is a strongly continiuous semigroup in the Hilbert space
is a strongly continiuous semigroup in the Hilbert space  whose infinitesimal generator
whose infinitesimal generator  is given by
is given by

Theorem 2.4 (cf. [5]).
Suppose  is connected,
is connected,  is a real function in
is a real function in  , and
, and  on a nonempty open subset of
on a nonempty open subset of  . Then
. Then  in
in  .
.
3. Abstract Formulation of the Problem
In this section we consider the following notations.
-
(i)
 is a Hilbert space with the inner product
is a Hilbert space with the inner product

 We define
We define

-
(iii)
Let
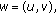 then we can define the linear operator
then we can define the linear operator

where

Therefore, for all 

If we put

then (3.3) can be written as

and we have for all 

Consequently, system (1.1) can be written as an abstract differential equation in the Hilbert space  in the following form:
in the following form:

where  and
and  is a bounded linear operator from
is a bounded linear operator from  into
into  .
.
4. Main Results
4.1. Generation of a  -Semigroup
-Semigroup
Theorem 4.1.
If  , then, under hypotheses (H1)–(H3), the linear operator
, then, under hypotheses (H1)–(H3), the linear operator  defined by (3.3) is the infinitesimal generator of strongly continuous semigroup
defined by (3.3) is the infinitesimal generator of strongly continuous semigroup  given by
given by

where


Moreover, if

then the  -semigoup
-semigoup  is exponentially stable, that is, there exist two positives constants
is exponentially stable, that is, there exist two positives constants  such that
such that

Proof.
In order to apply the Proposition 2.3, we observe that  can be written as follows:
can be written as follows:

where

Therefore,  and
and 
Now, we have to verify condition (a) of the Proposition 2.3. We shall suppose that  Then, there exists a set
Then, there exists a set  of complementary projections on
of complementary projections on  such that
such that

If  is the matrix passage from the canonical basis of
is the matrix passage from the canonical basis of  to the basis composed with the eigenvectors of
to the basis composed with the eigenvectors of  , then
, then

Hence,

We have also

From (4.10)-(4.11) into (4.7) we obtain

where

As  we get
we get

As  as
as  then this implies the existence of a positive number
then this implies the existence of a positive number  and a real number
and a real number  such that
such that  for every
for every  Therefore
Therefore  is a strongly continious semigroup
is a strongly continious semigroup  given by (4.1). We can even estimate the constants
given by (4.1). We can even estimate the constants  and
and  as follows.
as follows.
-
(i)
If
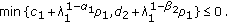 As
As  , then there exist constants
, then there exist constants 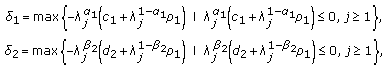 (4.15)
(4.15)
hence, if we put


we easily obtain

 If
If  . If we put
. If we put

then we find that

Therefore, the linear operator  generates a strongly continuous semigroup
generates a strongly continuous semigroup  on
on  given by expression (4.1).
given by expression (4.1).
Finally, if  we have already proved (4.20). Using (4.20) into (4.1) we get that the
we have already proved (4.20). Using (4.20) into (4.1) we get that the  -semigoup
-semigoup  is exponentially stable. The expression (4.5) is verfied with
is exponentially stable. The expression (4.5) is verfied with  and
and  is defined by (4.19).
is defined by (4.19).
Theorem 4.2.
If

then, under the hypotheses (H1)–(H3), the linear operator  defined by (3.3) is the infinitesimal generator of strongly continuous semigroup exponentially stable
defined by (3.3) is the infinitesimal generator of strongly continuous semigroup exponentially stable  defined by (4.1). Specially, there exist two positives constants
defined by (4.1). Specially, there exist two positives constants  such that
such that

To prove this result, we need the following lemma.
Lemma 4.3.
For every two real positives constants  and
and  , one has for every
, one has for every 

and for every 

Proof of Lemma 4.3.
It is easy to verify that for every  , for all
, for all  .
.
Let  and
and  , then we get
, then we get

Hence, we get (4.23).
Also, it is easy to verify that for every  , for all
, for all  . Let
. Let  and
and  , then we get
, then we get

Hence, from  (4.26) we get
(4.26) we get  for all
for all  and
and  , which gives (4.24).
, which gives (4.24).
With the same manner we can prove that for every  and every
and every  we have
we have

and consequently, for every two real positives constants  and
and  and every
and every  we have
we have

Now, we are ready to prove Theorem 4.2.
Proof of Theorem 4.2.
By applying Proposition 2.3 we start from formula (4.12) and we put

where

To estimate  we have in taking into account
we have in taking into account 

and applying the Lemma 4.3 we get
we get

for all  and
and  . But we have
. But we have  , for all
, for all  Then we get for every
Then we get for every  that
that

From (4.31)-(4.33) we get

where

and 
Applying Lemma 4.3 and taking into account (4.21) we get with the same manner that for every 

where

and or every 

where


From (4.34)-(4.40) into (4.12) we get

where  is defined by (4.17) and
is defined by (4.17) and

Using (4.41) into (4.1) we get that the  -semigoup
-semigoup  generated by
generated by  is exponentially stable. Expression (4.22) is verfied with
is exponentially stable. Expression (4.22) is verfied with  and
and  is defined by (4.42).
is defined by (4.42).
4.2. Approximate Controllability
Befor giving the definition of the approximate controllabiliy for the sytem (3.9), we have the following known result: for all  and
and  the initial value problem (3.9) admits a unique mild solution given by
the initial value problem (3.9) admits a unique mild solution given by

This solution is denoted by 
Definition 4.4.
System (3.9) is said to be approximately controllable at time  whenever the set
whenever the set  is densely embedded in
is densely embedded in  ; that is,
; that is,

The following criteria for approximate controllability can be found in [6].
Criteria 1.
System (3.9) is approximately controllable on  if and only if
if and only if

Now, we are ready to formulate the third main result of this work.
Theorem 4.5.
If the following condition

is satisfied; then, under hypotheses (H1)–(H5), for all  and all open subset
and all open subset  system (3.9) is approximately controllable on
system (3.9) is approximately controllable on  .
.
Proof.
The proof of this theorem relies on the Criteria 1 and the following lemma.
Lemma 4.6.
Let and
and  be sequences of real numbers such that
be sequences of real numbers such that  ,
,  and
and  , for all
, for all  , then for any
, then for any  one has
one has

Proof of Lemma 4.6.
By analyticity we get  and from this we get
and from this we get  . Under the assumptions of the lemma we get
. Under the assumptions of the lemma we get  as
as  and so
and so  If
If  , we divide
, we divide  by
by  and we pass
and we pass  we get
we get  . If
. If  we divide
we divide  by
by  and we pass
and we pass  and get
and get  . If
. If  , we divide
, we divide  by
by  and we pass
and we pass  and get
and get  But in this we case we can integrate under the symbol of sommation over the intervall
But in this we case we can integrate under the symbol of sommation over the intervall  and we get
and we get  . Hence
. Hence  . Continuing this way we see that
. Continuing this way we see that  for all
for all 
We are now ready to prove Theorem 4.5. For this purpose, we observe that

where  is the
is the  -semigroup generated by
-semigroup generated by  .
.
Without lose of generality, we suppose that  Hence
Hence

where 
Now, suppose for  that
that  , for all
, for all  Then
Then

If (4.46) is satisfied, then (4.50) take the form

Then, from lemma 4.6 we obtain that for  and all
and all 

Since  we get that all
we get that all 

On the other hand, from Theorem 2.4 we know that  are analytic functions, which implies the analticity of
are analytic functions, which implies the analticity of  and
and  Then we can conclude that for
Then we can conclude that for  and all
and all 

Hence  for all
for all  which implies that
which implies that  This completes the proof of Theorem 4.5.
This completes the proof of Theorem 4.5.
References
Badraoui S:Asymptotic behavior of solutions to a
 reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006,2006(61):1-13.
reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006,2006(61):1-13.Larez H, Leiva H:Interior controllability of a
 a reaction-diffusion system with cross diffusion matrix. to appear in Boundary Value Problems
a reaction-diffusion system with cross diffusion matrix. to appear in Boundary Value ProblemsZeidler E: Applied Functional Analysis, Applied Mathematical Sciences. Volume 109. Springer, New York, NY, USA; 1995:xvi+404.
Leiva H:A lemma on
 -semigroups and applications. Quaestiones Mathematicae 2003,26(3):247-265. 10.2989/16073600309486057
-semigroups and applications. Quaestiones Mathematicae 2003,26(3):247-265. 10.2989/16073600309486057Axler S, Bourdon P, Ramey W: Harmonic Function Theory, Graduate Texts in Mathematics. Volume 137. Springer, New York, NY, USA; 1992:xii+231.
Curtain RF, Zwart H: An Introduction to Infinite-Dimensional Linear Systems Theory, Texts in Applied Mathematics. Volume 21. Springer, New York, NY, USA; 1995:xviii+698.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Badraoui, S. Approximate Controllability of a Reaction-Diffusion System with a Cross-Diffusion Matrix and Fractional Derivatives on Bounded Domains. Bound Value Probl 2010, 281238 (2010). https://doi.org/10.1155/2010/281238
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/281238
 is a Hilbert space with the inner product
is a Hilbert space with the inner product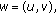 then we can define the linear operator
then we can define the linear operator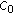 -Semigroup
-Semigroup As
As  , then there exist constants
, then there exist constants 
 reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006,2006(61):1-13.
reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006,2006(61):1-13. a reaction-diffusion system with cross diffusion matrix. to appear in Boundary Value Problems
a reaction-diffusion system with cross diffusion matrix. to appear in Boundary Value Problems -semigroups and applications. Quaestiones Mathematicae 2003,26(3):247-265. 10.2989/16073600309486057
-semigroups and applications. Quaestiones Mathematicae 2003,26(3):247-265. 10.2989/16073600309486057