- Research Article
- Open access
- Published:
Optimal Conditions for Maximum and Antimaximum Principles of the Periodic Solution Problem
Boundary Value Problems volume 2010, Article number: 410986 (2010)
Abstract
Given a periodic, integrable potential  , we will study conditions on
, we will study conditions on  so that the operator
so that the operator  admits the maximum principle or the antimaximum principle with respect to the periodic boundary condition. By exploiting Green functions, eigenvalues, rotation numbers, and their estimates, we will give several optimal conditions.
admits the maximum principle or the antimaximum principle with respect to the periodic boundary condition. By exploiting Green functions, eigenvalues, rotation numbers, and their estimates, we will give several optimal conditions.
1. Introduction and Main Results
Maximum Principle (MP) and AntiMaximum Principle (AMP) are fundamental tools in many problems. Generally speaking, criteria for MP and AMP are related to the location of relevant eigenvalues. See, for example, [1–5]. We also refer the reader to Campos et al. [6] for a recent abstract setting of MP and AMP.
In this paper we are studying criteria of MP and AMP for the periodic solution problem of ODEs. For such a problem, MP and AMP are not only related to periodic eigenvalues, but also to antiperiodic eigenvalues. Though there exist several sufficient conditions of MP and AMP for the periodic solution problem in literature like [7–9] (for a brief explanation to these conditions, see Section 4.3), an optimal characterization on MP and AMP is not available. The main aim of this paper is to give several optimal criteria of MP and AMP of the periodic solution problem of ODEs which are expressed using eigenvalues, Green functions, or rotation numbers.
Mathematically, let  be the circle of length
be the circle of length  . Given a
. Given a  -periodic potential
-periodic potential  , which defines a linear differential operator
, which defines a linear differential operator  by
by

we say that  admits the antimaximum principle if
admits the antimaximum principle if
(i) is invertible, and, moreover,
is invertible, and, moreover,
(ii)for any  with
with  , one has
, one has  . Here
. Here  means that
means that  a.e.
a.e.  and
and  on a subset of positive measure.
on a subset of positive measure.
In an abstract setting, these mean that  is a strictly positive operator with respect to the ordering
is a strictly positive operator with respect to the ordering  defined by
defined by  a.e.
a.e.  .
.
In terminology of differential equations,  admits AMP if and only if
admits AMP if and only if
(i)for any  , the following equation:
, the following equation:

has a unique  -periodic solution
-periodic solution  , and, moreover,
, and, moreover,
(ii)if  , one has
, one has  for all
for all  .
.
We say that  admits the maximum principle if
admits the maximum principle if  for all
for all  such that
such that  .
.
Using periodic and antiperiodic eigenvalues of Hill's equations [10, 11], we will obtain the following complete characterizations on MP and AMP.
Theorem 1.1.
Let  . Then
. Then  admits MP iff
admits MP iff  , and
, and  admits AMP iff
admits AMP iff  .
.
Here  and
and  are the smallest
are the smallest  -periodic and the smallest
-periodic and the smallest  -antiperiodic eigenvalues of
-antiperiodic eigenvalues of

respectively. For the precise meaning of these eigenvalues, see Section 2.2.
Given an arbitrary potential  , by introducing the parameterized potentials
, by introducing the parameterized potentials  ,
,  , Theorem 1.1 can be stated as follows.
, Theorem 1.1 can be stated as follows.
Theorem 1.2.
Let  . Then
. Then  admits MP iff
admits MP iff  , and
, and  admits AMP iff
admits AMP iff  .
.
We will also use Green functions to give complete characterizations on MP and AMP of  . See Theorem 4.1 and Corollary 4.4.
. See Theorem 4.1 and Corollary 4.4.
The paper is organized as follows. In Section 2, we will briefly introduce some concepts on Hill's equations [10, 12, 13], including the Poincaré matrixes  , eigenvalues
, eigenvalues  and rotation numbers
and rotation numbers  and oscillation of solutions. In Section 3, we will use the Poincaré matrixes and fundamental matrix solutions to give the formula of the Green functions
and oscillation of solutions. In Section 3, we will use the Poincaré matrixes and fundamental matrix solutions to give the formula of the Green functions  of the periodic solution problem (1.2). We will introduce for each potential
of the periodic solution problem (1.2). We will introduce for each potential  two matrixes,
two matrixes,  and
and  , and two functions,
, and two functions,  and
and  . They are related with the Poincaré matrix
. They are related with the Poincaré matrix  and the Green function
and the Green function  , respectively. Some remarkable properties on these new objects will be established.
, respectively. Some remarkable properties on these new objects will be established.
Section 4 is composed of three subsections. At first, in Section 4.1, we will use the sign of Green functions  to establish in Theorem 4.1 and Corollary 4.4 optimal conditions for MP and AMP. Then, in Section 4.2, we will use eigenvalues to give a complete description for the sign of Green functions. The proofs of Theorems 1.1 and 1.2 will be given. One may notice that in the deduction of the sign of Green functions, besides eigenvalues, rotation numbers, and oscillation of solutions, some important estimates on Poincaré matrixes in [10, 12] will be used. Moreover, in the deduction of AMP, a very remarkable reduction for elliptic Hill's equations by Ortega [14, 15] is effectively used to simplify the argument. Note that such a reduction is originally used to deduce the formula for the first Birkhoff twist coefficient of periodic solutions of nonlinear, scalar Newtonian equations. Finally, in Section 4.3, we will outline how the known sufficient conditions on AMP can be easily deduced from Theorem 1.1.
to establish in Theorem 4.1 and Corollary 4.4 optimal conditions for MP and AMP. Then, in Section 4.2, we will use eigenvalues to give a complete description for the sign of Green functions. The proofs of Theorems 1.1 and 1.2 will be given. One may notice that in the deduction of the sign of Green functions, besides eigenvalues, rotation numbers, and oscillation of solutions, some important estimates on Poincaré matrixes in [10, 12] will be used. Moreover, in the deduction of AMP, a very remarkable reduction for elliptic Hill's equations by Ortega [14, 15] is effectively used to simplify the argument. Note that such a reduction is originally used to deduce the formula for the first Birkhoff twist coefficient of periodic solutions of nonlinear, scalar Newtonian equations. Finally, in Section 4.3, we will outline how the known sufficient conditions on AMP can be easily deduced from Theorem 1.1.
2. Basic Facts on Hill's Equations
2.1. Fundamental Solutions and Poincaré Matrixes
Given  , let us introduce some basic concepts on the Hill's equation
, let us introduce some basic concepts on the Hill's equation

Let  ,
,  , be the fundamental solutions of (2.1), that is,
, be the fundamental solutions of (2.1), that is,  are solutions satisfying the initial values
are solutions satisfying the initial values

The fundamental matrix solution of (2.1) is

The Liouville theorem asserts that  . That is,
. That is,

the symplectic group of  .
.
The Poincaré matrix of (2.1) is

In particular,

The Floquet multipliers of (2.1) are eigenvalues  of
of  . Then
. Then  , following from (2.6).
, following from (2.6).
We say that (2.1) is elliptic, hyperbolic or parabolic, respectively, if  and
and  ,
,  , or
, or  , respectively. We write the sets of those potentials as
, respectively. We write the sets of those potentials as  ,
,  and
and  , respectively.
, respectively.
By introducing the trace

we have the following classification.
Lemma 2.1 (see [10]).
Equaqtion (2.1) is elliptic, hyperbolic, or parabolic, iff  ,
,  , or
, or  , respectively. In particular,
, respectively. In particular,  implies that
implies that  .
.
Proof.
We need to prove the last conclusion. Suppose that  . If
. If  , we have
, we have  and
and  . These are impossible.
. These are impossible.
2.2. Eigenvalues, Rotation Numbers, and Oscillation of Solutions
Given  , consider eigenvalue problems of (1.3) with respect to the
, consider eigenvalue problems of (1.3) with respect to the  -periodic boundary condition
-periodic boundary condition

or with respect to the  -antiperiodic boundary condition
-antiperiodic boundary condition

It is well known that one has (real) sequences

such that
(i) and
and  as
as  ;
;
(ii) is an eigenvalue of problem (1.3)–(2.8) (of problem (1.3)–(2.9), resp.) iff
is an eigenvalue of problem (1.3)–(2.8) (of problem (1.3)–(2.9), resp.) iff  or
or  where
where  is even (
is even ( is odd, resp.). Here
is odd, resp.). Here  is void;
is void;
(iii) is a periodic (an antiperiodic, resp.) eigenvalue of (1.3) iff
is a periodic (an antiperiodic, resp.) eigenvalue of (1.3) iff

For these general results, one can refer to [10, 11]. Note that in [10] only piecewise continuous potentials are considered. However, these are also true for  potentials. See [12, 16].
potentials. See [12, 16].
Denote

Using periodic eigenvalues or traces of Poincaré matrixes, the set  can be characterized as
can be characterized as

Here the equivalence of (2.13) follows from (2.11).
Let us introduce the rotation number for (2.1). Under the transformation  , we know from (2.1) that the argument
, we know from (2.1) that the argument  satisfies
satisfies

Given  . Define
. Define

where  is any solution of (2.14). The limit (2.15) does exist and is independent of the choice of
is any solution of (2.14). The limit (2.15) does exist and is independent of the choice of  . Such a number
. Such a number  is called the rotation number of (2.1). An alternative definition for (2.15) is
is called the rotation number of (2.1). An alternative definition for (2.15) is

where  is any nonzero solution of (2.1).
is any nonzero solution of (2.1).
The connection between eigenvalues and oscillation of solutions is as follows.
Lemma 2.3.
Given  , consider the parameterized Hill's equations (1.3) where
, consider the parameterized Hill's equations (1.3) where  . Then
. Then
(i)in case  , any nonzero solution
, any nonzero solution  of (1.3) is nonoscillatory. More precisely,
of (1.3) is nonoscillatory. More precisely,  has at most one zero in the whole line
has at most one zero in the whole line 
(ii)in case  , any nonzero solution
, any nonzero solution  of (1.3) is oscillatory. More precisely,
of (1.3) is oscillatory. More precisely,  has infinitely many zeros.
has infinitely many zeros.
2.3. Continuous Dependence on Potentials
Associated with the Hill's equation (2.1), we have the objects  ,
,  ,
,  , and
, and  . All are determined by the potential
. All are determined by the potential  . It is a classical result that all of these objects are continuously dependent on
. It is a classical result that all of these objects are continuously dependent on  when the
when the  topology
topology  is considered. For the fundamental matrix solutions, this can be stated as follows.
is considered. For the fundamental matrix solutions, this can be stated as follows.
Given  , the following mapping:
, the following mapping:

is continuously Frechét differentiable. Moreover, the Frechét derivatives can be expressed using  .
.
In the space  , one has also the weak topology
, one has also the weak topology  which is defined by
which is defined by

In a recent paper [20], Zhang has proved that these objects have stronger dependence on potentials  . Some statements of these facts are as follows.
. Some statements of these facts are as follows.
Lemma 2.5 (Zhang [20]).
The following mapping is continuous:

Moreover, the following (nonlinear) functionals:

are also continuous in  .
.
From this lemma, the set  is open in
is open in  and in
and in  .
.
3. Green Functions and Their Variants
3.1. Green Functions
Let  . Then, for each
. Then, for each  , (1.2) has a unique solution
, (1.2) has a unique solution  satisfying the
satisfying the  -periodic boundary condition (2.8). From the Fredholm principle,
-periodic boundary condition (2.8). From the Fredholm principle,  can be represented as
can be represented as

where

is the so-called Green function of the periodic solution problem (1.2)–(2.8). Another definition of the Green function is

Here  is the
is the  -periodic unit Dirac measure located at
-periodic unit Dirac measure located at  . The Green function
. The Green function  can be expressed using
can be expressed using  and
and  as follows.
as follows.
Lemma 3.1.
Given  , we have the following results.
, we have the following results.
(i) is given by
is given by

(ii) is continuous in
is continuous in  and is symmetric
and is symmetric

Moreover,  can be extended to a continuous
can be extended to a continuous  -periodic function in both arguments, that is,
-periodic function in both arguments, that is,  ,
,  .
.
Proof.
-
(i)
Formula (3.4) can be found from related references. For completeness, let us give the proof.
Given  . By the constant-of-variant formula, solutions of (1.2) are given by
. By the constant-of-variant formula, solutions of (1.2) are given by

where  are constants. In order that
are constants. In order that  is
is  -periodic, it is necessary and sufficient that
-periodic, it is necessary and sufficient that  satisfies (2.8), that is,
satisfies (2.8), that is,  satisfy
satisfy

Since  , we know that
, we know that

Hence

where  has the form of (3.4).
has the form of (3.4).
-
(ii)
From formula (3.4), the symmetry (3.5) is obvious. Moreover,
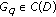 . Finally, let us show that
. Finally, let us show that 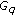 can be extended to a continuous function on the torus
can be extended to a continuous function on the torus 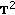 . By using (2.2), (2.5), and (2.6), one has from (3.4)
. By using (2.2), (2.5), and (2.6), one has from (3.4)  (3.10)
(3.10)
By the symmetry (3.5), one has

Thus  can be understood as a function on
can be understood as a function on  .
.
In general,  is not differentiable at the diagonal
is not differentiable at the diagonal  .
.
3.2. Two Matrixes and Two Functions
Let us introduce, for any  , the following two matrixes:
, the following two matrixes:


Note that  is a symmetric matrix. Using the Poincaré matrix
is a symmetric matrix. Using the Poincaré matrix  ,
,  and
and  can be rewritten as
can be rewritten as

Here denotes the transpose of matrixes,
denotes the transpose of matrixes,  is the identity matrix, and
is the identity matrix, and

Some results on  and
and  and their connections with the Poincaré matrix
and their connections with the Poincaré matrix  are as follows. All of them can be verified directly.
are as follows. All of them can be verified directly.
Lemma 3.2.
Given  , let
, let  ,
,  , and
, and  . Then
. Then




From equalities in Lemma 3.2, we have the following statements.
Lemma 3.3.
Given  , then
, then
(i) is nonsingular iff
is nonsingular iff  , and
, and  is nonsingular iff
is nonsingular iff  ;
;
(ii)Equation (2.1) is elliptic, hyperbolic, or parabolic, iff  ,
,  , or
, or  , respectively.
, respectively.
Since  is
is  -periodic, one has the following equality for the fundamental matrix solution
-periodic, one has the following equality for the fundamental matrix solution

Let us introduce the vector-valued function

which is composed by the fundamental solutions  of (2.1). Then
of (2.1). Then

Hence

In the following, we use  to denote the Euclidean inner product on
to denote the Euclidean inner product on  . In case
. In case  , the Green function
, the Green function  in (3.4) can be rewritten as
in (3.4) can be rewritten as

Here  is as in (3.12). Note that
is as in (3.12). Note that  .
.
Suggested by (3.24), let us introduce for any  two functions
two functions


where  and
and  are as in (3.12) and (3.13). Note that these functions are well defined on the whole plane and the whole line, respectively. Some properties are as follows.
are as in (3.12) and (3.13). Note that these functions are well defined on the whole plane and the whole line, respectively. Some properties are as follows.
Lemma 3.4.
For any  , one has
, one has



Proof.
We need only to verify (3.27) for the case  . To this end, one has
. To this end, one has

For (3.28), we have

Finally, equality (3.29) follows simply from (3.26) and (3.27).
We remark that, in general,  is not true for
is not true for  . Note that (3.29) asserts that
. Note that (3.29) asserts that  is
is  -periodic. Some further properties on
-periodic. Some further properties on  are as follows.
are as follows.
Lemma 3.5.
-
(i)
Let
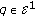 . Then
. Then 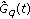 does not have any zero and therefore does not change sign.
does not have any zero and therefore does not change sign. -
(ii)
Let
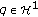 . Then
. Then 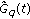 has only nondegenerate zeros, if they exist.
has only nondegenerate zeros, if they exist. -
(iii)
Let
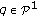 . Then
. Then 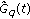 has a constant sign. Moreover,
has a constant sign. Moreover, 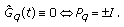 (3.32)
(3.32)
Proof.
-
(i)
Suppose that
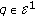 is elliptic. We have
is elliptic. We have 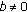 from Lemma 2.1. By (3.17),
from Lemma 2.1. By (3.17), 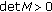 . Hence the symmetric matrix
. Hence the symmetric matrix  is either positive definite or negative definite, according to
is either positive definite or negative definite, according to  or
or  . Since
. Since  for all
for all 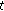 , we know that
, we know that  on
on 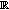 .
. -
(ii)
Suppose that
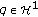 . We have
. We have  . Thus there exists an orthogonal transformation
. Thus there exists an orthogonal transformation 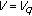 such that
such that 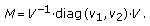 (3.33)
(3.33)
Here  are eigenvalues of
are eigenvalues of  and satisfy
and satisfy  . Then
. Then

Note that  is also a system of fundamental solutions of (2.1). As
is also a system of fundamental solutions of (2.1). As  , we have
, we have

where

Note that  is a linearly independent system of solutions of (2.1). From (3.35),
is a linearly independent system of solutions of (2.1). From (3.35),  has only nondegenerate zeros, if they exist. In fact, suppose that
has only nondegenerate zeros, if they exist. In fact, suppose that  , say
, say  . We have
. We have  and
and  . Thus
. Thus

-
(iii)
Suppose that
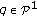 . We have
. We have 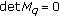 . Then one eigenvalue of
. Then one eigenvalue of 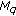 is
is  and another is
and another is 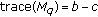 . In this case,
. In this case, 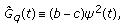 (3.38)
(3.38)
where  is a nonzero solution of (2.1). This shows that
is a nonzero solution of (2.1). This shows that  does not change sign.
does not change sign.
We distinguish two cases.
(i) is stable-parabolic, that is,
is stable-parabolic, that is,  . In this case, one has
. In this case, one has  and
and  .
.
(ii) is unstable-parabolic, that is,
is unstable-parabolic, that is,  . In this case, we assert that
. In this case, we assert that  .
.
Otherwise, assume  . Then
. Then

Since  and
and  , we obtain
, we obtain  . Hence
. Hence  and
and  . Moreover,
. Moreover,  . Thus
. Thus  and
and  is stable-parabolic. In conclusion, for unstable-parabolic case, we have
is stable-parabolic. In conclusion, for unstable-parabolic case, we have  . Now it follows from (3.38) that
. Now it follows from (3.38) that  . As proved before,
. As proved before,  does not change sign. Moreover, it is easy to see from (3.38) that all zeros of
does not change sign. Moreover, it is easy to see from (3.38) that all zeros of  must be degenerate, if they exist.
must be degenerate, if they exist.
From these, (3.32) is clear.
4. Optimal Conditions for MP and AMP
4.1. Complete Characterizations of MP and AMP Using Green Functions
Using Green functions  , we have the following characterizations on MP and AMP.
, we have the following characterizations on MP and AMP.
Theorem 4.1.
Let  with the Green function
with the Green function  . Then
. Then  admits MP iff
admits MP iff  and
and 
Proof.
We give only the proof for AMP.
The sufficiency is as follows. Suppose that  satisfies
satisfies  . Then, for any
. Then, for any  , it is easy to see from (3.1) that
, it is easy to see from (3.1) that  for all
for all  . We will show that
. We will show that  for all
for all  and consequently (1.2) admits AMP.
and consequently (1.2) admits AMP.
Otherwise, suppose that  for some
for some  , that is,
, that is,

Since  , we have necessarily
, we have necessarily

From (3.24), we know that
(i)on the interval  ,
,

is a solution of (2.1);
(ii)on the interval  ,
,

is also a solution of (2.1).
We assert that these solutions are nonzero when the corresponding intervals are nontrivial. As  is composed of two linearly independent solutions
is composed of two linearly independent solutions  , the nontriviality of these solutions is the same as
, the nontriviality of these solutions is the same as

which are evident because  and (3.16) shows that
and (3.16) shows that  .
.
From the above assertion, we know that  (=
(= has only isolated zeros for
has only isolated zeros for  . As
. As  , we have
, we have  , a contradiction with (4.2).
, a contradiction with (4.2).
For the necessity, let us assume that  . Then one has some
. Then one has some  so that
so that  . Hence one has some
. Hence one has some  such that
such that

Let us choose  such that
such that

Then  . However, the corresponding periodic solution
. However, the corresponding periodic solution  of (1.2) satisfies
of (1.2) satisfies

Hence  does not admit AMP.
does not admit AMP.
In order to apply Theorem 4.1, it is important to compute the signs of the following nonlinear functionals of potentials:

To this end, let us establish some relation between  and
and  .
.
For general  , denote
, denote

Suppose that  so that
so that  is meaningful. We assert that
is meaningful. We assert that

In fact, for  , the first case of (4.11) follows immediately from the defining equalities (3.24), (3.25), and (4.10). On the other hand, for
, the first case of (4.11) follows immediately from the defining equalities (3.24), (3.25), and (4.10). On the other hand, for  , from the second case of (3.24), one has
, from the second case of (3.24), one has

Hence (4.11) is also true for this case.
By introducing the domain

and the following nonlinear functionals 

we have the following statements.
Lemma 4.2.
There hold, for all  ,
,

Proof.
We only prove the first equality of (4.15) because the second one is similar. By (4.11), for any  , we have
, we have

Hence

Consequently,

This is just (4.15) because  .
.
Remark 4.3.
-
(i)
The functionals
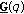 and
and  are well defined for all potentials
are well defined for all potentials  . Moreover, by (4.15),
. Moreover, by (4.15), 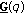 and
and 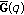 have the same signs with the functionals in (4.9).
have the same signs with the functionals in (4.9). -
(ii)
Compared with the defining formulas in (4.9), the novelty of formulas in (4.14) is that when
 is fixed,
is fixed, 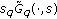 is a solution of (2.1), while when
is a solution of (2.1), while when 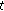 is fixed,
is fixed, 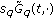 is also a solution of (2.1). A similar observation is used in [8] as well.
is also a solution of (2.1). A similar observation is used in [8] as well. -
(iii)
Due to the factor
 which is zero at those
which is zero at those 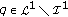 ,
, 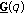 and
and 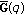 are in general discontinuous at
are in general discontinuous at  . However,
. However, 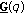 and
and 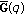 are continuous at
are continuous at 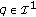 in the
in the 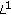 topology
topology  or even in the weak topology
or even in the weak topology  . See Lemmas 2.4 and 2.5.
. See Lemmas 2.4 and 2.5.
By Lemma 4.2, Theorem 4.1 can be restated as follows.
Corollary 4.4.
Let  . Then
. Then  admits MP iff
admits MP iff  , and
, and  admits AMP iff
admits AMP iff  .
.
4.2. Complete Characterizations of MP and AMP Using Eigenvalues
Lemma 4.5.
Let  be such that
be such that  . Then
. Then  and
and  admits MP.
admits MP.
Proof.
For simplicity, denote

For any  , one has
, one has  and
and  . See [10]. Thus
. See [10]. Thus  . In the following let us fix any
. In the following let us fix any  .
.
Step 1.
We assert that

Since  , we can use the representation (3.35) for
, we can use the representation (3.35) for  where
where  and
and  are nonzero solutions of (2.1). Since
are nonzero solutions of (2.1). Since  , both
, both  have at most one zero. See Lemma 2.3. Hence
have at most one zero. See Lemma 2.3. Hence  has at most two zeros. However, as
has at most two zeros. However, as  is
is  -periodic,
-periodic,  does not have any zero. This proves (4.20).
does not have any zero. This proves (4.20).
Step 2.
We assert that

If (4.21) is false, there exists  such that
such that  . By introducing
. By introducing

one has

We know from (3.28) and (4.20) that  satisfies
satisfies

This shows that  . Since
. Since  is a nonzero solution of (2.1), (4.23) implies
is a nonzero solution of (2.1), (4.23) implies

Since  has the same nonzero value at the end-points of the interval
has the same nonzero value at the end-points of the interval  , it is easy to see from (4.24) and (4.25) that
, it is easy to see from (4.24) and (4.25) that  must have another zero
must have another zero  which is different from
which is different from  . Consequently, the solution
. Consequently, the solution  of (2.1) has at least zeros
of (2.1) has at least zeros  and
and  . This is impossible because
. This is impossible because  . See Lemma 2.3.
. See Lemma 2.3.
Step 3.
Let us notice that

We assert that

To prove (4.27), let us fix  and consider
and consider  , where
, where  . Then
. Then  . Since
. Since  ,
,  for all
for all  . When
. When  ,
,  can be estimated. The basic idea is to consider (1.3) as a perturbation of the equation
can be estimated. The basic idea is to consider (1.3) as a perturbation of the equation

for which

It is well known that the difference  can be controlled by the norm of the potential
can be controlled by the norm of the potential  when
when  . For piecewise continuous and
. For piecewise continuous and  potentials, see [10] and [12], respectively. Similar estimates are also true for
potentials, see [10] and [12], respectively. Similar estimates are also true for  potentials. In fact, these can be generalized to Hill's equations with coefficients being measures [16]. We quote from [12, Theorem
potentials. In fact, these can be generalized to Hill's equations with coefficients being measures [16]. We quote from [12, Theorem  ] the following result:
] the following result:

Hence

as  . We conclude
. We conclude

On the other hand, by (4.21) and (4.26),

Moreover, it follows from Lemma 2.4 that  is continuous in
is continuous in  . Thus (4.27) follows simply from (4.32) and (4.33).
. Thus (4.27) follows simply from (4.32) and (4.33).
Step 4.
Since  ,
,  . It follows from (4.21), (4.26), and (4.27) that, for all
. It follows from (4.21), (4.26), and (4.27) that, for all  ,
,  has the same sign with
has the same sign with  . Thus
. Thus  . By Corollary 4.4,
. By Corollary 4.4,  admits MP.
admits MP.
Lemma 4.6.
Suppose that  satisfies
satisfies  and
and  . Then
. Then  and
and  admits AMP.
admits AMP.
Proof.
For simplicity, denote

Recall from [11] that eigenvalues  and
and  can be characterized using rotation numbers by
can be characterized using rotation numbers by

Here  is arbitrary. Hence
is arbitrary. Hence

In the following, let  . We have
. We have  ,
,  and
and  . Now we argue as in the proof of Lemma 4.5. In this case, result (4.20) can be obtained from Lemma 3.5(i) because
. Now we argue as in the proof of Lemma 4.5. In this case, result (4.20) can be obtained from Lemma 3.5(i) because  . If (4.21) is false at some
. If (4.21) is false at some  , we have also
, we have also  . By letting
. By letting  be as in (4.22), one has also some
be as in (4.22), one has also some  such that
such that  and
and  . With loss of generality, let us assume that
. With loss of generality, let us assume that  . Notice that the solution
. Notice that the solution  of (2.1) has zeros
of (2.1) has zeros  and
and  . By the Sturm comparison theorem, any nonzero solution
. By the Sturm comparison theorem, any nonzero solution  of (2.1) has at least one zero in
of (2.1) has at least one zero in  . In particular, for any
. In particular, for any  ,
,  is a solution of (2.1). Hence there exists some
is a solution of (2.1). Hence there exists some  such that
such that

By equality (3.27),

Thus

From these, the distribution of zeros of the specific solution  satisfies
satisfies

By definition (2.16) for the rotation number, we obtain

a contradiction with the characterization of  . Thus (4.21) is also true for
. Thus (4.21) is also true for  .
.
Since  , we have from (4.21) and (4.26) that
, we have from (4.21) and (4.26) that  , because we will prove in Lemma 4.7 that
, because we will prove in Lemma 4.7 that  for all
for all  .
.
Note that  is the set of potentials which are in the first ellipticity zone. By Lemmas 2.1 or 3.5,
is the set of potentials which are in the first ellipticity zone. By Lemmas 2.1 or 3.5,  for all
for all  . It seems that there are several ways to deduce that
. It seems that there are several ways to deduce that  for all
for all  . However, some remarkable result on elliptic Hill's equations by Ortega [14, 15] can simplify the argument. Let us describe the result. Suppose that
. However, some remarkable result on elliptic Hill's equations by Ortega [14, 15] can simplify the argument. Let us describe the result. Suppose that  . Consider the temporal-spatial transformation
. Consider the temporal-spatial transformation

where  and
and  . Then (2.1) is transformed into a new Hill's equation
. Then (2.1) is transformed into a new Hill's equation

where  is now
is now  periodic. The result of Ortega shows that it is always possible to choose some
periodic. The result of Ortega shows that it is always possible to choose some  such that the Poincaré matrix
such that the Poincaré matrix  (of the period
(of the period  ) of (4.43) is a rigid rotation
) of (4.43) is a rigid rotation

See [15, Lemma  ] and [21]. We remark that such a result is very important to study the twist character and Lyapunov stability of periodic solutions of nonlinear Newtonian equations and planar Hamiltonian systems. See, for example, [14, 15, 21].
] and [21]. We remark that such a result is very important to study the twist character and Lyapunov stability of periodic solutions of nonlinear Newtonian equations and planar Hamiltonian systems. See, for example, [14, 15, 21].
Note that the transformation (4.42) does not change rotation numbers. Recall that the polar coordinates to define rotation numbers are

We see from (4.44) that  is related with
is related with  via
via

Hence

Lemma 4.7.
We assert that

Proof.
We first prove that  ,
,  , is invariant under transformations (4.42). In fact, it is well known that
, is invariant under transformations (4.42). In fact, it is well known that  and
and  are conjugate
are conjugate

for some  . Denote
. Denote

From (4.49), one has the explicit relation

Note that the quadratic form  is definite. See the proof of Lemma 3.5(i). Since
is definite. See the proof of Lemma 3.5(i). Since  , we have
, we have

Hence  is invariant under transformations (4.42).
is invariant under transformations (4.42).
Now (4.48) can be obtained as follows. Let  . Then
. Then  . By (4.47), the transformed potential
. By (4.47), the transformed potential  satisfies
satisfies  . By the invariance, we have the desired result (4.48).
. By the invariance, we have the desired result (4.48).
Lemma 4.8.
Suppose that  satisfies
satisfies  . Then
. Then  and
and  admits AMP.
admits AMP.
Proof.
Since  , we have
, we have  and
and  . See (2.11). Moreover, by (2.10), we have
. See (2.11). Moreover, by (2.10), we have  . Let
. Let  . Then
. Then  for all
for all  . We know from Lemma 4.6 that
. We know from Lemma 4.6 that  for
for  . Letting
. Letting  and noticing that
and noticing that  is continuous at
is continuous at  , we get
, we get

On the other hand, let us take an antiperiodic eigen function  of (2.1) associated with
of (2.1) associated with  . Denote by
. Denote by  the smallest nonnegative zero of
the smallest nonnegative zero of  . Then
. Then  . Moreover, both
. Moreover, both  and
and  are zeros of
are zeros of  because of the
because of the  -antiperiodicity of
-antiperiodicity of  . By the Sturm comparison theorem, the solution
. By the Sturm comparison theorem, the solution  of (2.1) must have some zero in
of (2.1) must have some zero in  . Hence
. Hence  . As
. As  , we obtain
, we obtain

In conclusion we have  .
.
Lemma 4.9.
Suppose that  satisfies
satisfies  . Then
. Then  does not admit neither MP nor AMP.
does not admit neither MP nor AMP.
Proof.
We need not to consider the case  because
because  is not invertible.
is not invertible.
In the following let us assume that  satisfies
satisfies  . Then
. Then  . The following is a modification of the last part of the proof of Lemma 4.8.
. The following is a modification of the last part of the proof of Lemma 4.8.
Let us take an antiperiodic eigenfunction  associated with
associated with  . Then the set of all zeros of
. Then the set of all zeros of  is
is  for some
for some  . Denote
. Denote

Then  is a nonzero solution of (2.1). Since
is a nonzero solution of (2.1). Since  , by applying the Sturm comparison theorem to
, by applying the Sturm comparison theorem to  and
and  , we know that
, we know that  must have some zero
must have some zero  in
in  , the interior of the interval
, the interior of the interval  because
because  and
and  are consecutive zeros of
are consecutive zeros of  . As
. As  , one must have
, one must have

Thus  changes sign near
changes sign near  . Consequently,
. Consequently,

Now Corollary 4.4 shows that  does not admit AMP. We have also
does not admit AMP. We have also

Hence  does not admit MP.
does not admit MP.
Due to the ordering (2.10) of eigenvalues, the statements in Theorems 1.1 and 1.2 are equivalent. Now let us give the proof of Theorem 1.2. Recall that  and
and  for all
for all  . By Lemma 4.5, if
. By Lemma 4.5, if  ,
,  admits MP. By Lemmas 4.6 and 4.8,
admits MP. By Lemmas 4.6 and 4.8,  admits AMP for
admits AMP for  . By Lemma 4.9,
. By Lemma 4.9,  does not admit MP nor AMP for
does not admit MP nor AMP for  . Using the ordering (2.10) for eigenvalues, we complete the proof of Theorem 1.2.
. Using the ordering (2.10) for eigenvalues, we complete the proof of Theorem 1.2.
From Lemmas 4.5, 4.6, 4.8, and 4.9, the sign of Green functions is clear in all cases.
Definition 4.10.
Given  , we say that
, we say that  admits strong antimaximum principle (SAMP) if
admits strong antimaximum principle (SAMP) if  admits AMP and, moreover, there exists
admits AMP and, moreover, there exists  such that
such that

Then we have the following complete characterizations for SAMP.
Theorem 4.11.
Let  . Then
. Then  admits SAMP iff
admits SAMP iff  iff
iff  .
.
4.3. Explicit Conditions for AMP
Let us recall some known sufficient conditions for AMP.
Lemma 4.12 (Torres and Zhang [9]).
Suppose that  satisfies the following two conditions:
satisfies the following two conditions:


Then  admits AMP.
admits AMP.
In the proof there, the positiveness condition (4.60) is technically used extensively. Some optimal estimates on condition (4.61) can be found in Zhang and Li [22]. For an exponent  , let us introduce the following Sobolev constant:
, let us introduce the following Sobolev constant:

Here  . These constants
. These constants  can be explicitly expressed using the Gamma function of Euler. The following lower bound for
can be explicitly expressed using the Gamma function of Euler. The following lower bound for  is established in [22]:
is established in [22]:

where  . Hence one sufficient condition for (4.61) is
. Hence one sufficient condition for (4.61) is

Now such an  condition (4.64) is quite standard in literature like [8, 23], because in case
condition (4.64) is quite standard in literature like [8, 23], because in case  , (4.64) reads as the classical condition
, (4.64) reads as the classical condition

In order to overcome the technical assumption (4.60) on positiveness of  , one observation is as follows.
, one observation is as follows.
Lemma 4.13 (Torres [8, Theorem  ]).
]).
Let  . Suppose that all gaps of consecutive zeros of all nonzero solutions
. Suppose that all gaps of consecutive zeros of all nonzero solutions  of (2.1) are strictly greater than the period 1. Then the Green function
of (2.1) are strictly greater than the period 1. Then the Green function  has a constant sign.
has a constant sign.
By Theorem 4.1 of this paper, one sees that the hypothesis in Lemma 4.13 on solutions of (2.1) can yield MP or AMP. Combining ideas from [8, 9, 22], Cabada and Cid have overcome the positiveness condition (4.60) to obtain the following criteria.
Lemma 4.14 (Cabada and Cid [7, Theorem  ]).
]).
Suppose that  satisfies the following two conditions:
satisfies the following two conditions:


Then  admits AMP.
admits AMP.
Very recently, Cabada et al. [24, 25] have generalized criteria (4.66)-(4.67) for  to AMP of the periodic solutions of the so-called
to AMP of the periodic solutions of the so-called  -Laplacian problem
-Laplacian problem

with the constants  being replaced by more general Sobolev constants [26].
being replaced by more general Sobolev constants [26].
We end the paper with some remarks.
-
(i)
Recall the following trivial upper bound:
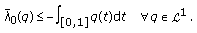 (4.69)
(4.69)
See, for example, [26]. Criteria (4.66)-(4.67) can be deduced from Theorem 1.1 with the help of estimates (4.63) and (4.69). In fact, by Theorem 4.11, conditions (4.66) and (4.67) guarantee that  admits SAMP. For AMP of
admits SAMP. For AMP of  , condition (4.67) can be improved as
, condition (4.67) can be improved as

Theorem 1.1 shows that condition (4.61) is optimal, while the complete generalization of condition (4.60) is  .
.
-
(ii)
It is also possible to construct many potentials
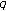 for which
for which 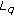 admits AMP, while (4.70) is violated. For example, let
admits AMP, while (4.70) is violated. For example, let 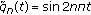 and
and 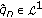 be defined by
be defined by  (4.71)
(4.71)
Then  and the Riemann-Lebesgue lemma shows that
and the Riemann-Lebesgue lemma shows that  in
in  , where
, where  is arbitrarily fixed. In particular, it follows from Lemma 2.5 that
is arbitrarily fixed. In particular, it follows from Lemma 2.5 that

Since

we conclude that for  with
with  ,
,  admits AMP. However, when
admits AMP. However, when  is large and
is large and  ,
,

is also large. Hence  does not satisfy (4.70).
does not satisfy (4.70).
-
(iii)
Notice that the lower bound (4.63) has actually shown that, under (4.67) ((4.70), resp.), the gaps of consecutive zeros of all nonzero solutions
 of (2.1) are
of (2.1) are 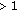 (
(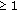 , resp.). However, for those potentials as in Theorem 1.1, zeros of solutions of (2.1) may not be so evenly distributed. This is the difference between the sufficient conditions in this subsection and our optimal conditions given in Theorem 1.1.
, resp.). However, for those potentials as in Theorem 1.1, zeros of solutions of (2.1) may not be so evenly distributed. This is the difference between the sufficient conditions in this subsection and our optimal conditions given in Theorem 1.1.
References
Barteneva IV, Cabada A, Ignatyev AO: Maximum and anti-maximum principles for the general operator of second order with variable coefficients. Applied Mathematics and Computation 2003,134(1):173-184. 10.1016/S0096-3003(01)00280-6
Grunau H-C, Sweers G: Optimal conditions for anti-maximum principles. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 2001,30(3-4):499-513.
Mawhin J, Ortega R, Robles-Pérez AM: Maximum principles for bounded solutions of the telegraph equation in space dimensions two and three and applications. Journal of Differential Equations 2005,208(1):42-63. 10.1016/j.jde.2003.11.003
Pinchover Y: Maximum and anti-maximum principles and eigenfunctions estimates via perturbation theory of positive solutions of elliptic equations. Mathematische Annalen 1999,314(3):555-590. 10.1007/s002080050307
Takác P: An abstract form of maximum and anti-maximum principles of Hopf's type. Journal of Mathematical Analysis and Applications 1996,201(2):339-364. 10.1006/jmaa.1996.0259
Campos J, Mawhin J, Ortega R: Maximum principles around an eigenvalue with constant eigenfunctions. Communications in Contemporary Mathematics 2008,10(6):1243-1259. 10.1142/S021919970800323X
Cabada A, Cid JÁ: On the sign of the Green's function associated to Hill's equation with an indefinite potential. Applied Mathematics and Computation 2008,205(1):303-308. 10.1016/j.amc.2008.08.008
Torres PJ: Existence of one-signed periodic solutions of some second-order differential equations via a Krasnoselskii fixed point theorem. Journal of Differential Equations 2003,190(2):643-662. 10.1016/S0022-0396(02)00152-3
Torres PJ, Zhang M: A monotone iterative scheme for a nonlinear second order equation based on a generalized anti-maximum principle. Mathematische Nachrichten 2003, 251: 101-107. 10.1002/mana.200310033
Magnus W, Winkler S: Hill's Equation. Dover, New York, NY, USA; 1979:viii+129.
Zhang M:The rotation number approach to eigenvalues of the one-dimensional
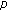 -Laplacian with periodic potentials. Journal of the London Mathematical Society. Second Series 2001,64(1):125-143. 10.1017/S0024610701002277
-Laplacian with periodic potentials. Journal of the London Mathematical Society. Second Series 2001,64(1):125-143. 10.1017/S0024610701002277Pöschel J, Trubowitz E: The Inverse Spectrum Theory. Academic Press, New York, NY, USA; 1987.
Zettl A: Sturm-Liouville Theory, Mathematical Surveys and Monographs. Volume 121. American Mathematical Society, Providence, RI, USA; 2005:xii+328.
Ortega R: The twist coefficient of periodic solutions of a time-dependent Newton's equation. Journal of Dynamics and Differential Equations 1992,4(4):651-665. 10.1007/BF01048263
Ortega R: Periodic solutions of a Newtonian equation: stability by the third approximation. Journal of Differential Equations 1996,128(2):491-518. 10.1006/jdeq.1996.0103
Meng G, Zhang M:Measure differential equations, II, Continuity of eigenvalues in measures with
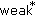 topology. preprint
topology. preprintFeng H, Zhang M: Optimal estimates on rotation number of almost periodic systems. Zeitschrift für Angewandte Mathematik und Physik 2006,57(2):183-204. 10.1007/s00033-005-0020-y
Johnson R, Moser J: The rotation number for almost periodic potentials. Communications in Mathematical Physics 1982,84(3):403-438. 10.1007/BF01208484
Johnson R, Moser J: Erratum: "The rotation number for almost periodic potentials" [Comm. Math. Phys. vol. 84 (1982), no. 3, 403–438]. Communications in Mathematical Physics 1983,90(2):317-318. 10.1007/BF01205510
Zhang M: Continuity in weak topology: higher order linear systems of ODE. Science in China. Series A 2008,51(6):1036-1058. 10.1007/s11425-008-0011-5
Chu J, Lei J, Zhang M: The stability of the equilibrium of a nonlinear planar system and application to the relativistic oscillator. Journal of Differential Equations 2009,247(2):530-542. 10.1016/j.jde.2008.11.013
Zhang M, Li W:A Lyapunov-type stability criterion using
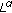 norms. Proceedings of the American Mathematical Society 2002,130(11):3325-3333. 10.1090/S0002-9939-02-06462-6
norms. Proceedings of the American Mathematical Society 2002,130(11):3325-3333. 10.1090/S0002-9939-02-06462-6Chu J, Nieto JJ: Recent existence results for second-order singular periodic differential equations. Boundary Value Problems 2009, 2009:-20.
Cabada A, Cid JÁ, Tvrdý M:A generalized anti-maximum principle for the periodic one-dimensional
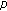 -Laplacian with sign-changing potential. Nonlinear Analysis: Theory, Methods & Applications 2010,72(7-8):3436-3446. 10.1016/j.na.2009.12.028
-Laplacian with sign-changing potential. Nonlinear Analysis: Theory, Methods & Applications 2010,72(7-8):3436-3446. 10.1016/j.na.2009.12.028Cabada A, Lomtatidze A, Tvrdý M: Periodic problem involving quasilinear differential operator and weak singularity. Advanced Nonlinear Studies 2007,7(4):629-649.
Zhang M:Certain classes of potentials for
 -Laplacian to be non-degenerate. Mathematische Nachrichten 2005,278(15):1823-1836. 10.1002/mana.200410342
-Laplacian to be non-degenerate. Mathematische Nachrichten 2005,278(15):1823-1836. 10.1002/mana.200410342
Acknowledgments
The author is supported by the Major State Basic Research Development Program (973 Program) of China (no. 2006CB805903), the Doctoral Fund of Ministry of Education of China (no. 20090002110079), the Program of Introducing Talents of Discipline to Universities (111 Program) of Ministry of Education and State Administration of Foreign Experts Affairs of China (2007), and the National Natural Science Foundation of China (no. 10531010).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, M. Optimal Conditions for Maximum and Antimaximum Principles of the Periodic Solution Problem. Bound Value Probl 2010, 410986 (2010). https://doi.org/10.1155/2010/410986
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/410986
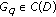 . Finally, let us show that
. Finally, let us show that 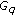 can be extended to a continuous function on the torus
can be extended to a continuous function on the torus 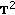 . By using (2.2), (2.5), and (2.6), one has from (3.4)
. By using (2.2), (2.5), and (2.6), one has from (3.4) 
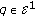 . Then
. Then 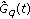 does not have any zero and therefore does not change sign.
does not have any zero and therefore does not change sign.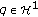 . Then
. Then 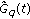 has only nondegenerate zeros, if they exist.
has only nondegenerate zeros, if they exist.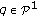 . Then
. Then 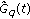 has a constant sign. Moreover,
has a constant sign. Moreover, 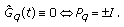
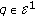 is elliptic. We have
is elliptic. We have 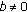 from Lemma 2.1. By (3.17),
from Lemma 2.1. By (3.17), 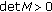 . Hence the symmetric matrix
. Hence the symmetric matrix  is either positive definite or negative definite, according to
is either positive definite or negative definite, according to  or
or  . Since
. Since  for all
for all 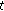 , we know that
, we know that  on
on 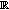 .
.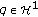 . We have
. We have  . Thus there exists an orthogonal transformation
. Thus there exists an orthogonal transformation 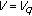 such that
such that 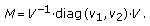
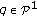 . We have
. We have 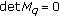 . Then one eigenvalue of
. Then one eigenvalue of 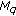 is
is  and another is
and another is 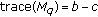 . In this case,
. In this case, 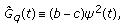
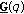 and
and  are well defined for all potentials
are well defined for all potentials  . Moreover, by (4.15),
. Moreover, by (4.15), 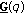 and
and 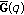 have the same signs with the functionals in (4.9).
have the same signs with the functionals in (4.9). is fixed,
is fixed, 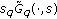 is a solution of (2.1), while when
is a solution of (2.1), while when 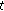 is fixed,
is fixed, 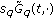 is also a solution of (2.1). A similar observation is used in [
is also a solution of (2.1). A similar observation is used in [ which is zero at those
which is zero at those 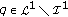 ,
, 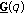 and
and 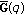 are in general discontinuous at
are in general discontinuous at  . However,
. However, 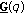 and
and 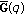 are continuous at
are continuous at 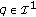 in the
in the 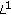 topology
topology  or even in the weak topology
or even in the weak topology  . See Lemmas 2.4 and 2.5.
. See Lemmas 2.4 and 2.5.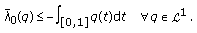
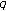 for which
for which 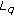 admits AMP, while (4.70) is violated. For example, let
admits AMP, while (4.70) is violated. For example, let 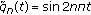 and
and 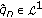 be defined by
be defined by 
 of (2.1) are
of (2.1) are 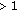 (
(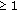 , resp.). However, for those potentials as in Theorem 1.1, zeros of solutions of (2.1) may not be so evenly distributed. This is the difference between the sufficient conditions in this subsection and our optimal conditions given in Theorem 1.1.
, resp.). However, for those potentials as in Theorem 1.1, zeros of solutions of (2.1) may not be so evenly distributed. This is the difference between the sufficient conditions in this subsection and our optimal conditions given in Theorem 1.1. -Laplacian with periodic potentials. Journal of the London Mathematical Society. Second Series 2001,64(1):125-143. 10.1017/S0024610701002277
-Laplacian with periodic potentials. Journal of the London Mathematical Society. Second Series 2001,64(1):125-143. 10.1017/S0024610701002277 topology. preprint
topology. preprint norms. Proceedings of the American Mathematical Society 2002,130(11):3325-3333. 10.1090/S0002-9939-02-06462-6
norms. Proceedings of the American Mathematical Society 2002,130(11):3325-3333. 10.1090/S0002-9939-02-06462-6 -Laplacian with sign-changing potential. Nonlinear Analysis: Theory, Methods & Applications 2010,72(7-8):3436-3446. 10.1016/j.na.2009.12.028
-Laplacian with sign-changing potential. Nonlinear Analysis: Theory, Methods & Applications 2010,72(7-8):3436-3446. 10.1016/j.na.2009.12.028 -Laplacian to be non-degenerate. Mathematische Nachrichten 2005,278(15):1823-1836. 10.1002/mana.200410342
-Laplacian to be non-degenerate. Mathematische Nachrichten 2005,278(15):1823-1836. 10.1002/mana.200410342