- Research Article
- Open access
- Published:
Existence and Nonexistence of Positive Solutions for Singular 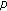 -Laplacian Equation in
-Laplacian Equation in 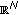
Boundary Value Problems volume 2010, Article number: 607453 (2010)
Abstract
We study the existence and nonexistence of solutions for the singular quasilinear problem  ,
,  ,
,  ,
,  ,
,  , where
, where  ,
,  and
and  behave like
behave like  and
and  with
with  at the origin. We obtain the existence by the upper and lower solution method and the nonexistence by the test function method.
at the origin. We obtain the existence by the upper and lower solution method and the nonexistence by the test function method.
1. Introduction
In this paper, we study through the upper and lower solution method and the test function method the existence and nonexistence of solution to the singular quasilinear elliptic problem

with  ,
,  ,
,  .
.  are the locally Hölder continuous functions, not identically zero and
are the locally Hölder continuous functions, not identically zero and  ) and
) and  are locally Lipschitz continuous functions.
are locally Lipschitz continuous functions.
The study of this type of equation in (1.1) is motivated by its various applications, for instance, in fluid mechanics, in Newtonian fluids, in flow through porous media, and in glaciology; see [1]. The equation in (1.1) involves singularities not only in the nonlinearities but also in the differential operator.
Many authors studied this kind of problem for the case  ; see [2–7]. In these works, the nonlinearities have sublinear and suplinear growth at infinity, and they behave like a function
; see [2–7]. In these works, the nonlinearities have sublinear and suplinear growth at infinity, and they behave like a function  (
( , or
, or  ) at the origin. Roughly speaking, in this case we say that the nonlinearities are concave and convex or "slow diffusion and fast diffusion''; see [8].
) at the origin. Roughly speaking, in this case we say that the nonlinearities are concave and convex or "slow diffusion and fast diffusion''; see [8].
When  ,
,  , and
, and  ,
,  , by using the lower and upper solution method, Santos in [5] finds a real number
, by using the lower and upper solution method, Santos in [5] finds a real number  , such that the problem (1.1) has at least one solution if
, such that the problem (1.1) has at least one solution if  .
.
For  , the existence and multiplicity of solution of singular elliptic equation like (1.1) in a bounded domain
, the existence and multiplicity of solution of singular elliptic equation like (1.1) in a bounded domain  with the zero Dirichlet data have been widely studied by many authors, for example, the authors [9–13] and references therein. Assunção et al. in [14] studied the multiplicity of solution for the singular equations in (1.1) with
with the zero Dirichlet data have been widely studied by many authors, for example, the authors [9–13] and references therein. Assunção et al. in [14] studied the multiplicity of solution for the singular equations in (1.1) with  ,
,  ,
,  , and
, and  in
in  . Similar consideration can be found in [15–20] and references therein. We note that the variation method is widely used in the above references.
. Similar consideration can be found in [15–20] and references therein. We note that the variation method is widely used in the above references.
Recently, Chen et al. in [21, 22], by using a variational approach, got some existence of solution for (1.1) with  and
and  ,
,  . For the case
. For the case  ,
,  , the problem for the existence of solution for (1.1) is still open. It seems difficult to consider the case
, the problem for the existence of solution for (1.1) is still open. It seems difficult to consider the case  by variational method.
by variational method.
The main aim of this work is to study the existence and nonexistence of solution for (1.1), where  is sublinear and
is sublinear and  is suplinear. We will use the upper and lower solution method. To the best of our knowledge, there is little information on upper and lower solution method for the problem (1.1). So it is necessary to establish this technique in unbounded domain. To obtain the existence, the assumption
is suplinear. We will use the upper and lower solution method. To the best of our knowledge, there is little information on upper and lower solution method for the problem (1.1). So it is necessary to establish this technique in unbounded domain. To obtain the existence, the assumption  (see (2.17) below) is essential. By this, an upper solution for (1.1) is obtained.
(see (2.17) below) is essential. By this, an upper solution for (1.1) is obtained.
We also obtain a sufficient condition on  ,
,  to guarantee the nonexistence of nontrivial solution for the problem (2.21). (see Theorem 2.5 below). It must be particularly pointed out that our primary interest is in the mixed case in which
to guarantee the nonexistence of nontrivial solution for the problem (2.21). (see Theorem 2.5 below). It must be particularly pointed out that our primary interest is in the mixed case in which  with
with  satisfying
satisfying

while  satisfies
satisfies

This paper is organized as follows. In Section 2, we state the main results and present some preliminaries which will be used in what follows. We also introduce the precise hypotheses under which our problem is studied. In Section 3, we give the proof of some lemmas and the existence. The proof of nonexistence is given in Section 4.
2. Preliminaries and Main Results
Let us now introduce some weighted Sobolev spaces and their norms. Let  be a bounded domain in
be a bounded domain in  with smooth boundary
with smooth boundary  . If
. If  and
and  , we define
, we define  as being the subspace of
as being the subspace of  of the Lebesgue measurable function
of the Lebesgue measurable function  , satisfying
, satisfying

If  and
and  , we define
, we define  (resp.,
(resp.,  as being the closure of
as being the closure of  (resp.,
(resp.,  ) with respect to the norm defined by
) with respect to the norm defined by

For the weighted Sobolev space  , we have the following compact imbedding theorem which is an extension of the classical Rellich-Kondrachov compact theorem.
, we have the following compact imbedding theorem which is an extension of the classical Rellich-Kondrachov compact theorem.
Theorem 2.1 ((compact imbedding theorem) [13]).
Suppose that  is an open bounded domain with
is an open bounded domain with  boundary and
boundary and  ,
,  ,
,  . Then, the imbedding
. Then, the imbedding  is compact if
is compact if  ,
,  .
.
We now consider the existence of positive solutions for problem (1.1). Our main tool will be the upper and lower solution method. This method, in the bounded domain situation, has been used by many authors, for instance, [10, 12, 13]. But for the unbounded domain, we need to establish this method and then to construct an upper solution and a lower solution for (1.1). We now give the definitions of upper and lower solutions.
Definition 2.2 (see [10, 12]).
A function  is said to be a weak lower solution of the equation
is said to be a weak lower solution of the equation

if

or

for any  ,
,  .
.
Similarly, a function  is said to be a weak upper solution of (2.3) if
is said to be a weak upper solution of (2.3) if

or

for any  and
and  in
in  .
.
A function  is said to be a weak solution of (2.3) if and only if
is said to be a weak solution of (2.3) if and only if  is a weak lower solution and weak upper solution of (2.3).
is a weak lower solution and weak upper solution of (2.3).
A function  is said to be less than or equal to
is said to be less than or equal to  on
on  if
if  .
.
If  and
and  , we define the weighted Sobolev space
, we define the weighted Sobolev space  as being the closure of
as being the closure of  with respect to the norm
with respect to the norm  defined by
defined by

The following lemma will be basic in our approach.
Lemma 2.3.
Let  be Lipschitz continuous and nondecreasing in
be Lipschitz continuous and nondecreasing in  and locally Hölder continuous in
and locally Hölder continuous in  . Moreover, assume that there exist the functions
. Moreover, assume that there exist the functions  such that
such that

Then, there exist a minimal weak solution  and a maximal weak solution
and a maximal weak solution  of (2.3) satisfying
of (2.3) satisfying

and  .
.
Proof.
Denote  ,
,  . Let
. Let  be a pair of upper and lower solutions of (2.3) with
be a pair of upper and lower solutions of (2.3) with  , a.e. in
, a.e. in  . We consider the boundary value problem
. We consider the boundary value problem

By Theorem 1.1 in [10], one concludes that there exists  which is a weak solution of (2.11) with
which is a weak solution of (2.11) with  a.e. in
a.e. in  for
for  .
.
We define its extension by

Similarly, let  be a weak solution of the boundary value problem
be a weak solution of the boundary value problem

and its extension is defined by

Since  , we have
, we have  . By Theorem 2.4 in [12], we have
. By Theorem 2.4 in [12], we have

for  . In view of (2.15), the pointwise limits
. In view of (2.15), the pointwise limits

exist and  in
in  .
.
Similar to the proof Theorem 1.1 in [10] and the proof of Theorem 7.5.1 in [23], it is not difficult to get from Theorem 2.1 that  is the maximal weak solution and
is the maximal weak solution and  the minimal solution of (2.3), which satisfies (2.10) and
the minimal solution of (2.3), which satisfies (2.10) and  . This ends the proof of Lemma 2.3.
. This ends the proof of Lemma 2.3.
Our main results read as follows.
Theorem 2.4 (existence).
Let  ,
,  . Assume the following.
. Assume the following.
The nonnegative functions  are Lipschitz continuous and nondecreasing,
are Lipschitz continuous and nondecreasing,  . Additionally,
. Additionally,  and
and  with
with  .
.
The nonnegative functions  ,
,  are locally Hölder continuous. Let
are locally Hölder continuous. Let  . If
. If

then there exists  , such that
, such that  , and the problem (1.1) admits a weak solution
, and the problem (1.1) admits a weak solution  .
.
Theorem 2.5 (nonexistence).
Let  ,
,  . Assume that
. Assume that
 ;
;
there exist  such that
such that

the functions  in
in  satisfy
satisfy

where  and
and

Then the problem

has no nontrivial solution  .
.
Remark 2.6.
If assumption (2.19) holds, then

with  ,
,  .
.
In fact, for this case, there exist  and
and  such that
such that

for  . Therefore,
. Therefore,

So, condition (2.19) implies (2.22).
3. Proof of Existence
Before proofing the existence, we present some preliminary lemmas which will be useful in what follows.
Lemma 3.1.
Suppose that  ,
,  is local Hölder continuous and satisfies
is local Hölder continuous and satisfies

Then the problem

has a weak solution  , where
, where  .
.
Proof.
Let  . Then
. Then  . Denote
. Denote

Obviously,  and
and  . It is easy to verify that
. It is easy to verify that

This shows that  (resp.,
(resp.,  ) is a lower (resp., upper) solution of (3.2). Then by Lemma 2.3, there exists a weak solution
) is a lower (resp., upper) solution of (3.2). Then by Lemma 2.3, there exists a weak solution  for problem (3.2) satisfying
for problem (3.2) satisfying  , and
, and

Lemma 3.2.
Let  . If
. If
-
(1)
 (3.6)
(3.6)
-
(2)
 (3.7)
(3.7)
one has  .
.
Proof.
-
(1)
Since
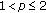 ,
,  . By the Hölder inequality, we obtain
. By the Hölder inequality, we obtain  (3.8)
(3.8)
-
(2)
If
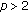 and
and 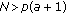 , we take
, we take 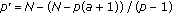 and then
and then 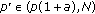 .
.
Note that

This implies  and ends the proof of Lemma 3.2.
and ends the proof of Lemma 3.2.
Corollary 3.3.
If  satisfies the conditions in Lemma 3.2, then the problem (3.2) admits a solution
satisfies the conditions in Lemma 3.2, then the problem (3.2) admits a solution  .
.
Lemma 3.4.
Suppose that  is nondecreasing and
is nondecreasing and  with
with  . Additionally, let the function
. Additionally, let the function  be locally Hölder continuous and satisfy
be locally Hölder continuous and satisfy

where  . Then the problem
. Then the problem

has a weak solution  .
.
Proof.
We first consider the problem

By Lemma 3.1, there is a solution  for (3.12) satisfying
for (3.12) satisfying  . In order to get the existence of solution for (3.11), we chose a pair of upper-lower solution of the equation in (3.11) by means of
. In order to get the existence of solution for (3.11), we chose a pair of upper-lower solution of the equation in (3.11) by means of  .
.
Let  . It is easy to verify that
. It is easy to verify that  is an upper solution of
is an upper solution of

if and only if

or

By the assumption on  , we know that there exists
, we know that there exists  , such that
, such that  . So,
. So,  . Then we take
. Then we take  so that
so that  is an upper solution of (3.13).
is an upper solution of (3.13).
We now construct a lower solution of (3.13). Consider the boundary value problem

for  .
.
By Theorem 3.1 in [12], there exists a solution  for (3.16). We define an extension by
for (3.16). We define an extension by  for
for  . Then, by Theorem 2.4 in [12] and Díaz-Saá's inequality in [24], we get
. Then, by Theorem 2.4 in [12] and Díaz-Saá's inequality in [24], we get

Setting  and performing some standard computations, we see that
and performing some standard computations, we see that  ,
,

and  in
in  . Then, our result follows from Lemma 2.3.
. Then, our result follows from Lemma 2.3.
We now give the proof of Theorem 2.4.
Proof of Theorem 2.4.
Let  be a solution of the problem
be a solution of the problem

where  . We see that
. We see that  is an upper solution of the equation
is an upper solution of the equation

if and only if

or

Since

we have a constant  , such that
, such that

Denote

Since  , we have
, we have  ,
,  and there exist
and there exist  , such that
, such that  for
for  and
and  for
for  . Then
. Then  . A simple computation shows that
. A simple computation shows that

Thus

Hence, for any  , there exists a unique
, there exists a unique  , such that
, such that  . That is
. That is

Now defining  , we get
, we get

This shows that  is an upper solution of (3.20). Noting that
is an upper solution of (3.20). Noting that

we know that  is an upper solution of (1.1). Let
is an upper solution of (1.1). Let  be a solution of (3.11). Obviously,
be a solution of (3.11). Obviously,  is a lower solution of (1.1). We now show that
is a lower solution of (1.1). We now show that  in
in  .
.
Since  for
for  and
and  as
as  , then for any
, then for any  , there exist
, there exist  , such that
, such that  . Without loss of generality, let
. Without loss of generality, let  .
.
From the proof of Lemma 3.4 and the definition of  , we have
, we have  for
for  . Further, by (3.17), we get
. Further, by (3.17), we get  . Letting
. Letting  , we obtain
, we obtain  in
in  .
.
By Lemma 2.3, there exists a solution  for the problem (1.1). We then complete the proof of Theorem 2.4.
for the problem (1.1). We then complete the proof of Theorem 2.4.
Remark 3.5.
The nonlinear term  can be regarded as a perturbation of the nonlinear term
can be regarded as a perturbation of the nonlinear term  .
.
4. Proof of Nonexistence
In order to prove the nonexistence of nontrivial solution of the problem (2.21), we use the test function method, which has been used in [25] and references therein. Some modification has been made in our proof. The proof is based on argument by contradiction which involves a priori estimate for a nonnegative solution of (2.21) by carefully choosing the special test function and scaling argument.
Proof of Theorem 2.5.
Let  be defined by
be defined by

and put  , by which the parameters
, by which the parameters  will be determined later. It is not difficult to verify that
will be determined later. It is not difficult to verify that  and
and  , where
, where  .
.
Suppose that  is a solution to problem (2.21). Without loss of generality, we can assume that
is a solution to problem (2.21). Without loss of generality, we can assume that  in
in  (otherwise, we consider
(otherwise, we consider  and let
and let 
 ). Let
). Let  be a parameter (
be a parameter ( will also be chosen below).
will also be chosen below).
By the Young inequality, we get

where  ,
,  , and
, and  satisfy (2.18) and
satisfy (2.18) and  ,
,  .
.
Multiplying the equation in (2.21) by  and integrating by parts, we obtain
and integrating by parts, we obtain

Then applying the Young inequality with parameter  , we have
, we have

where  .
.
Similarly, let us multiply the equation in (2.21) by  and integrate by parts:
and integrate by parts:

By (4.4),

Now, we apply the Hölder inequality to the integral on the right-hand side of (4.6):

with  ,
,  and
and  .
.
Since  , we chose
, we chose  so small that
so small that  . Then, we have
. Then, we have

with  ,
,  .
.
Since  ,
,  with
with  . Then we get
. Then we get

where  and
and  .
.
Let  . Then,
. Then,

Similarly,

Then it follows from (4.5)–(4.11) that

with  and
and

If  , it follows from (4.12) that
, it follows from (4.12) that

This implies that  , a.e. in
, a.e. in  . That is,
. That is,  is a trivial solution for (2.21).
is a trivial solution for (2.21).
If  , then (4.12) gives that
, then (4.12) gives that

By (4.5), we derive

Reasoning as in the first part of the proof, we infer that

Letting  in (4.17), we obtain (4.14). Thus,
in (4.17), we obtain (4.14). Thus,  , a.e. in
, a.e. in  . Then the proof of Theorem 2.5 is completed.
. Then the proof of Theorem 2.5 is completed.
References
Cîrstea F, Motreanu D, Rădulescu V: Weak solutions of quasilinear problems with nonlinear boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2001,43(5):623-636. 10.1016/S0362-546X(99)00224-2
Goncalves JV, Santos CA: Existence and asymptotic behavior of non-radially symmetric ground states of semilinear singular elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(4):719-727. 10.1016/j.na.2005.09.036
Mohammed A: Ground state solutions for singular semi-linear elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2009,71(3-4):1276-1280. 10.1016/j.na.2008.11.080
Noussair ES, Swanson CA, Yang JF: Quasilinear elliptic problems with critical exponents. Nonlinear Analysis: Theory, Methods & Applications 1993,20(3):285-301. 10.1016/0362-546X(93)90164-N
Santos CA: Non-existence and existence of entire solutions for a quasi-linear problem with singular and super-linear terms. Nonlinear Analysis: Theory, Methods & Applications 2010,72(9-10):3813-3819. 10.1016/j.na.2010.01.017
Santos CA: On ground state solutions for singular and semi-linear problems including super-linear terms at infinity. Nonlinear Analysis: Theory, Methods & Applications 2010,71(12):6038-6043.
Santos CA: Entire solutions for a quasilinear problem in the presence of sublinear and super-linear terms. Boundary Value Problems 2009, -16.
Cañada A, Drábek P, Gámez JL: Existence of positive solutions for some problems with nonlinear diffusion. Transactions of the American Mathematical Society 1997,349(10):4231-4249. 10.1090/S0002-9947-97-01947-8
Assunção RB, Carrião PC, Miyagaki OH: Subcritical perturbations of a singular quasilinear elliptic equation involving the critical Hardy-Sobolev exponent. Nonlinear Analysis: Theory, Methods & Applications 2007,66(6):1351-1364. 10.1016/j.na.2006.01.027
Brock F, Iturriaga L, Sánchez J, Ubilla P:Existence of positive solutions for
 -Laplacian problems with weights. Communications on Pure and Applied Analysis 2006,5(4):941-952.
-Laplacian problems with weights. Communications on Pure and Applied Analysis 2006,5(4):941-952.Kristály A, Varga C: Multiple solutions for a degenerate elliptic equation involving sublinear terms at infinity. Journal of Mathematical Analysis and Applications 2009,352(1):139-148. 10.1016/j.jmaa.2008.03.025
Miyagaki OH, Rodrigues RS: On positive solutions for a class of singular quasilinear elliptic systems. Journal of Mathematical Analysis and Applications 2007,334(2):818-833. 10.1016/j.jmaa.2007.01.018
Xuan B: The solvability of quasilinear Brezis-Nirenberg-type problems with singular weights. Nonlinear Analysis: Theory, Methods & Applications 2005,62(4):703-725. 10.1016/j.na.2005.03.095
Assunção RB, Carrião PC, Miyagaki OH: Multiplicity of solutions for critical singular problems. Applied Mathematics Letters 2006,19(8):741-746. 10.1016/j.aml.2005.10.004
Calzolari E, Filippucci R, Pucci P:Existence of radial solutions for the
 -Laplacian elliptic equations with weights. Discrete and Continuous Dynamical Systems A 2006,15(2):447-479.
-Laplacian elliptic equations with weights. Discrete and Continuous Dynamical Systems A 2006,15(2):447-479.Clément P, Manásevich R, Mitidieri E: Some existence and non-existence results for a homogeneous quasilinear problem. Asymptotic Analysis 1998,17(1):13-29.
García-Huidobro M, Manásevich R, Yarur CS:On the structure of positive radial solutions to an equation containing a
 -Laplacian with weight. Journal of Differential Equations 2006,223(1):51-95. 10.1016/j.jde.2005.04.012
-Laplacian with weight. Journal of Differential Equations 2006,223(1):51-95. 10.1016/j.jde.2005.04.012Pucci P, García-Huidobro M, Manásevich R, Serrin J: Qualitative properties of ground states for singular elliptic equations with weights. Annali di Matematica Pura ed Applicata 2006,185(4):205-243.
Pucci P, Servadei R:Existence, non-existence and regularity of radial ground states for
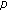 -Laplacain equations with singular weights. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2008,25(3):505-537.
-Laplacain equations with singular weights. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2008,25(3):505-537.Yang Z: Existence of positive entire solutions for singular and non-singular quasi-linear elliptic equation. Journal of Computational and Applied Mathematics 2006,197(2):355-364. 10.1016/j.cam.2005.08.027
Chen C, Wang H:Ground state solutions for singular
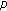 -Laplacian equation in
-Laplacian equation in  . Journal of Mathematical Analysis and Applications 2009,351(2):773-780. 10.1016/j.jmaa.2008.11.010
. Journal of Mathematical Analysis and Applications 2009,351(2):773-780. 10.1016/j.jmaa.2008.11.010Wu H, Chen C:Decaying solution for singular
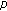 -Laplacian equation. Applied Mathematics and Computation 2008,204(2):833-838. 10.1016/j.amc.2008.07.030
-Laplacian equation. Applied Mathematics and Computation 2008,204(2):833-838. 10.1016/j.amc.2008.07.030Pao CV: Nonlinear Parabolic and Elliptic Equations. Plenum, New York, NY, USA; 1992:xvi+777.
Díaz JI, Saá JE: Existence et unicité de solutions positives pour certaines équations elliptiques quasilinéaires. Comptes Rendus des Séances de l'Académie des Sciences 1987,305(12):521-524.
Mitidieri È, Pokhozhaev SI: A priori estimates and the absence of solutions of nonlinear partial differential equations and inequalities. Trudy Matematicheskogo Instituta Imeni V. A. Steklova 2001, 234: 1-384. translation in Proceedings of the Steklov Institute of Mathematics, 234, no. 3, 1–362, 2001
Acknowledgments
The authors wish to express their gratitude to the referees for useful comments and suggestions. The work was supported by the Fundamental Research Funds for the Central Universities (Grant no. 2010B17914) and Science Funds of Hohai University (Grants no. 2008430211 and 2008408306).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, C., Wang, Z. & Wang, F. Existence and Nonexistence of Positive Solutions for Singular 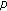 -Laplacian Equation in
-Laplacian Equation in 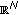 .
Bound Value Probl 2010, 607453 (2010). https://doi.org/10.1155/2010/607453
.
Bound Value Probl 2010, 607453 (2010). https://doi.org/10.1155/2010/607453
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/607453


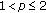 ,
,  . By the Hölder inequality, we obtain
. By the Hölder inequality, we obtain 
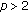 and
and 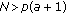 , we take
, we take 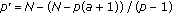 and then
and then 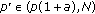 .
. -Laplacian problems with weights. Communications on Pure and Applied Analysis 2006,5(4):941-952.
-Laplacian problems with weights. Communications on Pure and Applied Analysis 2006,5(4):941-952. -Laplacian elliptic equations with weights. Discrete and Continuous Dynamical Systems A 2006,15(2):447-479.
-Laplacian elliptic equations with weights. Discrete and Continuous Dynamical Systems A 2006,15(2):447-479. -Laplacian with weight. Journal of Differential Equations 2006,223(1):51-95. 10.1016/j.jde.2005.04.012
-Laplacian with weight. Journal of Differential Equations 2006,223(1):51-95. 10.1016/j.jde.2005.04.012 -Laplacain equations with singular weights. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2008,25(3):505-537.
-Laplacain equations with singular weights. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 2008,25(3):505-537. -Laplacian equation in
-Laplacian equation in  . Journal of Mathematical Analysis and Applications 2009,351(2):773-780. 10.1016/j.jmaa.2008.11.010
. Journal of Mathematical Analysis and Applications 2009,351(2):773-780. 10.1016/j.jmaa.2008.11.010 -Laplacian equation. Applied Mathematics and Computation 2008,204(2):833-838. 10.1016/j.amc.2008.07.030
-Laplacian equation. Applied Mathematics and Computation 2008,204(2):833-838. 10.1016/j.amc.2008.07.030