- Research Article
- Open access
- Published:
Quenching for a Reaction-Diffusion System with Coupled Inner Singular Absorption Terms
Boundary Value Problems volume 2010, Article number: 797182 (2010)
Abstract
we devote to investigate the quenching phenomenon for a reaction-diffusion system with coupled singular absorption terms,  ,
,  . The solutions of the system quenches in finite time for any initial data are obtained, and the blow-up of time derivatives at the quenching point is verified. Moreover, under appropriate hypotheses, the criteria to identify the simultaneous and nonsimultaneous quenching are found, and the four kinds of quenching rates for different nonlinear exponent regions are given. Finally, some numerical experiments are performed, which illustrate our results.
. The solutions of the system quenches in finite time for any initial data are obtained, and the blow-up of time derivatives at the quenching point is verified. Moreover, under appropriate hypotheses, the criteria to identify the simultaneous and nonsimultaneous quenching are found, and the four kinds of quenching rates for different nonlinear exponent regions are given. Finally, some numerical experiments are performed, which illustrate our results.
1. Introduction
This paper deals with the following nonlinear parabolic equations with null Neumann boundary conditions:

where  for
for  ,
,  is a bounded domain with smooth boundary, the initial data
is a bounded domain with smooth boundary, the initial data  and
and  are positive, smooth, and compatible with the boundary data.
are positive, smooth, and compatible with the boundary data.
Because of the singular nonlinearity inner absorption terms of (1.1), the so-called finite-time quenching may occur for the model. We say that the solution  of the problem (1.1) quenches, if there exists a time
of the problem (1.1) quenches, if there exists a time  (
(  denotes the quenching time,
denotes the quenching time,  denotes quenching point), such that
denotes quenching point), such that

For a quenching solution  of (1.1), the inf norm of one of the components must tend to
of (1.1), the inf norm of one of the components must tend to  as
as  tends to the quenching time
tends to the quenching time  . The case when
. The case when  quenches and
quenches and  remains bounded from zero is called non-simultaneous quenching. We will call the case, when both components
remains bounded from zero is called non-simultaneous quenching. We will call the case, when both components  and
and  quench at the same time, as simultaneous quenching. The purpose of this paper is to find a criteria to identify simultaneous and non-simultaneous quenching for (1.1) and then establish quenching rates for the different cases.
quench at the same time, as simultaneous quenching. The purpose of this paper is to find a criteria to identify simultaneous and non-simultaneous quenching for (1.1) and then establish quenching rates for the different cases.
In order to motivate the main results for system (1.1), we recall some classical results for the related system. de Pablo et al., firstly distinguished non-simultaneous quenching from simultaneous one in [1]. They considered a heat system coupled via inner absorptions as follows:

Recently, Zheng and Wang deduced problem (1.3) to  -dimensional with positive Dirichlet boundary condition in [2]. Then, Zhou et al. have given a natural continuation for problem (1.3) beyond quenching time
-dimensional with positive Dirichlet boundary condition in [2]. Then, Zhou et al. have given a natural continuation for problem (1.3) beyond quenching time  for the case of non-simultaneous quenching in [3].
for the case of non-simultaneous quenching in [3].
Replacing the coupled inner absorptions in (1.1) by the coupled boundary fluxes, one gets

Recently, the simultaneous and non-simultaneous quenching for problem (1.4), and what is related to it, was studied by many authors (see [4–7] and references therein).
In order to investigate the problem (1.1), it is necessary to recall the blow-up problem of the following reaction-diffusion system:

with positive powers  has been extensively studied by many authors for various problems such as global existence and finite time blow-up, Fujita exponents, non-simultaneous and simultaneous blow-up, and blow-up rates, (see [8–10] and references therein). However, unlike the blow-up problem, there are less papers consider the weakly coupled quenching problem like (1.1), differently from the generally considered, there are two additional singular factors, namely,
has been extensively studied by many authors for various problems such as global existence and finite time blow-up, Fujita exponents, non-simultaneous and simultaneous blow-up, and blow-up rates, (see [8–10] and references therein). However, unlike the blow-up problem, there are less papers consider the weakly coupled quenching problem like (1.1), differently from the generally considered, there are two additional singular factors, namely,  and
and  for the inner absorptions of
for the inner absorptions of  and
and  , respectively. In this paper, we will show real contributions of the two additional singular factors to the quenching behavior of solutions. Our main results are stated as follows.
, respectively. In this paper, we will show real contributions of the two additional singular factors to the quenching behavior of solutions. Our main results are stated as follows.
Theorem 1.1.
If  and
and  , then the solution of the system (1.1) quenches in finite time for every initial data.
, then the solution of the system (1.1) quenches in finite time for every initial data.
On the other hand, some authors understand quenching as blow-up of time derivatives while the solution itself remains bounded (see [11–13]). In present paper, we assume that the initial data satisfy

Theorem 1.2.
Let  and the radial initial function satisfies (1.6), then
and the radial initial function satisfies (1.6), then  blows up in finite time.
blows up in finite time.
Next, we characterize the ranges of parameters to distinguish simultaneous and non-simultaneous quenching. In order to simplify our work, we deal with the radial solutions of (1.1) with  , and the radial increasing initial data satisfies (1.6). Thus we, see that
, and the radial increasing initial data satisfies (1.6). Thus we, see that  is the only quenching point (see [2, 14]). Without loss of generality, we only consider the non-simultaneous quenching with
is the only quenching point (see [2, 14]). Without loss of generality, we only consider the non-simultaneous quenching with  remaining strictly positive, and our main results are stated as follows.
remaining strictly positive, and our main results are stated as follows.
Theorem 1.3.
If  and
and  , then any quenching in (1.1) must be simultaneous.
, then any quenching in (1.1) must be simultaneous.
Theorem 1.4.
If  and
and  , then any quenching in (1.1) is non-simultaneous with
, then any quenching in (1.1) is non-simultaneous with  being strictly positive.
being strictly positive.
Theorem 1.5.
If  and
and  , then both simultaneous and non-simultaneous quenching may occur in (1.1) depending on the initial data.
, then both simultaneous and non-simultaneous quenching may occur in (1.1) depending on the initial data.
Remark 1.6.
In particular, if we choose  , then we obtain that the ranges of parameters to distinguish simultaneous and non-simultaneous quenching coincide with the problem (1.3) (see [1, 2]). Moreover, this criteria to identify the simultaneous and non-simultaneous quenching is the same with the problem (1.4) which coupled boundary fluxes (see [6]). This situation also happens for the blow-up problem (see [8, 10, 15]).
, then we obtain that the ranges of parameters to distinguish simultaneous and non-simultaneous quenching coincide with the problem (1.3) (see [1, 2]). Moreover, this criteria to identify the simultaneous and non-simultaneous quenching is the same with the problem (1.4) which coupled boundary fluxes (see [6]). This situation also happens for the blow-up problem (see [8, 10, 15]).
Next, we deal with quenching rates. To state our results more conveniently, we introduce the notation  which means that there exist two finite positive constants
which means that there exist two finite positive constants  such that
such that  , and the two parameters
, and the two parameters  and
and  verifying
verifying

or equivalently,

In terms of parameters  and
and  , the quenching rates of problem (1.1) can be shown as follow.
, the quenching rates of problem (1.1) can be shown as follow.
Theorem 1.7.
If quenching is non-simultaneous and, for instance,  is the quenching variable, then
is the quenching variable, then  .
.
Theorem 1.8.
If quenching is simultaneous, then for  close to
close to  , we have
, we have
(i) for
for  ,
,  or
or  ;
;
(ii) for
for  and
and  ;
;
(iii) for
for  and
and  .
.
The plan of this paper is organized as follows. In Section 2, we distinguish non-simultaneous quenching from simultaneous one. The four kinds of non-simultaneous and simultaneous quenching rates for different nonlinear exponent regions are given in Section 3. In the Section 4, we perform some numerical experiments which illustrate our results.
2. Simultaneous and Non-Simultaneous Quenching
Proof of Theorem 1.1.
Assume that  is the classical solution of (1.1) with the maximal existence time
is the classical solution of (1.1) with the maximal existence time  . The maximum principle implies
. The maximum principle implies  and
and  in
in  . Let
. Let  . Hence, integrating (1.1) in space and using Green's formula, we have
. Hence, integrating (1.1) in space and using Green's formula, we have

Consequently,

Thus, the solution of the problem (1.1) quenches in finite time. The prove of Theorem 1.1 is complete.
In order to prove Theorem 1.2, we need the following Lemma.
Lemma 2.1.
Assume that  and the radial nondecreasing initial data satisfy (1.6), then there exists a small
and the radial nondecreasing initial data satisfy (1.6), then there exists a small  such that
such that

Proof.
Let  . Thus,
. Thus,

Since  and
and  are radial and nondecreasing in
are radial and nondecreasing in  , we have
, we have  . A similar computation holds for
. A similar computation holds for  , and we obtain
, and we obtain

with boundary conditions

From (1.6), it is easy to deduce  in
in  (see [13, 14]). Choosing
(see [13, 14]). Choosing  small enough, we have that the initial data verifying
small enough, we have that the initial data verifying

Hence, by the comparison result, we derive that

This proves Lemma 2.1.
Proof of Theorem 1.2.
This theorem is the direct result of Theorem 1.1 and Lemma 2.1.
Next, we characterize the ranges of parameters to distinguish simultaneous and non-simultaneous quenching. By the hypothesis on the initial data, we obtain  and
and  for
for  (see [2, 14]). We collect the estimates of the time derivatives obtained before. Clearly, the only quenching point is
(see [2, 14]). We collect the estimates of the time derivatives obtained before. Clearly, the only quenching point is  (see [2]), we only care for the original point,
(see [2]), we only care for the original point,


Proof of Theorem 1.3.
We argue by contradiction. Assume that there exists  such that
such that  on
on  and
and  quenching at the time
quenching at the time  . Through (2.10), we have
. Through (2.10), we have  , integrating from
, integrating from  to
to  we get
we get  . Together with (2.9) we have
. Together with (2.9) we have  . Integrating in
. Integrating in  , we obtain
, we obtain

If  , we have the left hand of the above inequality diverged. So, we get a contradiction. The proof of Theorem 1.3 is finished.
, we have the left hand of the above inequality diverged. So, we get a contradiction. The proof of Theorem 1.3 is finished.
Proof of Theorem 1.4.
First, assume that  and
and  . Combining (2.9) with (2.10), we get
. Combining (2.9) with (2.10), we get

Since  , integrating the first inequality in the (2.12) from
, integrating the first inequality in the (2.12) from  to
to  , we have
, we have

where  are positive constants, the above inequality requires that
are positive constants, the above inequality requires that  remains positive up to the quenching time. The case
remains positive up to the quenching time. The case  can be treated in an analogous way. The proof of Theorem 1.4 is complete.
can be treated in an analogous way. The proof of Theorem 1.4 is complete.
Proof of Theorem 1.5.
If  and the initial data
and the initial data  on
on  , thus, it is easy to see that for problem (1.1) simultaneous quenching occurs.
, thus, it is easy to see that for problem (1.1) simultaneous quenching occurs.
On the other hand, we want to choose  small in order that the quenching time
small in order that the quenching time  (through Theorem 1.1, we get
(through Theorem 1.1, we get  ) be so small that
) be so small that  does not have time to vanish.
does not have time to vanish.
Let  be fixed. From
be fixed. From  in
in  , we obtain
, we obtain

Together with the estimate (2.12), we get

Integrating in  , we obtain
, we obtain

It is easy to see that the last term of the above inequality is strictly positive, if  is small enough and
is small enough and  , therefore, we prove that under the condition
, therefore, we prove that under the condition  and
and  , for the solution of (1.1) non-simultaneous quenching may occur. The proof of Theorem 1.5 is complete.
, for the solution of (1.1) non-simultaneous quenching may occur. The proof of Theorem 1.5 is complete.
3. Quenching Rates
In this section, we deal with the all possible quenching rates in model (1.1).
Proof of Theorem 1.7.
Under the condition of Theorem 1.7, it holds that  . By (2.10), we have
. By (2.10), we have

Thus,

The proof of Theorem 1.7 is complete.
Proof of Theorem 1.8.
-
(i)
Assume that the quenching of problem (1.1) is simultaneous with
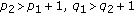 , integrating (2.12) yields
, integrating (2.12) yields  (3.3)
(3.3)
where  . Since we assume that
. Since we assume that  quench at
quench at  , we have
, we have  as
as  .
.
On the other hand, from  and
and  , we get, a positive constant
, we get, a positive constant  such that
such that

Similarly, we can show that there exists a positive constant  such that
such that

Consequently,

Recalling the estimates (2.9) and (2.10), we obtain

Integrating from  to
to  , we get
, we get

If  and
and  , we deduce the quenching rate by a bootstrap argument. First, by (2.9), we get
, we deduce the quenching rate by a bootstrap argument. First, by (2.9), we get  , it follows that
, it follows that  . Employing (2.10), we get
. Employing (2.10), we get  , that is,
, that is,  . Repeating this procedure, we obtain
. Repeating this procedure, we obtain  ,
,  , where
, where  satisfy
satisfy

One can check that  (
( define by (1.8)), and the all positive constants
define by (1.8)), and the all positive constants  are bounded. Therefore, passing to the limit, we get
are bounded. Therefore, passing to the limit, we get  . The reverse inequalities can be obtained in the same way.
. The reverse inequalities can be obtained in the same way.
-
(ii)
If
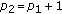 and
and 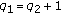 , we have
, we have 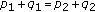 . It is easy to see that
. It is easy to see that  as
as 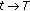 , from (2.9) and (2.10), we obtain
, from (2.9) and (2.10), we obtain 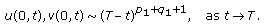 (3.10)
(3.10)
(iii) If  and
and  , from (2.9), we get
, from (2.9), we get

Recalling the estimate (2.10), we get

that is,

Let  , we have
, we have

It is known that the incomplete Gamma function  satisfies
satisfies  for
for  . With
. With  , we obtain
, we obtain

and hence,

Next, we deduce the behaviour for  . Combining with (2.9) and (3.16), we have
. Combining with (2.9) and (3.16), we have

Integrating from  to
to  ,
,

Setting  , we get
, we get

For the incomplete Gamma function  with
with  , we obtain
, we obtain

The proof of Theorem 1.8 is complete.
4. Numerical Experiments
In this section, we perform some numerical experiments, which illustrate our results. Now we introduce the numerical scheme for the space discretization, we discretize applying linear finite elements with mass lumping in a uniform mesh for the space variable and keeping  continuous, it is well known that this discretization in space coincides with the classic central finite difference second-order scheme, (see [16]), Mass lumping is widely used in parabolic problems with blow-up and quenching, (see, e.g., [17, 18]).
continuous, it is well known that this discretization in space coincides with the classic central finite difference second-order scheme, (see [16]), Mass lumping is widely used in parabolic problems with blow-up and quenching, (see, e.g., [17, 18]).
Let us consider the uniform partition of size  of the interval
of the interval  , (
, ( ), and its associated standard piecewise linear finite element space
), and its associated standard piecewise linear finite element space  . The semidiscrete approximation
. The semidiscrete approximation  obtained by the finite element method with mass lumping is defined as
obtained by the finite element method with mass lumping is defined as

where the superindex  denotes the Lagrange interpolation.
denotes the Lagrange interpolation.
We denote with  the values of the numerical approximation at the nodes
the values of the numerical approximation at the nodes  and the time
and the time  . Thus,
. Thus,

where  is the standard base of
is the standard base of  . Then
. Then  satisfies the following ODE system:
satisfies the following ODE system:

where  is the mass matrix obtained with lumping,
is the mass matrix obtained with lumping,  is the stiffness matrix, and
is the stiffness matrix, and  is the Lagrange interpolation of the initial datum
is the Lagrange interpolation of the initial datum  .
.
We take  and
and  . Writing the system (4.3) explicitly, we get the following ODE system:
. Writing the system (4.3) explicitly, we get the following ODE system:

where  and
and  . In order to show the evolution in time of a numerical solution, we chose
. In order to show the evolution in time of a numerical solution, we chose  ,
,  , and
, and  which will be choose later.
which will be choose later.
First, we consider the case  , and the initial data
, and the initial data  , We observe that the solutions of (1.1) quenching only at the origin, if the symmetric initial data with a unique minimum at
, We observe that the solutions of (1.1) quenching only at the origin, if the symmetric initial data with a unique minimum at  (see Figure 1), and the quenching is simultaneous (see Figure 2); If we take
(see Figure 1), and the quenching is simultaneous (see Figure 2); If we take  , and the same initial data (see Figures 3 and 4), then we obtain the results which accords with Theorem 1.3.
, and the same initial data (see Figures 3 and 4), then we obtain the results which accords with Theorem 1.3.
Next, we take  with the same initial data
with the same initial data  . In this case the quenching in (1.1) is non-simultaneous with
. In this case the quenching in (1.1) is non-simultaneous with  being strictly positive (see Figure 5); If we choose
being strictly positive (see Figure 5); If we choose  with the initial data
with the initial data  (see Figure 6), then we can see that our results coincide with Theorem 1.4.
(see Figure 6), then we can see that our results coincide with Theorem 1.4.
Finally, we choose  In Figure 7, we take the initial data
In Figure 7, we take the initial data  , and in Figure 8 we take the different initial data both equal to
, and in Figure 8 we take the different initial data both equal to  , we can see that both non-simultaneous quenching and simultaneous quenching may occur in (1.1), depending on the initial data.
, we can see that both non-simultaneous quenching and simultaneous quenching may occur in (1.1), depending on the initial data.
References
de Pablo A, Quirós F, Rossi JD: Nonsimultaneous quenching. Applied Mathematics Letters 2002,15(3):265-269. 10.1016/S0893-9659(01)00128-8
Zheng S, Wang W: Non-simultaneous versus simultaneous quenching in a coupled nonlinear parabolic system. Nonlinear Analysis: Theory, Methods & Applications 2008,69(7):2274-2285. 10.1016/j.na.2007.08.007
Zhou J, He Y, Mu C: Incomplete quenching of heat equations with absorption. Applicable Analysis 2008,87(5):523-529. 10.1080/00036810802001289
Ferreira R, de Pablo A, Quirós F, Rossi JD: Non-simultaneous quenching in a system of heat equations coupled at the boundary. Zeitschrift für Angewandte Mathematik und Physik 2006,57(4):586-594. 10.1007/s00033-005-0003-z
Ferreira R, de Pablo A, Pérez-Llanos M, Rossi JD: Incomplete quenching in a system of heat equations coupled at the boundary. Journal of Mathematical Analysis and Applications 2008,346(1):145-154. 10.1016/j.jmaa.2008.05.037
Ji R, Zheng S: Quenching behavior of solutions to heat equations with coupled boundary singularities. Applied Mathematics and Computation 2008,206(1):403-412. 10.1016/j.amc.2008.09.018
Zheng S, Song XF: Quenching rates for heat equations with coupled singular nonlinear boundary flux. Science in China. Series A 2008,51(9):1631-1643. 10.1007/s11425-007-0178-1
Escobedo M, Levine HA: Critical blowup and global existence numbers for a weakly coupled system of reaction-diffusion equations. Archive for Rational Mechanics and Analysis 1995,129(1):47-100. 10.1007/BF00375126
Guo J-S, Sasayama S, Wang C-J: Blowup rate estimate for a system of semilinear parabolic equations. Communications on Pure and Applied Analysis 2009,8(2):711-718.
Wang M: Blow-up rate estimates for semilinear parabolic systems. Journal of Differential Equations 2001,170(2):317-324. 10.1006/jdeq.2000.3823
Chan CY: Recent advances in quenching phenomena. Proceedings of Dynamic Systems and Applications, 1996, Atlanta, Ga, USA 2: 107-113.
Kawarada H:On solutions of initial-boundary problem for
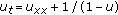 . Publications of the Research Institute for Mathematical Sciences 1975,10(3):729-736.
. Publications of the Research Institute for Mathematical Sciences 1975,10(3):729-736.Salin T: On quenching with logarithmic singularity. Nonlinear Analysis: Theory, Methods & Applications 2003,52(1):261-289. 10.1016/S0362-546X(02)00110-4
Mu C, Zhou S, Liu D: Quenching for a reaction-diffusion system with logarithmic singularity. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5599-5605. 10.1016/j.na.2009.04.055
Pinasco JP, Rossi JD: Simultaneous versus non-simultaneous blow-up. New Zealand Journal of Mathematics 2000,29(1):55-59.
Ciarlet PG: The Finite Element Method for Elliptic Problems, Studies in Mathematics and Its Applications. North-Holland, Amsterdam, The Netherlands; 1978:xix+530.
Ferreira R: Numerical quenching for the semilinear heat equation with a singular absorption. Journal of Computational and Applied Mathematics 2009,228(1):92-103. 10.1016/j.cam.2008.08.041
Groisman P, Quirós F, Rossi JD: Non-simultaneous blow-up in a numerical approximation of a parabolic system. Computational & Applied Mathematics 2002,21(3):813-831.
Acknowledgments
This work is supported in part by NSF of China (10771226) and in part by Innovative Talent Training Project, the Third Stage of "211 Project", Chongqing University, Project no.: S-09110.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhou, S., Mu, C. Quenching for a Reaction-Diffusion System with Coupled Inner Singular Absorption Terms. Bound Value Probl 2010, 797182 (2010). https://doi.org/10.1155/2010/797182
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/797182
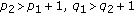 , integrating (2.12) yields
, integrating (2.12) yields 
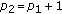 and
and 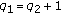 , we have
, we have 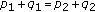 . It is easy to see that
. It is easy to see that  as
as 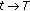 , from (2.9) and (2.10), we obtain
, from (2.9) and (2.10), we obtain 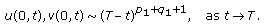

 .
.
 of the solution
of the solution  .
.
 .
.
 of the solution
of the solution  .
.
 of the solution
of the solution  .
.
 of the solution
of the solution  .
.
 of the solution
of the solution  .
.
 of the solution
of the solution  .
. . Publications of the Research Institute for Mathematical Sciences 1975,10(3):729-736.
. Publications of the Research Institute for Mathematical Sciences 1975,10(3):729-736.