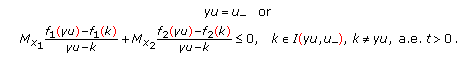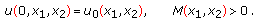- Research Article
- Open access
- Published:
Two-Dimension Riemann Initial-Boundary Value Problem of Scalar Conservation Laws with Curved Boundary
Boundary Value Problems volume 2011, Article number: 138396 (2011)
Abstract
This paper is concerned with the structure of the weak entropy solutions to two-dimension Riemann initial-boundary value problem with curved boundary. Firstly, according to the definition of weak entropy solution in the sense of Bardos-Leroux-Nedelec (1979), the necessary and sufficient condition of the weak entropy solutions with piecewise smooth is given. The boundary entropy condition and its equivalent formula are proposed. Based on Riemann initial value problem, weak entropy solutions of Riemann initial-boundary value problem are constructed, the behaviors of solutions are clarified, and we focus on verifying that the solutions satisfy the boundary entropy condition. For different Riemann initial-boundary value data, there are a total of five different behaviors of weak entropy solutions. Finally, a worked-out specific example is given.
1. Introduction
Multidimensional conservation laws are a famous hard problem that plays an important role in mechanics and physics [1–3]. For Cauchy problem of multi-dimensional scalar conservation laws, Conway and Smoller [4] and Kruzkov [1] have proved that weak solution uniquely exists if it also satisfies entropy condition, and it is called weak entropy solutions. In order to further understand qualitative behavior of solutions, it is also important to investigate multi-dimensional Riemann problems. For two-dimensional case, Lindquist [5], Wagner [6], Zhang and Zheng [7] Guckenheimer [8], Zheng [9] among others, have discussed some relating Riemann problems. In a previous discussion, initial value contains several constant states with discontinuity lines so that self-similar transformations can be applied to reduce two-dimensional problem to one-dimensional case. The situation that initial value contains two constant states divided by a curve can not be solved by selfsimilar transformations, and Yang [10] proposed a new approach for construction of shock wave and rarefaction wave solutions; especially, rarefaction wave was got by constructing implicit function instead of the usual selfsimilar method. This approach can be expanded to general  -dimension. In addition, multi-dimensional scalar conservation laws with boundary are more common in practical problems. Bardos et al. [2] have proved the existence and uniqueness of the weak entropy solution of initial-boundary problems of multi-dimensional scalar conservation laws. The main difficulty for nonlinear conservation laws with boundary is to have a good formation of the boundary condition. Namely, for a fixed initial value, we really can not impose such a condition at the boundary, and the boundary condition is necessarily linked to the entropy condition. Moreover the behavior of solutions for one-dimensional problem with boundary was discussed in [11–18]. However, for multi-dimensional problem with boundary, the behaviors of solutions are still hard to study.
-dimension. In addition, multi-dimensional scalar conservation laws with boundary are more common in practical problems. Bardos et al. [2] have proved the existence and uniqueness of the weak entropy solution of initial-boundary problems of multi-dimensional scalar conservation laws. The main difficulty for nonlinear conservation laws with boundary is to have a good formation of the boundary condition. Namely, for a fixed initial value, we really can not impose such a condition at the boundary, and the boundary condition is necessarily linked to the entropy condition. Moreover the behavior of solutions for one-dimensional problem with boundary was discussed in [11–18]. However, for multi-dimensional problem with boundary, the behaviors of solutions are still hard to study.
In this paper, two-dimensional case as an example of Yang's multi-dimensional Riemann problem [10] is expanded to the case with boundary. Considering two-dimensional Riemann problem for scalar conservation laws with curved boundary,

where  ,
,  and
and  are both constants,
are both constants,  ,
,  ,
,  is a smooth manifold and divides
is a smooth manifold and divides  into two infinite parts,
into two infinite parts,  , and
, and  and denote
and denote  .
.
In Section 2, weak entropy solution of Riemann initial-boundary value problem (1.1) is defined, and the boundary entropy condition is discussed. In Section 3, weak entropy solutions of the corresponding Riemann initial value problem are expressed. In Section 4, using the weak entropy solutions of the corresponding Riemann initial value problem, we construct the weak entropy solutions of Riemann initial-boundary value problem, and prove that they satisfy the boundary entropy condition. The weak entropy solutions include a total of five different shock and rarefaction wave solutions based on different Riemann data. Finally, in Section 5, we give a worked-out specific example.
2. Preliminaries
According to the definition of the weak entropy solution and the boundary entropy condition to the general initial-boundary problems of multi-dimensional scalar conservation laws which was proposed by Bardos et al. [2] and Pan and Lin [13], we can obtain the following definition and three lemmas for Riemann initial-boundary value problem (1.1).
Definition 2.1.
A locally bounded and bounded variation function  on
on  is called a weak entropy solution of Riemann initial-boundary value problem (1.1) if, for any real constant
is called a weak entropy solution of Riemann initial-boundary value problem (1.1) if, for any real constant  and for any nonnegative function
and for any nonnegative function  , it satisfies the following inequality:
, it satisfies the following inequality:

where  is the outward normal vector of curve
is the outward normal vector of curve  .
.
Lemma 2.2.
If  is a weak entropy solution of (1.1), then it satisfies the following boundary: entropy condition
is a weak entropy solution of (1.1), then it satisfies the following boundary: entropy condition

where .
.
It can be easily proved that  ,
,  , so (2.2) can be rewritten as
, so (2.2) can be rewritten as

thus one can get  or
or

and one notices that  ,
,  , then boundary entropy condition (2.2) is equivalent to
, then boundary entropy condition (2.2) is equivalent to

The proof for one-dimension case of Lemma 2.2 can be found in Pan and Lin's work [13], and the proof for  -dimension case is totally similar to one-dimension case; actually the idea of the proof first appears in Bardos et al.'s work [2], so the proof details for Lemma 2.2 are omitted here.
-dimension case is totally similar to one-dimension case; actually the idea of the proof first appears in Bardos et al.'s work [2], so the proof details for Lemma 2.2 are omitted here.
Lemma 2.3.
A piecewise smooth function  with smooth discontinuous surface is a weak entropy solution to the Riemann initial-boundary value problem (1.1) in the sense of (2.1) if and only if the following conditions are satisfied.
with smooth discontinuous surface is a weak entropy solution to the Riemann initial-boundary value problem (1.1) in the sense of (2.1) if and only if the following conditions are satisfied.
-
(i)
Rankine-Hugoniot condition: At any point
 on discontinuity surface
on discontinuity surface  of solution
of solution 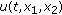 ,
, 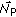 is a unit normal vector to
is a unit normal vector to 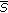 at
at  if
if  (2.6)
(2.6)
then

where  ,
,  .
.
For any constant  ,
,  ,
,

or equivalently

-
(ii)
Boundary entropy condition:
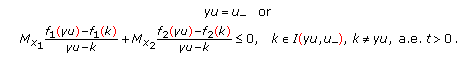 (2.10)
(2.10)
-
(iii)
Initial value condition:
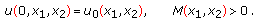 (2.11)
(2.11)
For piecewise smooth solution with smooth discontinuous surface, Rankine-Hugoniot condition (2.7), entropy conditions (2.8), (2.9) and initial value condition (2.11) are obviously satisfied, see also the previous famous works in [4, 7–9]. As in Lemma 2.2, boundary entropy condition (2.10) also holds. The proof of the converse in not difficult and is omitted here.
According to Bardos et al.'s work [2], we have the following Lemma.
Lemma 2.4.
If  is piecewise smooth weak entropy solution of (1.1) which satisfies the conditions of Lemma 2.3, then
is piecewise smooth weak entropy solution of (1.1) which satisfies the conditions of Lemma 2.3, then  is unique.
is unique.
According to the uniqueness of weak entropy solution, as long as the piecewise smooth function satisfying Lemma 2.3 is constructed, the weak entropy solution of Riemann initial-boundary value problem can be obtained.
3. Solution of Riemann Initial Value Problem
First, we study the Riemann initial value problem corresponding to the Riemann initial-boundary value problem (1.1) as follows:

Condition  For
For  ,
,

where  is a certain interval
is a certain interval  can be a finite number or
can be a finite number or  .
.
Condition  combines flux functions
combines flux functions  and curved boundary manifold
and curved boundary manifold  , providing necessary condition for the convex property of the new flux function which will be constructed in formula (4.5). The convex property clarifies whether the characteristics intersect or not, whether the weak solution satisfied internal entropy conditions (2.8) and (2.9) and boundary entropy condition (2.10), In addition, Condition
, providing necessary condition for the convex property of the new flux function which will be constructed in formula (4.5). The convex property clarifies whether the characteristics intersect or not, whether the weak solution satisfied internal entropy conditions (2.8) and (2.9) and boundary entropy condition (2.10), In addition, Condition  is easily satisfied, for example,
is easily satisfied, for example,  ,
,  , then
, then  , so Condition
, so Condition  holds. Here
holds. Here  is a cubic curve on the
is a cubic curve on the  plane, and it is strictly bending.
plane, and it is strictly bending.
Yang's work [10] showed that depending on whether the characteristics intersect or not, the weak entropy solution of (3.1) has two forms as follows.
Lemma 3.1 (see [10]).
Suppose ( ) holds. If
) holds. If  , then weak entropy solution of (3.1) is shock wave solution
, then weak entropy solution of (3.1) is shock wave solution  , and
, and

and discontinuity surface  is
is

where  ,
,  ,
,  .
.
Lemma 3.2 (see [10]).
Suppose that ( ) holds. If
) holds. If  , then weak entropy solution of (3.1) is rarefaction wave solution
, then weak entropy solution of (3.1) is rarefaction wave solution  , and
, and

where
 is the implicit function which satisfies
is the implicit function which satisfies

Theorem 3.3 (see [10]).
Suppose that ( ) holds. Given
) holds. Given  , then
, then
(i)if , weak entropy solution of(3.1)is and
, weak entropy solution of(3.1)is and  has a form as (3.3);
has a form as (3.3);
(ii)if  , weak entropy solution of (3.1) is
, weak entropy solution of (3.1) is  and
and  has a form as (3.5);
has a form as (3.5);
(iii) weak entropy solutions formed as (3.3) and (3.5) uniquely exist.
The weak entropy solutions constructed here are piecewise smooth and satisfy conditions (i) and (iii) of Lemma 2.3.
4. Solution of Riemann Initial-Boundary Value Problem
Now we restrict the weak entropy solutions of the Riemann initial value problem (3.1) constructed in Section 3 in region  , and they still satisfy conditions (i) and (iii) of Lemma 2.3. If they also satisfy the boundary entropy condition (ii) of Lemma 2.3, then they are the weak entropy solutions of Riemann initial-boundary value problem (1.1).
, and they still satisfy conditions (i) and (iii) of Lemma 2.3. If they also satisfy the boundary entropy condition (ii) of Lemma 2.3, then they are the weak entropy solutions of Riemann initial-boundary value problem (1.1).
Based on different Riemann data of  and
and  , the weak entropy solutions of the Riemann initial value problem (3.1) have the following five different behaviors when restricted in region
, the weak entropy solutions of the Riemann initial value problem (3.1) have the following five different behaviors when restricted in region  .
.
If  , the solution of (3.1) is shock wave and
, the solution of (3.1) is shock wave and

 is formed by moving
is formed by moving  along the direction of the vector
along the direction of the vector  , and the outward normal vector
, and the outward normal vector  of curve
of curve  is equal to
is equal to  . According to the angle between
. According to the angle between  and
and  , the solution restricted in
, the solution restricted in  has two behaviors as follows.
has two behaviors as follows.
Case 1.
If  and
and  .
.
See also Figure 1(a); it shows that the angle between  and
and  is an acute angle, the shock wave surface
is an acute angle, the shock wave surface  is outside region
is outside region  , and the solution is constant state formed as
, and the solution is constant state formed as

Case 2.
If  and
and  .
.
See also Figure 2; it shows that the angle between  and
and  is an obtuse angle, the shock wave surface
is an obtuse angle, the shock wave surface  is inside region
is inside region  , and the solution is shock wave formed as
, and the solution is shock wave formed as

If  , the solution of (3.1) is rarefaction wave
, the solution of (3.1) is rarefaction wave  and
and

 is formed by moving
is formed by moving  along the direction of the vector
along the direction of the vector  ,
,  is formed by moving
is formed by moving  along the direction of the vector
along the direction of the vector  , and the outward normal vector
, and the outward normal vector  of curve
of curve  is equal to
is equal to  .
.
We construct a new flux function

according to condition ( ),
),  ,
,  is convex, and
is convex, and  is monotonically increasing function, so
is monotonically increasing function, so  . And also
. And also

Thus,  . According to the angles between
. According to the angles between  ,
,  , and
, and  , the solution restricted in
, the solution restricted in  has three behaviors as follows.
has three behaviors as follows.
Case 3.
If  and
and  .
.
See also Figure 3; it shows that the angles between  ,
,  and
and  are obtuse angles, the rarefaction wave surfaces
are obtuse angles, the rarefaction wave surfaces  and
and  are both inside region
are both inside region  , and the solution is rarefaction wave formed as
, and the solution is rarefaction wave formed as

where  is the implicit function which satisfies (3.6).
is the implicit function which satisfies (3.6).
Case 4.
If  and
and  .
.
See also Figure 4(a); it shows that the angle between  and
and  is an obtuse angle, the angle between
is an obtuse angle, the angle between  and
and  is an acute angles, the rarefaction wave surface
is an acute angles, the rarefaction wave surface  is inside region
is inside region  , the rarefaction wave surface
, the rarefaction wave surface  is outside region
is outside region  , and the solution is rarefaction wave formed as
, and the solution is rarefaction wave formed as

where  is the implicit function which satisfies (3.6).
is the implicit function which satisfies (3.6).
Case 5.
If  and
and  .
.
See also Figure 5(a); it shows that the angles between  ,
,  , and
, and  are acute angles, the rarefaction wave surfaces
are acute angles, the rarefaction wave surfaces  and
and  are both outside region
are both outside region  , and the solution is constant state formed as
, and the solution is constant state formed as

Next, we verify the above five solutions all satisfying the boundary entropy condition (ii) of Lemma 2.3. By noticing the definition of  (4.5) and its convex property, the boundary entropy condition (ii) of Lemma 2.3 can be equivalent to the following formula
(4.5) and its convex property, the boundary entropy condition (ii) of Lemma 2.3 can be equivalent to the following formula

and thus we verify the above five solutions all satisfying the boundary entropy condition (4.10).
Case 1.
When  ,
,  , the shock wave solution is formed as (4.2). In this case,
, the shock wave solution is formed as (4.2). In this case,  since
since

and  , where
, where  is the extreme point of
is the extreme point of  . For
. For  , according to the convex property of
, according to the convex property of  , we have that
, we have that

and so the boundary entropy condition (4.10) is verified.
Case 2.
When  ,
,  , the shock wave solution is formed as (4.3). In this case,
, the shock wave solution is formed as (4.3). In this case,  , so the boundary entropy condition (4.10) is naturally verified.
, so the boundary entropy condition (4.10) is naturally verified.
Case 3.
When  ,
,  , the rarefaction wave solution is formed as (4.7). In this case,
, the rarefaction wave solution is formed as (4.7). In this case,  , and so the boundary entropy condition (4.10) is naturally verified.
, and so the boundary entropy condition (4.10) is naturally verified.
Case 4.
When  ,
,  , the rarefaction wave solution is formed as (4.8). In this case,
, the rarefaction wave solution is formed as (4.8). In this case,  ,
,  and
and  (see also Figure 4(b)), namely,
(see also Figure 4(b)), namely,  . For
. For  , according to the convex property of
, according to the convex property of  and Lagrange mean value theorem, there exists
and Lagrange mean value theorem, there exists  , satisfying
, satisfying

and so the boundary entropy condition (4.10) is verified.
Case 5.
When  ,
,  , the rarefaction wave solution is formed as (4.9). In this case,
, the rarefaction wave solution is formed as (4.9). In this case,  since
since  (see also Figure 5(b)) For
(see also Figure 5(b)) For  , according to the convex property of
, according to the convex property of  and Lagrange mean value theorem, there exists
and Lagrange mean value theorem, there exists  , satisfying
, satisfying

and so the boundary entropy condition (4.10) is verified.
In summary, we have the following theorem.
Theorem 4.1.
Suppose that ( ) holds. Given
) holds. Given  , then
, then
(i)if  and
and  , the solution of (1.1) is constant state and has form as (4.2),
, the solution of (1.1) is constant state and has form as (4.2),
(ii)if  and
and  , the solution of (1.1) is shock wave , and has form as (4.3),
, the solution of (1.1) is shock wave , and has form as (4.3),
(iii)if  and
and  , the solution of (1.1) is rarefaction wave
, the solution of (1.1) is rarefaction wave  and has a form as (4.7),
and has a form as (4.7),
(iv)if  and
and  , the solution of (1.1) is rarefaction wave
, the solution of (1.1) is rarefaction wave  and has a form as (4.8);
and has a form as (4.8);
(v)if  and
and  , the solution of (1.1) is constant state and has a form as (4.9).
, the solution of (1.1) is constant state and has a form as (4.9).
In addition the solutions formed as (4.2), (4.3), (4.7), (4.8), and (4.9) uniquely exist.
Corollary 4.2.
Suppose that  for
for  .
.  can be finite or
can be finite or  , and when
, and when  ,
,
(i)if  and
and  , the solution of (1.1) is rarefaction wave
, the solution of (1.1) is rarefaction wave  and has a form as (4.7),
and has a form as (4.7),
(ii)if  and
and  , the solution of (1.1) is rarefaction wave
, the solution of (1.1) is rarefaction wave  and has a form as (4.8),
and has a form as (4.8),
(iii)if  and
and  , the solution of (1.1) is constant state and has a form as (4.9),
, the solution of (1.1) is constant state and has a form as (4.9),
(iv)if  and
and  , the solution of (1.1) is constant state and has a form as (4.2),
, the solution of (1.1) is constant state and has a form as (4.2),
(v)if  and
and  , the solution of (1.1) is shock wave
, the solution of (1.1) is shock wave  and has a form as (4.3).
and has a form as (4.3).
Corollary 4.3.
The approach here for two-dimensional Riemann initial-boundary problem can be expanded to the case of general  -dimension.
-dimension.
5. An Example
Solve the following Riemann initial-boundary problem:

where  ,
,  ,
,  , and it denotes
, and it denotes  . Since
. Since  , we easily get
, we easily get  , and condition
, and condition  holds.
holds.
According to the different data of  and
and  , the behavior of the solution to Riemann initial-boundary problem (5.1) has a total of five situations; they can be described by the following five cases: (i)
, the behavior of the solution to Riemann initial-boundary problem (5.1) has a total of five situations; they can be described by the following five cases: (i)  ,
,  ; (ii)
; (ii)  ,
,  ; (iii)
; (iii)  ,
,  ; (iv)
; (iv)  ,
,  ; (v)
; (v)  ,
,  .
.
For case (i),  and
and

and thus the solution is constant state formed as

For case (ii),  and
and

and thus the solution is shock wave solution formed as

For case (iii),  and
and

namely,  , thus the solution is rarefaction wave formed as
, thus the solution is rarefaction wave formed as

Here, we only need to solve  , where
, where

To solve the following equation of  :
:

using Cardano formula, we can get the unique solution as

Since  is the solution of implicit function, we still need to verify
is the solution of implicit function, we still need to verify  satisfying the following three conditions: (a)
satisfying the following three conditions: (a)  ; (b)
; (b)  ; (c)
; (c)  . In fact, according to the next proposition, the above three conditions can be easily verified, and the detail the omitted here.
. In fact, according to the next proposition, the above three conditions can be easily verified, and the detail the omitted here.
Proposition 5.1.
For any real number  , the following formula holds:
, the following formula holds:

Proof.
Let

then  satisfies
satisfies

where  must be one root of (5.13). In fact,
must be one root of (5.13). In fact,  . Equation (5.13) at most has one real root; but
. Equation (5.13) at most has one real root; but  is its real root, thus
is its real root, thus  , and the proposition holds.
, and the proposition holds.
For case (iv),  and
and

namely,  , and thus the solution is rarefaction wave formed as
, and thus the solution is rarefaction wave formed as

where  has the same form as (5.10).
has the same form as (5.10).
For case (v),  and
and

namely,  , and thus the solution is constant state formed as
, and thus the solution is constant state formed as

References
Kruzkov SN: Generalized solutions of the Cauchy problem in the large for nonlinear equations of first order. Soviet Mathematics Doklady 1969, 10: 785-788.
Bardos C, le Roux AY, Nédélec J-C: First order quasilinear equations with boundary conditions. Communications in Partial Differential Equations 1979, 4(9):1017-1034. 10.1080/03605307908820117
Razafimandimby PA, Sango M: Weak solutions of a stochastic model for two-dimensional second grade fluids. Boundary Value Problems 2010, 2010:-47.
Conway E, Smoller J: Clobal solutions of the Cauchy problem for quasi-linear first-order equations in several space variables. Communications on Pure and Applied Mathematics 1966, 19: 95-105.
Lindquist WB: The scalar Riemann problem in two spatial dimensions: piecewise smoothness of solutions and its breakdown. SIAM Journal on Mathematical Analysis 1986, 17(5):1178-1197. 10.1137/0517082
Wagner DH: The Riemann problem in two space dimensions for a single conservation law. SIAM Journal on Mathematical Analysis 1983, 14(3):534-559. 10.1137/0514045
Zhang T, Zheng YX: Two-dimensional Riemann problem for a single conservation law. Transactions of the American Mathematical Society 1989, 312(2):589-619. 10.1090/S0002-9947-1989-0930070-3
Guckenheimer J: Shocks and rarefactions in two space dimensions. Archive for Rational Mechanics and Analysis 1975, 59(3):281-291.
Zheng Y: Systems of Conservation Laws: Two-Dimensional Riemann Problems, Progress in Nonlinear Differential Equations and Their Applications. Volume 38. Birkhäuser, Boston, Mass, USA; 2001:xvi+317.
Yang X: Multi-dimensional Riemann problem of scalar conservation law. Acta Mathematica Scientia 1999, 19(2):190-200.
Dubois F, LeFloch P: Boundary conditions for nonlinear hyperbolic systems of conservation laws. Journal of Differential Equations 1988, 71(1):93-122. 10.1016/0022-0396(88)90040-X
LeFloch P, Nédélec J-C: Explicit formula for weighted scalar nonlinear hyperbolic conservation laws. Transactions of the American Mathematical Society 1988, 308(2):667-683.
Pan T, Lin L: The global solution of the scalar nonconvex conservation law with boundary condition. Journal of Partial Differential Equations 1995, 8(4):371-383.
Pan T, Lin L: The global solution of the scalar nonconvex conservation law with boundary condition. (Continuation). Journal of Partial Differential Equations 1998, 11(1):1-8.
Pan T, Liu H, Nishihara K: Asymptotic stability of the rarefaction wave of a one-dimensional model system for compressible viscous gas with boundary. Japan Journal of Industrial and Applied Mathematics 1999, 16(3):431-441. 10.1007/BF03167367
Pan T, Jiu Q: Asymptotic behaviors of the solutions to scalar viscous conservation laws on bounded interval corresponding to rarefaction waves. Progress in Natural Science 1999, 9(12):948-952.
Pan T, Liu H: Asymptotic behaviors of the solution to an initial-boundary value problem for scalar viscous conservation laws. Applied Mathematics Letters 2002, 15(6):727-734. 10.1016/S0893-9659(02)00034-4
Pan T, Liu H, Nishihara K: Asymptotic behavior of a one-dimensional compressible viscous gas with free boundary. SIAM Journal on Mathematical Analysis 2002, 34(2):273-291. 10.1137/S0036141001385745
Acknowledgment
This work is supported by the National Natural Science Foundation of China (10771087, 61078040), the Natural Science Foundation of Guangdong Province (7005948).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, H., Pan, T. Two-Dimension Riemann Initial-Boundary Value Problem of Scalar Conservation Laws with Curved Boundary. Bound Value Probl 2011, 138396 (2011). https://doi.org/10.1155/2011/138396
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/138396
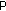 on discontinuity surface
on discontinuity surface 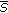 of solution
of solution 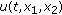 ,
, 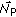 is a unit normal vector to
is a unit normal vector to 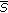 at
at  if
if