- Research Article
- Open access
- Published:
Existence of Positive, Negative, and Sign-Changing Solutions to Discrete Boundary Value Problems
Boundary Value Problems volume 2011, Article number: 172818 (2011)
Abstract
By using critical point theory, Lyapunov-Schmidt reduction method, and characterization of the Brouwer degree of critical points, sufficient conditions to guarantee the existence of five or six solutions together with their sign properties to discrete second-order two-point boundary value problem are obtained. An example is also given to demonstrate our main result.
1. Introduction
Let  ,
,  , and
, and  denote the sets of all natural numbers, integers, and real numbers, respectively. For
denote the sets of all natural numbers, integers, and real numbers, respectively. For  , define
, define  , when
, when  .
.  is the forward difference operator defined by
is the forward difference operator defined by  .
.
Consider the following discrete second-order two-point boundary value problem (BVP for short):

where  is a given integer.
is a given integer.
By a solution  to the BVP (1.1), we mean a real sequence
to the BVP (1.1), we mean a real sequence  satisfying (1.1). For
satisfying (1.1). For  with
with  , we say that
, we say that  if there exists at least one
if there exists at least one  such that
such that  . We say that
. We say that  is positive (and write
is positive (and write  ) if for all
) if for all  , and
, and  :
:  , and similarly,
, and similarly,  is negative (
is negative ( ) if for all
) if for all  , and
, and  . We say that
. We say that  is sign-changing if
is sign-changing if  is neither positive nor negative. Under convenient assumptions, we will prove the existence of five or six solutions to (1.1), which include positive, negative, and sign-changing solutions.
is neither positive nor negative. Under convenient assumptions, we will prove the existence of five or six solutions to (1.1), which include positive, negative, and sign-changing solutions.
Difference BVP has widely occurred as the mathematical models describing real-life situations in mathematical physics, finite elasticity, combinatorial analysis, and so forth; for example, see [1, 2]. And many scholars have investigated difference BVP independently mainly for two reasons. The first one is that the behavior of discrete systems is sometimes sharply different from the behavior of the corresponding continuous systems. For example, every solution of logistic equation  is monotone, but its discrete analogue
is monotone, but its discrete analogue  has chaotic solutions; see [3] for details. The second one is that there is a fundamental relationship between solutions to continuous systems and the corresponding discrete systems by employing discrete variable methods [1]. The classical results on difference BVP employs numerical analysis and features from the linear and nonlinear operator theory, such as fixed point theorems. We remark that, usually, the application of the fixed point theorems yields existence results only.
has chaotic solutions; see [3] for details. The second one is that there is a fundamental relationship between solutions to continuous systems and the corresponding discrete systems by employing discrete variable methods [1]. The classical results on difference BVP employs numerical analysis and features from the linear and nonlinear operator theory, such as fixed point theorems. We remark that, usually, the application of the fixed point theorems yields existence results only.
Recently, however, a few scholars have used critical point theory to deal with the existence of multiple solutions to difference BVP. For example, in 2004, Agarwal et al. [4] employed the mountain pass lemma to study (1.1) with  and obtained the existence of multiple solutions. Very recently, Zheng and Zhang [5] obtained the existence of exactly three solutions to (1.1) by making use of three-critical-point theorem and analytic techniques. We also refer to [6–9] for more results on the difference BVP by using critical point theory. The application of critical point theory to difference BVP represents an important advance as it allows to prove multiplicity results as well.
and obtained the existence of multiple solutions. Very recently, Zheng and Zhang [5] obtained the existence of exactly three solutions to (1.1) by making use of three-critical-point theorem and analytic techniques. We also refer to [6–9] for more results on the difference BVP by using critical point theory. The application of critical point theory to difference BVP represents an important advance as it allows to prove multiplicity results as well.
Here, by using critical point theory again, as well as Lyapunov-Schmidt reduction method and degree theory, a sharp condition to guarantee the existence of five or six solutions together with their sign properties to (1.1) is obtained. And this paper offers, to the best of our knowledge, a new method to deal with the sign of solutions in the discrete case.
Here, we assume that  and
and

Hence,  grows asymptotically linear at infinity.
grows asymptotically linear at infinity.
The solvability of (1.1) depends on the properties of  both at zero and at infinity. If
both at zero and at infinity. If

where  is one of the eigenvalues of the eigenvalue problem
is one of the eigenvalues of the eigenvalue problem

then we say that (1.1) is resonant at infinity (or at zero); otherwise, we say that (1.1) is nonresonant at infinity (or at zero). On the eigenvalue problem (1.4), the following results hold (see [1] for details).
Proposition 1.1.
For the eigenvalue problem (1.4), the eigenvalues are

and the corresponding eigenfunctions with  are
are  .
.
Remark 1.2.
-
(i)
The set of functions
 is orthogonal on
is orthogonal on 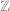 with respect to the weight function
with respect to the weight function  ; that is,
; that is,  (1.6)
(1.6)
Moreover, for each  .
.
-
(ii)
It is easy to see that
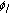 is positive and
is positive and 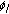 changes sign for each
changes sign for each 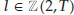 ; that is,
; that is,  :
: 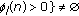 and
and 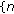 :
: 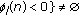 for
for 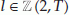 .
.
The main result of this paper is as follows.
Theorem 1.3.
If  with
with  , and
, and  , then (1.1) has at least five solutions. Moreover, one of the following cases occurs:
, then (1.1) has at least five solutions. Moreover, one of the following cases occurs:
-
(i)
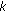 is even and (1.1) has two sign-changing solutions,
is even and (1.1) has two sign-changing solutions, -
(ii)
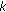 is even and (1.1) has six solutions, three of which are of the same sign,
is even and (1.1) has six solutions, three of which are of the same sign, -
(iii)
 is odd and (1.1) has two sigh-changing solutions,
is odd and (1.1) has two sigh-changing solutions, -
(iv)
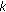 is odd and (1.1) has three solutions of the same sign.
is odd and (1.1) has three solutions of the same sign.
Remark 1.4.
The assumption  in Theorem 1.3 is sharp in the sense that when
in Theorem 1.3 is sharp in the sense that when  for
for  , Theorem 1.4 of [5] gives sufficient conditions for (1.1) to have exactly three solutions with some restrictive conditions.
, Theorem 1.4 of [5] gives sufficient conditions for (1.1) to have exactly three solutions with some restrictive conditions.
Example 1.5.
Consider the BVP

where  is defined as follows:
is defined as follows:

It is easy to verify that  ,
,  , and
, and  . So, all the conditions in Theorem 1.3 are satisfied with
. So, all the conditions in Theorem 1.3 are satisfied with  . And hence (1.7) has at least five solutions, among which two sign-changing solutions or three solutions of the same sign.
. And hence (1.7) has at least five solutions, among which two sign-changing solutions or three solutions of the same sign.
By the computation of critical groups, for  , we have the following.
, we have the following.
Corollary 1.6 (see Remark 3.7 below).
If  , and
, and  , then (1.1) has at least one positive solution and one negative solution.
, then (1.1) has at least one positive solution and one negative solution.
2. Preliminaries
Let

Then,  is a
is a  -dimensional Hilbert space with inner product
-dimensional Hilbert space with inner product

by which the norm  can be induced by
can be induced by

Here,  denotes the Euclidean norm in
denotes the Euclidean norm in  , and
, and  denotes the usual inner product in
denotes the usual inner product in  .
.
Define

Then, the functional  is of class
is of class  with
with

So, solutions to (1.1) are precisely the critical points of  in
in  .
.
As we have mentioned, we will use critical point theory, Lyapunov-Schmidt reduction method, and degree theory to prove our result. Let us collect some results that will be used below. One can refer to [10–12] for more details.
Let  be a Hilbert space and
be a Hilbert space and  . Denote
. Denote

for  . The following is the definition of the Palais-Smale (PS) compactness condition.
. The following is the definition of the Palais-Smale (PS) compactness condition.
Definition 2.1.
The functional  satisfies the (PS) condition if any sequence
satisfies the (PS) condition if any sequence  such that
such that  is bounded and
is bounded and  as
as  has a convergent subsequence.
has a convergent subsequence.
In [13], Cerami introduced a weak version of the (PS) condition as follows.
Definition 2.2.
The functional  satisfies the Cerami (C) condition if any sequence
satisfies the Cerami (C) condition if any sequence  such that
such that  is bounded and
is bounded and  , as
, as  has a convergent subsequence.
has a convergent subsequence.
If  satisfies the (PS) condition or the (C) condition, then
satisfies the (PS) condition or the (C) condition, then  satisfies the following deformation condition which is essential in critical point theory (cf. [14, 15]).
satisfies the following deformation condition which is essential in critical point theory (cf. [14, 15]).
Definition 2.3.
The functional  satisfies the (
satisfies the ( ) condition at the level
) condition at the level  if for any
if for any  and any neighborhood of
and any neighborhood of  , there are
, there are  and a continuous deformation
and a continuous deformation  such that
such that
-
(i)
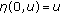 for all
for all 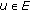 ,
, -
(ii)
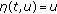 for all
for all  ,
, -
(iii)
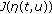 is non-increasing in
is non-increasing in 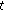 for any
for any 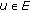 ,
, -
(iv)
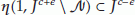 .
.
 satisfies the (D) condition if
satisfies the (D) condition if  satisfies the (
satisfies the ( ) condition for all
) condition for all  .
.
Let  denote singular homology with coefficients in a field
denote singular homology with coefficients in a field  . If
. If  is a critical point of
is a critical point of  with critical level
with critical level  , then the critical groups of
, then the critical groups of  are defined by
are defined by

Suppose that  is strictly bounded from below by
is strictly bounded from below by  and that
and that  satisfies (
satisfies ( ) for all
) for all  . Then, the
. Then, the  th critical group at infinity of
th critical group at infinity of  is defined in [16] as
is defined in [16] as

Due to the condition  , these groups are not dependent on the choice of
, these groups are not dependent on the choice of  .
.
Assume that  and
and  satisfies the (D) condition. The Morse-type numbers of the pair
satisfies the (D) condition. The Morse-type numbers of the pair  are defined by
are defined by  , and the Betti numbers of the pair
, and the Betti numbers of the pair  are defined by
are defined by  . By Morse theory [10, 11], the following relations hold:
. By Morse theory [10, 11], the following relations hold:


It follows that  for all
for all  . If
. If  , then
, then  for all
for all  . Thus, when
. Thus, when  for some
for some  must have a critical point
must have a critical point  with
with  .
.
The critical groups of  at an isolated critical point
at an isolated critical point  describe the local behavior of
describe the local behavior of  near
near  , while the critical groups of
, while the critical groups of  at infinity describe the global property of
at infinity describe the global property of  . In most applications, unknown critical points will be found from (2.9) or (2.10) if we can compute both the critical groups at known critical points and the critical groups at infinity. Thus, the computation of the critical groups is very important. Now, we collect some useful results on computation of critical groups which will be employed in our discussion.
. In most applications, unknown critical points will be found from (2.9) or (2.10) if we can compute both the critical groups at known critical points and the critical groups at infinity. Thus, the computation of the critical groups is very important. Now, we collect some useful results on computation of critical groups which will be employed in our discussion.
Proposition 2.4 (see [16]).
Let  be a real Hilbert space and
be a real Hilbert space and  . Suppose that
. Suppose that  splits as
splits as  such that
such that  is bounded from below on
is bounded from below on  and
and  for
for  as
as  . Then
. Then  for
for  .
.
Proposition 2.5 (see [17]).
Let  be a separable Hilbert space with inner product
be a separable Hilbert space with inner product  and corresponding norm
and corresponding norm  ,
,  ,
,  closed subspaces of
closed subspaces of  such that
such that  . Assume that
. Assume that  satisfies the (PS) condition and the critical values of
satisfies the (PS) condition and the critical values of  are bounded from below. If there is a real number
are bounded from below. If there is a real number  such that for all
such that for all  and
and  , there holds
, there holds

then there exists a  -functional
-functional  :
:  such that
such that

Moreover, if  and
and  , then
, then  .
.
Let  denote the open ball in
denote the open ball in  about 0 of the radius
about 0 of the radius  , and let
, and let  denote its boundary.
denote its boundary.
Lemma 2.6 (Mountain Pass Lemma [10, 11]).
Let  be a real Banach space and
be a real Banach space and  satisfying the (PS) condition. Suppose that
satisfying the (PS) condition. Suppose that  and
and
(J1) there are constants  such that
such that  , and
, and
(J2) there is a  such that
such that  .
.
Then,  possesses a critical value
possesses a critical value  . Moreover,
. Moreover,  can be characterized as
can be characterized as

where

Definition 2.7 (Mountain pass point).
An isolated critical point  of
of  is called a mountain pass point if
is called a mountain pass point if  .
.
To compute the critical groups of a mountain pass point, we have the following result.
Proposition 2.8 (see [11]).
Let  be a real Hilbert space. Suppose that
be a real Hilbert space. Suppose that  has a mountain pass point
has a mountain pass point  and that
and that  is a Fredholm operator with finite Morse index satisfying
is a Fredholm operator with finite Morse index satisfying

Then,

The following theorem gives a relation between the Leray-Schauder degree and the critical groups.
Let  be a real Hilbert space, and let
be a real Hilbert space, and let  be a function satisfying the (PS) condition. Assume that
be a function satisfying the (PS) condition. Assume that  , where
, where  :
:  is a completely continuous operator. If
is a completely continuous operator. If  is an isolated critical point of
is an isolated critical point of  , that is, there exists a neighborhood
, that is, there exists a neighborhood  of
of  , such that
, such that  is the only critical point of
is the only critical point of  in
in  , then
, then

where  denotes the Leray-Schauder degree.
denotes the Leray-Schauder degree.
Finally, we state a global version of the Lyapunov-Schmidt reduction method.
Lemma 2.10 (see [18]).
Let  be a real separable Hilbert space. Let
be a real separable Hilbert space. Let  and
and  be closed subspaces of
be closed subspaces of  such that
such that  and
and  . If there are
. If there are  such that for all
such that for all  ,
,

then the following results hold.
(i) There exists a continuous function  :
:  such that
such that

Moreover,  is the unique member of
is the unique member of  such that
such that

(ii) The function  :
:  defined by
defined by  is of class
is of class  , and
, and

(iii) An element  is a critical point of
is a critical point of  if and only if
if and only if  is a critical point of
is a critical point of  .
.
(iv) Let  and
and  be the projection onto
be the projection onto  across
across  . Let
. Let  and
and  be open bounded regions such that
be open bounded regions such that

If  for
for  , then
, then

where  denotes the Leray-Schauder degree.
denotes the Leray-Schauder degree.
(v) If  is a critical point of mountain pass type of
is a critical point of mountain pass type of  , then
, then  is a critical point of mountain pass type of
is a critical point of mountain pass type of  .
.
3. Proof of Theorem 1.3
In this section, firstly, we obtain a positive solution  and a negative solution
and a negative solution  with
with  to (1.1) by using cutoff technique and the mountain pass lemma. Then, we give a precise computation of
to (1.1) by using cutoff technique and the mountain pass lemma. Then, we give a precise computation of  . And we remark that under the assumptions of Theorem 1.3,
. And we remark that under the assumptions of Theorem 1.3,  can be completely computed by using Propositions 2.4 and 2.5. Based on these results, four nontrivial solutions
can be completely computed by using Propositions 2.4 and 2.5. Based on these results, four nontrivial solutions  to (1.1) can be obtained by (2.9) or (2.10). However, it seems difficult to obtain the sign property of
to (1.1) can be obtained by (2.9) or (2.10). However, it seems difficult to obtain the sign property of  and
and  through their depiction of critical groups. To conquer this difficulty, we compute the Brouwer degree of the sets of positive solutions and negative solutions to (1.1). Finally, the third nontrivial solution to (1.1) is obtained by Lyapunov-Schmidt reduction method, and its characterization of the local degree results in one or two more nontrivial solutions to (1.1) together with their sign property.
through their depiction of critical groups. To conquer this difficulty, we compute the Brouwer degree of the sets of positive solutions and negative solutions to (1.1). Finally, the third nontrivial solution to (1.1) is obtained by Lyapunov-Schmidt reduction method, and its characterization of the local degree results in one or two more nontrivial solutions to (1.1) together with their sign property.
Let

and  . The functionals
. The functionals  are defined as
are defined as

Remark 3.1.
From the definitions of  and
and  , it is easy to see that if
, it is easy to see that if  is a critical point of
is a critical point of  (or
(or  ), then
), then  (or
(or  ).
).
Lemma 3.2.
The functionals  satisfy the (PS) condition; that is, every sequence
satisfy the (PS) condition; that is, every sequence  in
in  such that
such that  is bounded, and
is bounded, and  as
as  has a convergent subsequence.
has a convergent subsequence.
Proof.
We only prove the case of  . The case of
. The case of  is completely similar. Since
is completely similar. Since  is finite dimensional, it suffices to show that
is finite dimensional, it suffices to show that  is bounded. Suppose that
is bounded. Suppose that  is unbounded. Passing to a subsequence, we may assume that
is unbounded. Passing to a subsequence, we may assume that  and for each
and for each  , either
, either  or
or  is bounded.
is bounded.
Set  . For a subsequence,
. For a subsequence,  converges to some
converges to some  with
with  . Since for all
. Since for all  , we have
, we have

Hence,

If  , then
, then

where  ,
,  . If
. If  is bounded, then
is bounded, then

Letting  in (3.4), we have
in (3.4), we have

which implies that  satisfies
satisfies

Because  , we see that if
, we see that if  is a solution to (3.8), then
is a solution to (3.8), then  is positive. Since this contradicts
is positive. Since this contradicts  , we conclude that
, we conclude that  is the only solution to (3.8). A contradiction to
is the only solution to (3.8). A contradiction to  .
.
Lemma 3.3.
Under the conditions of Theorem 1.3,  has a positive mountain pass-type critical point
has a positive mountain pass-type critical point  with
with  has a negative mountain pass-type critical point
has a negative mountain pass-type critical point  with
with  .
.
Proof.
We only prove the case of  . Firstly, we will prove that
. Firstly, we will prove that  satisfies all the conditions in Lemma 2.6. And hence,
satisfies all the conditions in Lemma 2.6. And hence,  has at least one nonzero critical point
has at least one nonzero critical point  . In fact,
. In fact,  , and
, and  satisfies the (PS) condition by Lemma 3.2. Clearly,
satisfies the (PS) condition by Lemma 3.2. Clearly,  . Thus, we still have to show that
. Thus, we still have to show that  satisfies (J1), (J2). To verify (J1), set
satisfies (J1), (J2). To verify (J1), set  , then for any
, then for any  , there exists
, there exists  , such that
, such that

So, by Taylor series expansion,

Take  , then
, then  . If we set
. If we set  , then
, then

Since for all  , if
, if  , then
, then  for every
for every  and hence
and hence

where  ,
,  . If we take
. If we take

then  . And hence, (J1) holds.
. And hence, (J1) holds.
To verify (J2), note that  implies that there exist
implies that there exist  and
and  , such that
, such that

So, if we take  with
with  , then
, then

So, if we take  sufficiently large such that
sufficiently large such that  and for
and for  , then (J2) holds.
, then (J2) holds.
Now, by Lemma 2.6,  has at least a nonzero critical point
has at least a nonzero critical point  . And for all
. And for all  , we claim that
, we claim that  . If not, set
. If not, set  , then for all
, then for all  . By
. By  for all
for all  . Hence,
. Hence,  .
.
In the following, we will compute the critical groups  by using Proposition 2.8.
by using Proposition 2.8.
Assume that

and that there exists  such that
such that

This implies that  satisfies
satisfies

Hence, the eigenvalue problem

has an eigenvalue  . Condition
. Condition  implies that 1 must be a simple eigenvalue; see [1]. So,
implies that 1 must be a simple eigenvalue; see [1]. So,  . Since
. Since  is finite dimensional, the Morse index of
is finite dimensional, the Morse index of  must be finite and
must be finite and  must be a Fredholm operator. By Proposition 2.8,
must be a Fredholm operator. By Proposition 2.8,  . Finally, choose the neighborhood
. Finally, choose the neighborhood  of
of  such that
such that  for all
for all  , then
, then

The proof is complete.
Lemma 3.4.
By  , one has
, one has

Proof.
By assumption, we have  and for all
and for all  ,
,

which implies that 0 is a local minimizer of both  and
and  . Hence, (3.21) holds.
. Hence, (3.21) holds.
Remark 3.5.
Under the conditions of Theorem 1.3, we have

We will use Propositions 2.4 and 2.5 to prove (3.23). Very similar to the proof of Lemma 3.2, we can prove that  satisfies the (PS) condition. And it is easy to prove that
satisfies the (PS) condition. And it is easy to prove that  satisfies (2.11). In fact, let
satisfies (2.11). In fact, let

By  , for all
, for all  and
and  , we have
, we have

Hence, if we set  , then (2.11) holds.
, then (2.11) holds.
Now, noticing that  implies that there exist
implies that there exist  ,
,  and
and  such that
such that

Hence, we have


Then, (3.23) is proved by Propositions 2.4 and 2.5.
Remark 3.6.
Following the proof of Theorem 3.1 in [17], (3.23) implies that there must exist a critical point  of
of  satisfying
satisfying

It is known that the critical groups are useful in distinguishing critical points. So far, we have obtained four critical points 0,  ,
,  , and
, and  together with their characterization of critical groups. Assume that 0,
together with their characterization of critical groups. Assume that 0,  ,
,  , and
, and  are the only critical points of
are the only critical points of  . Then, the Morse inequality (2.10) becomes
. Then, the Morse inequality (2.10) becomes

This is impossible. Thus,  must have at least one more critical point
must have at least one more critical point  . Hence, (1.1) has at least five solutions. However, it seems difficult to obtain the sign property of
. Hence, (1.1) has at least five solutions. However, it seems difficult to obtain the sign property of  and
and  . To obtain more refined results, we seek the third nontrivial solution
. To obtain more refined results, we seek the third nontrivial solution  to (1.1) by Lyapunov-Schmidt reduction method and then its characterization of the local degree results in one or two more nontrivial solutions to (1.1) together with their sign property.
to (1.1) by Lyapunov-Schmidt reduction method and then its characterization of the local degree results in one or two more nontrivial solutions to (1.1) together with their sign property.
Remark 3.7.
The condition  in Theorem 1.3 is necessary to obtain three or more nontrivial solutions to (1.1). In fact, if
in Theorem 1.3 is necessary to obtain three or more nontrivial solutions to (1.1). In fact, if  , then we have
, then we have

Hence,  may coincide with
may coincide with  or
or  which becomes an obstacle to seek other critical points by using Morse inequality. If
which becomes an obstacle to seek other critical points by using Morse inequality. If  , then
, then

Hence, one cannot exclude the possibility of  .
.
To compute the degree of the set of positive (or negative) solutions to (1.1), we need the following lemma.
Lemma 3.8.
There exists  large enough, such that
large enough, such that

Proof.
We only prove the case of  . For any
. For any  , define
, define  as
as

Let  . The functional
. The functional  :
:  is defined as
is defined as

It is obvious that  is of class
is of class  and its critical points are precisely solutions to
and its critical points are precisely solutions to

Since  , we see that if
, we see that if  is a solution to (3.36), then
is a solution to (3.36), then  is positive. Because this contradicts
is positive. Because this contradicts  , we conclude that
, we conclude that  is the only critical point of
is the only critical point of  .
.
We claim that if  is a ball in
is a ball in  containing zero, then
containing zero, then  . In fact, since
. In fact, since  and
and  for
for  . Hence, for
. Hence, for  , we have
, we have

where we have used the fact that  is positive on
is positive on  . Then, for each
. Then, for each  and
and  , we have
, we have

Hence, by invariance under homotopy of Brouwer degree, we have

where  .
.
Now, let  . We claim that for
. We claim that for  large enough and for all
large enough and for all  , the function
, the function  has no zero on
has no zero on  .
.
In fact, we have proved that for all  and for all
and for all  , we have
, we have

On the other hand, by the definition of  , for all
, for all  , there exists
, there exists  large enough such that
large enough such that  for
for  . Since
. Since  , for
, for  , take
, take  , then
, then

For  , take
, take  , then
, then

Hence, if we take  , then for
, then for  , we have
, we have  , and for
, and for  , we have
, we have  . So, if we let
. So, if we let

then  for all
for all  . And for all
. And for all  , we have
, we have

So far, we have proved that for  large enough,
large enough,  has no zero point on
has no zero point on  for each
for each  . Hence, by invariance under homotopy of Brouwer degree, we obtain
. Hence, by invariance under homotopy of Brouwer degree, we obtain

This completes the proof.
Remark 3.9.
By Theorem 2.9 and the above results, we have the following characterization of degree of critical points.
If  (
( ) is a neighborhood of
) is a neighborhood of  (
( ) containing no other critical points, then
) containing no other critical points, then

Assume that  is a ball centered at zero containing on other critical points, then
is a ball centered at zero containing on other critical points, then

Hence, if  is a bounded region containing the positive critical points and no other critical points, then by (3.33) we have
is a bounded region containing the positive critical points and no other critical points, then by (3.33) we have

Similarly, we see that if  is a bounded region containing the negative critical points and no other critical points, then
is a bounded region containing the negative critical points and no other critical points, then

Now, we can give the proof of Theorem 1.3.
Proof of Theorem 1.3.
The functional  satisfies (2.18) in Lemma 2.10 due to the fact that
satisfies (2.18) in Lemma 2.10 due to the fact that  satisfies (2.11). Hence, by Lemma 2.10, there exists
satisfies (2.11). Hence, by Lemma 2.10, there exists  such that
such that

Moreover,  is the unique member of
is the unique member of  such that
such that

The function  defined by
defined by  is of class
is of class  . Because
. Because  , (3.27) implies that
, (3.27) implies that  as
as  . Since
. Since  , there must exist
, there must exist  such that
such that  . Take
. Take  , then
, then  by (iii) of Lemma 2.10. If
by (iii) of Lemma 2.10. If  is a neighborhood of
is a neighborhood of  containing no other critical points of
containing no other critical points of  , taking
, taking  , then
, then  . Then, by part (iv) of Lemma 2.10, we have
. Then, by part (iv) of Lemma 2.10, we have

Suppose that  Is Even
Is Even
Let  be large enough so that if
be large enough so that if  , then
, then  . Because
. Because  and
and  is of class
is of class  , there exists
, there exists  such that
such that  for
for  . Because
. Because  is coercive,
is coercive,  . Hence, if we set
. Hence, if we set  :
:  , then by (iv) of Lemma 2.10, we have
, then by (iv) of Lemma 2.10, we have

Suppose that  is finite. Let
is finite. Let  ,
,  , and
, and  be disjoint open bounded regions in
be disjoint open bounded regions in  such that
such that  is the set of positive critical points of
is the set of positive critical points of  , and
, and  is the set of negative critical points of
is the set of negative critical points of  . So far, we have proved that
. So far, we have proved that

(i) If  , then
, then  is sign changing. Let
is sign changing. Let  denote an open bounded region disjoint from
denote an open bounded region disjoint from  such that
such that  . By the excision property of Brouwer degree, we have
. By the excision property of Brouwer degree, we have

Thus, by Kronecker existence property of Brouwer degree, we see that there must exist  such that
such that  , which proves that (1.1) has at least five solutions. In this case, both
, which proves that (1.1) has at least five solutions. In this case, both  and
and  change sign.
change sign.
-
(ii)
Suppose now that
 . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  . Let
. Let  be a neighborhood of
be a neighborhood of 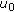 such that
such that 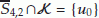 . By Lemma 3.3, there exists a critical point of mountain pass type
. By Lemma 3.3, there exists a critical point of mountain pass type 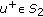 such that if
such that if  is a neighborhood of
is a neighborhood of 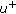 such that
such that  , then
, then 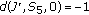 . Thus,
. Thus, 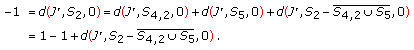 (3.56)
(3.56)
Thus, by Kronecker existence property of Brouwer degree, there exists  such that
such that  . Finally,
. Finally,

Thus, there must exist  such that
such that  . Thus, the set
. Thus, the set  together with a critical point
together with a critical point  of
of  in
in  shows that (1.1) has five nontrivial solutions. Since
shows that (1.1) has five nontrivial solutions. Since  and
and  ,
,  is a sign-changing solution, and
is a sign-changing solution, and  ,
,  , and
, and  have the same sign. This completes the proof of Theorem 1.3, when
have the same sign. This completes the proof of Theorem 1.3, when  is even.
is even.
Suppose that  Is Odd
Is Odd
-
(iii)
Let
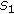 ,
, 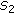 , and
, and 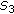 be as above. If
be as above. If 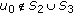 , the proof follows very closely that of the case (i).
, the proof follows very closely that of the case (i). -
(iv)
Suppose that
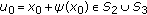 , hence
, hence  . Because
. Because 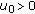 , there exists
, there exists  such that
such that 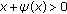 if
if  . So, if
. So, if 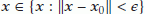 , then
, then  and
and 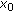 is a local maximum of
is a local maximum of 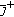 . Since we are assuming (1.1) to have only finitely many solutions,
. Since we are assuming (1.1) to have only finitely many solutions, 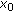 is a strictly local maximum of
is a strictly local maximum of 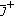 . Let
. Let 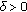 be such that
be such that 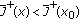 if
if  . Since
. Since 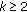 ,
, 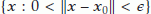 is path connected. Thus,
is path connected. Thus,  is not a critical point of mountain pass type. By Lemma 3.3,
is not a critical point of mountain pass type. By Lemma 3.3, 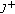 has a critical point of mountain pass type
has a critical point of mountain pass type  . By (v) of Lemma 2.10,
. By (v) of Lemma 2.10, 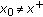 , and hence
, and hence  . Let
. Let  be neighborhoods of
be neighborhoods of 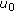 and
and  , respectively, such that
, respectively, such that 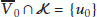 and
and 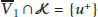 . Thus,
. Thus,  (3.58)
(3.58)
Thus, by Kronecker existence property of Brouwer degree, there exists a third positive solution  . So far, we have proved that (1.1) has at least four nontrivial solutions
. So far, we have proved that (1.1) has at least four nontrivial solutions  and that
and that  have the same sign. This proves Theorem 1.3.
have the same sign. This proves Theorem 1.3.
References
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Sharkovsky AN, Maĭstrenko YL, Romanenko EY: Difference Equations and Their Applications, Mathematics and Its Applications. Volume 250. Kluwer Academic, Dordrecht, The Netherlands; 1993:xii+358.
May RM: Simple mathematical models with very complicated dynamics. Nature 1976, 261: 459-466. 10.1038/261459a0
Agarwal RP, Perera K, O'Regan D: Multiple positive solutions of singular and nonsingular discrete problems via variational methods. Nonlinear Analysis. Theory, Methods & Applications 2004, 58(1-2):69-73. 10.1016/j.na.2003.11.012
Zheng B, Zhang Q: Existence and multiplicity of solutions of second-order difference boundary value problems. Acta Applicandae Mathematicae 2010, 110(1):131-152. 10.1007/s10440-008-9389-x
Cai X, Yu J: Existence theorems for second-order discrete boundary value problems. Journal of Mathematical Analysis and Applications 2006, 320(2):649-661. 10.1016/j.jmaa.2005.07.029
Jiang L, Zhou Z: Existence of nontrivial solutions for discrete nonlinear two point boundary value problems. Applied Mathematics and Computation 2006, 180(1):318-329. 10.1016/j.amc.2005.12.018
Liang H, Weng P: Existence and multiple solutions for a second-order difference boundary value problem via critical point theory. Journal of Mathematical Analysis and Applications 2007, 326(1):511-520. 10.1016/j.jmaa.2006.03.017
Aprahamian M, Souroujon D, Tersian S: Decreasing and fast solutions for a second-order difference equation related to Fisher-Kolmogorov's equation. Journal of Mathematical Analysis and Applications 2010, 363(1):97-110. 10.1016/j.jmaa.2009.08.009
Mawhin J, Willem M: Critical Point Theory and Hamiltonian Systems, Applied Mathematical Sciences. Volume 74. Springer, New York, NY, USA; 1989:xiv+277.
Chang K-C: Infinite-Dimensional Morse Theory and Multiple Solution Problems. Birkhäuser, Boston, Mass, USA; 1993:x+312.
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Cerami G: An existence criterion for the critical points on unbounded manifolds. Istituto Lombardo. Accademia di Scienze e Lettere. Rendiconti A 1978, 112(2):332-336.
Bartolo P, Benci V, Fortunato D: Abstract critical point theorems and applications to some nonlinear problems with "strong" resonance at infinity. Nonlinear Analysis. Theory, Methods & Applications 1983, 7(9):981-1012. 10.1016/0362-546X(83)90115-3
Chang KC: Solutions of asymptotically linear operator equations via Morse theory. Communications on Pure and Applied Mathematics 1981, 34(5):693-712. 10.1002/cpa.3160340503
Bartsch T, Li SJ: Critical point theory for asymptotically quadratic functionals and applications to problems with resonance. Nonlinear Analysis. Theory, Methods & Applications 1997, 28(3):419-441. 10.1016/0362-546X(95)00167-T
Liu S, Li S: Critical groups at infinity, saddle point reduction and elliptic resonant problems. Communications in Contemporary Mathematics 2003, 5(5):761-773. 10.1142/S0219199703001129
Castro A, Cossio J: Multiple solutions for a nonlinear Dirichlet problem. SIAM Journal on Mathematical Analysis 1994, 25(6):1554-1561. 10.1137/S0036141092230106
Acknowledgments
Project supported by National Natural Science Foundation of China (no. 11026059) and Foundation for Distinguished Young Talents in Higher Education of Guangdong, China (no. LYM09105).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zheng, B., Xiao, H. & Shi, H. Existence of Positive, Negative, and Sign-Changing Solutions to Discrete Boundary Value Problems. Bound Value Probl 2011, 172818 (2011). https://doi.org/10.1155/2011/172818
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/172818
 is orthogonal on
is orthogonal on 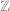 with respect to the weight function
with respect to the weight function  ; that is,
; that is, 
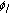 is positive and
is positive and 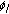 changes sign for each
changes sign for each 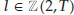 ; that is,
; that is,  :
: 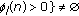 and
and 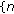 :
: 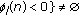 for
for 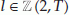 .
.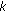 is even and (1.1) has two sign-changing solutions,
is even and (1.1) has two sign-changing solutions,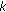 is even and (1.1) has six solutions, three of which are of the same sign,
is even and (1.1) has six solutions, three of which are of the same sign, is odd and (1.1) has two sigh-changing solutions,
is odd and (1.1) has two sigh-changing solutions,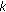 is odd and (1.1) has three solutions of the same sign.
is odd and (1.1) has three solutions of the same sign.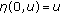 for all
for all 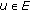 ,
,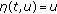 for all
for all  ,
,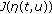 is non-increasing in
is non-increasing in 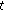 for any
for any 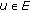 ,
,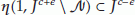 .
. . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  . Let
. Let  be a neighborhood of
be a neighborhood of 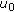 such that
such that 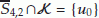 . By Lemma 3.3, there exists a critical point of mountain pass type
. By Lemma 3.3, there exists a critical point of mountain pass type 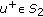 such that if
such that if  is a neighborhood of
is a neighborhood of 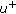 such that
such that  , then
, then 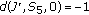 . Thus,
. Thus, 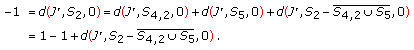
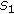 ,
, 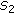 , and
, and 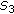 be as above. If
be as above. If 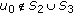 , the proof follows very closely that of the case (i).
, the proof follows very closely that of the case (i).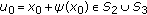 , hence
, hence  . Because
. Because 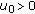 , there exists
, there exists  such that
such that 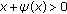 if
if  . So, if
. So, if 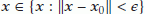 , then
, then  and
and 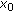 is a local maximum of
is a local maximum of 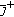 . Since we are assuming (1.1) to have only finitely many solutions,
. Since we are assuming (1.1) to have only finitely many solutions, 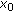 is a strictly local maximum of
is a strictly local maximum of 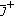 . Let
. Let 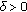 be such that
be such that 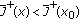 if
if  . Since
. Since 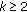 ,
,  is path connected. Thus,
is path connected. Thus,  is not a critical point of mountain pass type. By Lemma 3.3,
is not a critical point of mountain pass type. By Lemma 3.3,  has a critical point of mountain pass type
has a critical point of mountain pass type  . By (v) of Lemma 2.10,
. By (v) of Lemma 2.10,  , and hence
, and hence  . Let
. Let  be neighborhoods of
be neighborhoods of  and
and  , respectively, such that
, respectively, such that 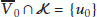 and
and 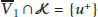 . Thus,
. Thus, 