- Research Article
- Open access
- Published:
Mixed Monotone Iterative Technique for Impulsive Periodic Boundary Value Problems in Banach Spaces
Boundary Value Problems volume 2011, Article number: 421261 (2011)
Abstract
This paper deals with the existence of  -quasi-solutions for impulsive periodic boundary value problems in an ordered Banach space
-quasi-solutions for impulsive periodic boundary value problems in an ordered Banach space  . Under a new concept of upper and lower solutions, a new monotone iterative technique on periodic boundary value problems of impulsive differential equations has been established. Our result improves and extends some relevant results in abstract differential equations.
. Under a new concept of upper and lower solutions, a new monotone iterative technique on periodic boundary value problems of impulsive differential equations has been established. Our result improves and extends some relevant results in abstract differential equations.
1. Introduction
The theory of impulsive differential equations is a new and important branch of differential equation theory, which has an extensive physical, chemical, biological, and engineering background and realistic mathematical model, and hence has been emerging as an important area of investigation in the last few decades; see [1]. Correspondingly, applications of the theory of impulsive differential equations to different areas were considered by many authors, and some basic results on impulsive differential equations have been obtained; see [2–5]. But many of them are about impulsive initial value problem; see [2, 3] and the references therein. The research on impulsive periodic boundary value problems is seldom; see [4, 5].
In this paper, we use a monotone iterative technique in the presence of coupled lower and upper  -quasisolutions to discuss the existence of solutions to the impulsive periodic boundary value problem (IPBVP) in an ordered Banach space
-quasisolutions to discuss the existence of solutions to the impulsive periodic boundary value problem (IPBVP) in an ordered Banach space 

where  ,
, ,
, ;
;  ;
;  is an impulsive function,
is an impulsive function,  .
.  denotes the jump of
denotes the jump of  at
at  that is,
that is,  where
where  and
and  represent the right and left limits of
represent the right and left limits of  at
at  , respectively.
, respectively.
The monotone iterative technique in the presence of lower and upper solutions is an important method for seeking solutions of differential equations in abstract spaces. Early on, Lakshmikantham and Leela [4] built a monotone iterative method for the periodic boundary value problem of first-order differential equation in 

and they proved that, if PBVP(1.2) has a lower solution  and an upper solution
and an upper solution  with
with  and nonlinear term
and nonlinear term  satisfies the monoton condition
satisfies the monoton condition

with a positive constant  , then PBVP(1.2) has minimal and maximal solutions between
, then PBVP(1.2) has minimal and maximal solutions between  and
and  which can be obtained by a monotone iterative procedure starting from
which can be obtained by a monotone iterative procedure starting from  and
and  , respectively. Later, He and Yu [5] developed the problem to impulsive differential equation
, respectively. Later, He and Yu [5] developed the problem to impulsive differential equation

where  ,
,  ,
,  ,
, 
But all of these results are in real spaces  We not only consider problems in Banach spaces, but also expand the nonlinear term to the case of
We not only consider problems in Banach spaces, but also expand the nonlinear term to the case of  If
If  is nondecreasing in
is nondecreasing in  and
and  is nonincreasing in
is nonincreasing in  then the monotonity condition (1.3) is not satisfied, and the results in [4, 5] are not right, in this case, we studied the IPBVP(1.1). As far as we know, no work has been done for the existence of solutions for IPBVP(1.1) in Banach spaces.
then the monotonity condition (1.3) is not satisfied, and the results in [4, 5] are not right, in this case, we studied the IPBVP(1.1). As far as we know, no work has been done for the existence of solutions for IPBVP(1.1) in Banach spaces.
In order to apply the monotone iterative technique to the initial value problem without impulse

Lakshmikantham et al. [6] and Guo and Lakshmikantham [7] obtained the existence of coupled quasisolutions of problem (1.5) by mixed monotone sequence of coupled quasiupper and lower solutions under the concept of quasiupper and lower solutions. In this paper, we improve and extend the above-mentioned results, and obtain the existence of the coupled minimal and maximal  -quasisolutions and the solutions between the coupled minimal and maximal
-quasisolutions and the solutions between the coupled minimal and maximal  -quasisolutions of the problem (1.1) through the mixed monotone iterative about the coupled
-quasisolutions of the problem (1.1) through the mixed monotone iterative about the coupled  -quasisolutions. If
-quasisolutions. If  the coupled upper and lower
the coupled upper and lower  -quasisolutions are equivalent to coupled upper and lower quasisolutions of the IPBVP(1.1). If
-quasisolutions are equivalent to coupled upper and lower quasisolutions of the IPBVP(1.1). If  ,
,  and
and  the coupled upper and lower
the coupled upper and lower  -quasisolutions are equivalent to upper and lower solutions of IPBVP(1.4).
-quasisolutions are equivalent to upper and lower solutions of IPBVP(1.4).
2. Preliminaries
Let  be an ordered Banach space with the norm
be an ordered Banach space with the norm  and partial order
and partial order  whose positive cone
whose positive cone  is normal with normal constant
is normal with normal constant  Let
Let  ,
,  is a constant;
is a constant;  ;
;  ,
,  ,
,  Let
Let  is continuous at
is continuous at  , and left continuous at
, and left continuous at  , and
, and  exists,
exists,  Evidently,
Evidently,  is a Banach space with the norm
is a Banach space with the norm  . An abstract function
. An abstract function  is called a solution of IPBVP(1.1) if
is called a solution of IPBVP(1.1) if  satisfies all the equalities of (1.1)
satisfies all the equalities of (1.1)
Let  and
and  exist,
exist,  . For
. For  it is easy to see that the left derivative
it is easy to see that the left derivative  of
of  at
at  exists and
exists and  and set
and set  , then
, then  If
If  is a solution of IPBVP(1.1), by the continuity of
is a solution of IPBVP(1.1), by the continuity of 
Let  denote the Banach space of all continuous
denote the Banach space of all continuous  -value functions on interval
-value functions on interval  with the norm
with the norm  . Let
. Let  denote the Kuratowski measure of noncompactness of the bounded set. For the details of the definition and properties of the measure of noncompactness, see [8]. For any
denote the Kuratowski measure of noncompactness of the bounded set. For the details of the definition and properties of the measure of noncompactness, see [8]. For any  and
and  set
set  If
If  is bounded in
is bounded in  then
then  is bounded in
is bounded in  and
and 
Now, we first give the following lemmas in order to prove our main results.
Lemma 2.1 (see [9]).
Let  be a bounded and countable set. Then
be a bounded and countable set. Then  is Lebesgue integral on
is Lebesgue integral on  and
and

Lemma 2.2 (see [10]).
Let  be bounded. Then exist a countable set
be bounded. Then exist a countable set  , such that
, such that 
Lemma 2.3 (see [11]).
Let  be equicontinuous. Then
be equicontinuous. Then  is continuous on
is continuous on  and
and

Lemma 2.4 (see [8]).
Let  be a Banach space and
be a Banach space and  is a bounded convex closed set in
is a bounded convex closed set in  be condensing, then
be condensing, then  has a fixed point in
has a fixed point in 
To prove our main results, for any  we consider the periodic boundary value problem (PBVP) of linear impulsive differential equation in
we consider the periodic boundary value problem (PBVP) of linear impulsive differential equation in 

where  ,
,  ,
, 
Lemma 2.5.
For any  ,
,  and
and  ,
,  the linear PBVP(2.3) has a unique solution
the linear PBVP(2.3) has a unique solution  given by
given by

where 
Proof.
For any  ,
,  and
and  ,
,  the linear initial value problem
the linear initial value problem

has a unique solution  given by
given by

where  is a constant [3].
is a constant [3].
If  is a solution of the linear initial value problem (2.5) satisfies
is a solution of the linear initial value problem (2.5) satisfies  namely
namely

then it is the solution of the linear PBVP(2.3). From (2.7), we have

So, (2.4) is satisfied.
Inversely, we can verify directly that the function  defined by (2.4) is a solution of the linear PBVP(2.3). Therefore, the conclusion of Lemma 2.5 holds.
defined by (2.4) is a solution of the linear PBVP(2.3). Therefore, the conclusion of Lemma 2.5 holds.
Definition 2.6.
Let  be a constant. If functions
be a constant. If functions  satisfy
satisfy


we call  ,
,  coupled lower and upper
coupled lower and upper  -quasisolutions of the IPBVP(1.1). Only choose "
-quasisolutions of the IPBVP(1.1). Only choose " " in (2.9) and (2.10), we call
" in (2.9) and (2.10), we call  coupled
coupled  -quasisolution pair of the IPBVP(1.1). Furthermore, if
-quasisolution pair of the IPBVP(1.1). Furthermore, if  we call
we call  a solution of the IPBVP(1.1).
a solution of the IPBVP(1.1).
Now, we define an operator  as following:
as following:

where

Evidently,  is also an ordered Banach space with the partial order "
is also an ordered Banach space with the partial order " " reduced by the positive cone
" reduced by the positive cone  .
.  is also normal with the same normal constant
is also normal with the same normal constant  . For
. For  with
with  we use
we use  to denote the order interval
to denote the order interval  in
in  and
and  to denote the order interval
to denote the order interval  in
in  .
.
3. Main Results
Theorem 3.1.
Let  be an ordered Banach space, whose positive cone
be an ordered Banach space, whose positive cone  is normal,
is normal,  and
and  ,
,  . Assume that the IPBVP(1.1) has coupled lower and upper
. Assume that the IPBVP(1.1) has coupled lower and upper  -quasisolutions
-quasisolutions  and
and  with
with  . Suppose that the following conditions are satisfied:
. Suppose that the following conditions are satisfied:
-
(H1)
There exist constants
 and
and 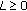 such that
such that (3.1)
(3.1)for any
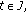 and
and 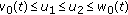 ,
, 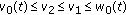 .
. -
(H2)
The impulsive function
 satisfies
satisfies (3.2)
(3.2)for any
 and
and 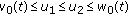 ,
, 
-
(H3)
There exist a constant
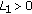 such that
such that (3.3)
(3.3)for all
 and increasing or decreasing monotonic sequences
and increasing or decreasing monotonic sequences 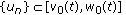 and
and 
-
(H4)
The sequences
 and
and 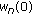 are convergent, where
are convergent, where  ,
, 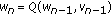 ,
, 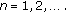
Then the IPBVP(1.1) has minimal and maximal coupled  -quasisolutions between
-quasisolutions between  and
and  which can be obtained by a monotone iterative procedure starting from
which can be obtained by a monotone iterative procedure starting from  and
and  , respectively.
, respectively.
Proof.
By the definition of  and Lemma 2.5,
and Lemma 2.5,  is continuous, and the coupled
is continuous, and the coupled  -quasisolutions of the IPBVP(1.1) is equivalent to the coupled fixed point of operator
-quasisolutions of the IPBVP(1.1) is equivalent to the coupled fixed point of operator  Combining this with the assumptions
Combining this with the assumptions  and
and  , we know
, we know  is a mixed monotone operator (about the mixed monotone operator, please see [6, 7]).
is a mixed monotone operator (about the mixed monotone operator, please see [6, 7]).
Next, we show  ,
,  . Let
. Let  by (2.9),
by (2.9),  and
and  ,
,  By Lemma 2.5
By Lemma 2.5

namely,  . Similarly, it can be show that
. Similarly, it can be show that  . So,
. So, 
Now, we define two sequences  and
and  in
in  by the iterative scheme
by the iterative scheme

Then from the mixed monotonicity of  , it follows that
, it follows that

We prove that  and
and  are uniformly convergent in
are uniformly convergent in 
For convenience, let  ,
,  ,
,  ,
,  and
and  . Since,
. Since,  and
and  by (2.11) and the boundedness of
by (2.11) and the boundedness of  and
and  we easy see that
we easy see that  and
and  is equicontinuous in every interval
is equicontinuous in every interval  so,
so,  is equicontinuous in every interval
is equicontinuous in every interval  where
where  ,
,  ,
,  From
From  and
and  it follows that
it follows that  and
and  for
for  Let
Let  ,
,  by Lemma 2.3,
by Lemma 2.3,  . Going from
. Going from  to
to  interval by interval we show that
interval by interval we show that  in
in 
For  from (2.11), using Lemma 2.1 and assumption
from (2.11), using Lemma 2.1 and assumption  and
and  we have
we have

Hence by the Belman inequality,  in
in  In particular,
In particular,  ,
,  this means that
this means that  and
and  are precompact in
are precompact in  Thus
Thus  and
and  are precompact in
are precompact in  and
and  ,
, 
Now, for  by (2.11) and the above argument for
by (2.11) and the above argument for  we have
we have

Again by Belman inequality,  in
in  from which we obtain that
from which we obtain that  ,
,  and
and  ,
, 
Continuing such a process interval by intervai up to  we can prove that
we can prove that  in every
in every  ,
, 
For any  if we modify the value of
if we modify the value of  ,
,  at
at  via
via  ,
,  ,
,  then
then  and it is equicontinuous. Since
and it is equicontinuous. Since  ,
,  is precompact in
is precompact in  for every
for every  By the Arzela-Ascoli theorem,
By the Arzela-Ascoli theorem,  is precompact in
is precompact in  Hence,
Hence,  has a convergent subsequence in
has a convergent subsequence in  Combining this with the monotonicity (3.6), we easily prove that
Combining this with the monotonicity (3.6), we easily prove that  itself is convergent in
itself is convergent in  In particular,
In particular,  is uniformly convergent over the whole of
is uniformly convergent over the whole of  Hence,
Hence,  is uniformly convergent in
is uniformly convergent in  Set
Set

Letting  in (3.5) and (3.6), we see that
in (3.5) and (3.6), we see that  and
and  ,
,  By the mixed monotonicity of
By the mixed monotonicity of  it is easy to see that
it is easy to see that  and
and  are the minimal and maximal coupled fixed points of
are the minimal and maximal coupled fixed points of  in
in  and therefore, they are the minimal and maximal coupled
and therefore, they are the minimal and maximal coupled  -quasisolutions of the IPBVP(1.1) in
-quasisolutions of the IPBVP(1.1) in  respectively.
respectively.
In Theorem 3.1, if  is weakly sequentially complete, condition
is weakly sequentially complete, condition  and
and  hold automatically. In fact, by Theorem
hold automatically. In fact, by Theorem  in [12], any monotonic and order-bounded sequence is precompact. By the monotonicity (3.6) and the same method in proof of Theorem 3.1, we can easily see that
in [12], any monotonic and order-bounded sequence is precompact. By the monotonicity (3.6) and the same method in proof of Theorem 3.1, we can easily see that  and
and  are convergent on
are convergent on  In particular,
In particular,  and
and  are convergent. So, condition
are convergent. So, condition  holds. Let
holds. Let  and
and  be increasing or decreasing sequences obeying condition
be increasing or decreasing sequences obeying condition  then by condition
then by condition  ,
,  is a monotonic and order-bounded sequence, so
is a monotonic and order-bounded sequence, so  Hence, condition
Hence, condition  holds. From Theorem 3.1, we obtain the following corollary.
holds. From Theorem 3.1, we obtain the following corollary.
Corollary 3.2.
Let  be an ordered and weakly sequentially complete Banach space, whose positive cone
be an ordered and weakly sequentially complete Banach space, whose positive cone  is normal,
is normal,  and
and  ,
,  If the IPBVP(1.1) has coupled lower and upper
If the IPBVP(1.1) has coupled lower and upper  -quasisolutions
-quasisolutions  and
and  with
with  and conditions
and conditions  and
and  are satisfied, then the IPBVP(1.1) has minimal and maximal coupled
are satisfied, then the IPBVP(1.1) has minimal and maximal coupled  -quasisolutions between
-quasisolutions between  and
and  which can be obtained by a monotone iterative procedure starting from
which can be obtained by a monotone iterative procedure starting from  and
and  respectively.
respectively.
If we replace the assumption  by the following assumption:
by the following assumption:
-
(H5)
There exist positive constants
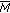 and
and 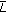 such that
such that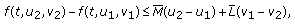 (3.10)
(3.10)for any
 and
and 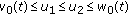 ,
, 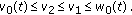
We have the following result.
Theorem 3.3.
Let  be an ordered Banach space, whose positive cone
be an ordered Banach space, whose positive cone  is normal,
is normal,  and
and  ,
,  If the IPBVP(1.1) has coupled lower and upper
If the IPBVP(1.1) has coupled lower and upper  -quasisolutions
-quasisolutions  and
and  with
with  and conditions
and conditions  ,
,  ,
,  and
and  hold, then the IPBVP(1.1) has minimal and maximal coupled
hold, then the IPBVP(1.1) has minimal and maximal coupled  -quasisolutions between
-quasisolutions between  and
and  which can be obtained by a monotone iterative procedure starting from
which can be obtained by a monotone iterative procedure starting from  and
and  respectively.
respectively.
Proof.
For  let
let  be a increasing sequence and
be a increasing sequence and be a decreasing sequence. For
be a decreasing sequence. For  with
with  by
by  and
and 

By this and the normality of cone  we have
we have

From this inequality and the definition of the measure noncompactness, it follows that

where  If
If  is a increasing sequence and
is a increasing sequence and  is a decreasing sequence, the above inequality is also valid. Hence
is a decreasing sequence, the above inequality is also valid. Hence  holds.
holds.
Therefore, by Theorem 3.1, the IPBVP(1.1) has minimal and maximal coupled  -quasisolutions between
-quasisolutions between  and
and  which can be obtained by a monotone iterative procedure starting from
which can be obtained by a monotone iterative procedure starting from  and
and  , respectively.
, respectively.
Now, we discuss the existence of the solution to the IPBVP(1.1) between the minimal and maximal coupled  -quasisolutions
-quasisolutions  and
and  If we replace the assumptions
If we replace the assumptions  and
and  by the following assumptions:
by the following assumptions:
The impulsive function  satisfies
satisfies

for any  and
and  ,
,  and there exist
and there exist  ,
,  such that
such that

for any countable sets  and
and  in
in 
There exist a constant  such that
such that

for any  where
where  and
and  are countable sets in
are countable sets in 
We have the following existence result.
Theorem 3.4.
Let  be an ordered Banach space, whose positive cone
be an ordered Banach space, whose positive cone  is normal,
is normal,  and
and  ,
,  If the IPBVP(1.1) has coupled lower and upper
If the IPBVP(1.1) has coupled lower and upper  -quasisolutions
-quasisolutions  and
and  with
with  such that assumptions
such that assumptions  ,
,  ,
,  and
and  hold, then the IPBVP(1.1) has minimal and maximal coupled
hold, then the IPBVP(1.1) has minimal and maximal coupled  -quasisolutions
-quasisolutions  and
and  between
between  and
and  and at least has one solution between
and at least has one solution between  and
and 
Proof.
We can easily see that  ,
,  Hence, by the Theorem 3.1, the IPBVP(1.1) has minimal and maximal coupled
Hence, by the Theorem 3.1, the IPBVP(1.1) has minimal and maximal coupled  -quasisolutions
-quasisolutions  and
and  between
between  and
and  Next, we prove the existence of the solution of the equation between
Next, we prove the existence of the solution of the equation between  and
and  Let
Let  clearly,
clearly,  is continuous and the solution of the IPBVP(1.1) is equivalent to the fixed point of operator
is continuous and the solution of the IPBVP(1.1) is equivalent to the fixed point of operator  Since
Since  is bounded and equicontinuous for any
is bounded and equicontinuous for any  by Lemma 2.2, there exist a countable set
by Lemma 2.2, there exist a countable set  such that
such that

By assumptions  and
and  and Lemma 2.1,
and Lemma 2.1,

Since  is equicontinuous, by Lemma 2.3,
is equicontinuous, by Lemma 2.3,  . Combing (3.17) and
. Combing (3.17) and  .
.
We have

Hence, the operator  is condensing, by the Lemma 2.4,
is condensing, by the Lemma 2.4,  has fixed point
has fixed point  in
in 
Lastly, since  ,
,  by the mixed monotonity of
by the mixed monotonity of 

Similarly,  in general,
in general,  letting
letting  we get
we get  Therefore, the IPBVP(1.1) at least has one solution between
Therefore, the IPBVP(1.1) at least has one solution between  and
and 
Remark 3.5.
If  and
and  then Theorems 3.1, 3.3 and 3.4 are generalizations of the main results of [5] in Banach spaces.
then Theorems 3.1, 3.3 and 3.4 are generalizations of the main results of [5] in Banach spaces.
Remark 3.6.
If  and
and  then Theorems 3.1, 3.3 and 3.4 are generalizations of the Theory
then Theorems 3.1, 3.3 and 3.4 are generalizations of the Theory  of [4] in Banach spaces.
of [4] in Banach spaces.
4. An Example
Consider the PBVP of infinite system for nonlinear impulsive differential equations:

4.1. Conclusion
IPBVP(4.1) has minimal and maximal coupled  -quasisolutions.
-quasisolutions.
Proof.
Let  ,
,  with norm
with norm  and
and  Then
Then  is a weakly sequentially complete Banach space and
is a weakly sequentially complete Banach space and  is normal cone in
is normal cone in  IPBVP(4.1) can be regarded as an PBVP of the form (1.1) in
IPBVP(4.1) can be regarded as an PBVP of the form (1.1) in  In this case,
In this case,  ,
,  ,
,  and
and  in which
in which

 ,
,  and
and  ,
, 
Evidently,  ,
,  Let
Let

 ,
,  Then it is easy to verify that
Then it is easy to verify that  ,
,  are coupled lower and upper
are coupled lower and upper  -quasisolutions of the IPBVP(4.1), and conditions
-quasisolutions of the IPBVP(4.1), and conditions  ,
,  hold. Hence, our conclusion follows from Corollary 3.2.
hold. Hence, our conclusion follows from Corollary 3.2.
References
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Guo DJ, Liu X: Extremal solutions of nonlinear impulsive integrodifferential equations in Banach spaces. Journal of Mathematical Analysis and Applications 1993, 177(2):538-552. 10.1006/jmaa.1993.1276
Li Y, Liu Z: Monotone iterative technique for addressing impulsive integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(1):83-92. 10.1016/j.na.2005.11.013
Lakshmikantham V, Leela S: Existence and monotone method for periodic solutions of first-order differential equations. Journal of Mathematical Analysis and Applications 1983, 91(1):237-243. 10.1016/0022-247X(83)90102-6
He Z, Yu J: Periodic boundary value problem for first-order impulsive ordinary differential equations. Journal of Mathematical Analysis and Applications 2002, 272(1):67-78. 10.1016/S0022-247X(02)00133-6
Lakshmikantham V, Leela S, Vatsala AS: Method of quasi-upper and lower solutions in abstract cones. Nonlinear Analysis 1982, 6(8):833-838. 10.1016/0362-546X(82)90067-0
Guo DJ, Lakshmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Analysis: Theory, Methods & Applications 1987, 11(5):623-632. 10.1016/0362-546X(87)90077-0
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Heinz H-P: On the behaviour of measures of noncompactness with respect to differentiation and integration of vector-valued functions. Nonlinear Analysis: Theory, Methods & Applications 1983, 7(12):1351-1371. 10.1016/0362-546X(83)90006-8
Li YX: Existence of solutions to initial value problems for abstract semilinear evolution equations. Acta Mathematica Sinica 2005, 48(6):1089-1094.
Guo DJ, Sun JX: Ordinary Differential Equations in Abstract Spaces. Shandong Science and Technology, Jinan, China; 1989.
Du YH: Fixed points of increasing operators in ordered Banach spaces and applications. Applicable Analysis 1990, 38(1-2):1-20. 10.1080/00036819008839957
Acknowledgments
This paper was supported by NNSF of China (10871160), the NSF of Gansu Province (0710RJZA103), and Project of NWNU-KJCXGC-3-47.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, P. Mixed Monotone Iterative Technique for Impulsive Periodic Boundary Value Problems in Banach Spaces. Bound Value Probl 2011, 421261 (2011). https://doi.org/10.1155/2011/421261
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/421261
 and
and 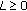 such that
such that
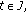 and
and 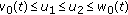 ,
, 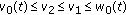 .
. satisfies
satisfies
 and
and 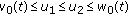 ,
, 
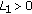 such that
such that
 and increasing or decreasing monotonic sequences
and increasing or decreasing monotonic sequences 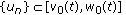 and
and 
 and
and 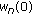 are convergent, where
are convergent, where  ,
, 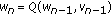 ,
, 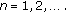
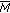 and
and 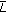 such that
such that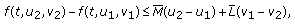
 and
and 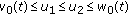 ,
,