- Research Article
- Open access
- Published:
New Fixed Point Theorems of Mixed Monotone Operators and Applications to Singular Boundary Value Problems on Time Scales
Boundary Value Problems volume 2011, Article number: 567054 (2011)
Abstract
Some new existence and uniqueness theorems of fixed points of mixed monotone operators are obtained, and then they are applied to a nonlinear singular second-order three-point boundary value problem on time scales. We prove the existence and uniqueness of a positive solution for the above problem which cannot be solved by using previously available methods.
1. Introduction
The study of mixed monotone operators has been a matter of discussion since they were introduced by Guo and Lakshmikantham [1] in 1987, because it has not only important theoretical meaning but also wide applications in microeconomics, the nuclear industry, and so on (see [1–4]). Recently, some new and interesting results about these kinds of operators have emerged, and they are used extensively in nonlinear differential and integral equations (see [5–9]).
In this paper, we extend the main results of [9] to mixed monotone operators. Without demanding compactness and continuity conditions and the existence of upper and lower solutions, we study the existence, uniqueness, and iterative convergence of fixed points of a class of mixed monotone operators. Then, we apply these results to the following singular second-order three-point boundary value problem on time scales:

where  with
with  ,
,  , and
, and  . The functions
. The functions  and
and  (
( ) are continuous. Our nonlinearity
) are continuous. Our nonlinearity  may have singularity at
may have singularity at  and/or
and/or  and
and  (
( ) may have singularity at
) may have singularity at  .
.
To understand the notations used in (1.1), we recall that  is a time scales, that is,
is a time scales, that is,  is an arbitrary nonempty closed subset of
is an arbitrary nonempty closed subset of  . For each interval
. For each interval  of
of  , we define
, we define  . For more details on time scales, one can refer to [10–12].
. For more details on time scales, one can refer to [10–12].
In recent years, there is much attention paid to the existence of positive solutions for nonlocal boundary value problems on time scales, see [13–18] and references therein. Dynamic equations have been applied in the study of insect population models, stock market and heat transfer and so on [19–22]. Time scales can be used in microeconomics models to study behavior which is sometimes continuous and sometimes discrete. A simple example of this continuous-discrete behavior is seen in suppliers short-run decisions and long-run decisions. Unifying both continuous and discrete model can avoid repeat research and has the capacity to get some different types of models which neither continuous models nor discrete models can effectively describe.
On the other hand, singular boundary value problems on time scales have also been investigated extensively (see [23–27]). We would like to mention some results of DaCunha et al. [23], Hao et al. [25], Luo [26], and Hu [27], which motivated us to consider problem (1.1).
In [23], DaCunha et al. considered the following singular second-order three-point dynamic boundary value problem:

where  is fixed and
is fixed and  is singular at
is singular at  and possible at
and possible at  ,
,  . The authors claimed that "we note that this is the first work (to our knowledge) that deals with singular boundary value problems in a general time scales setting." The results on existence of positive solutions were obtained by means of a fixed point theorem due to Gatica, Oliker and Waltman for mappings that are decreasing with respect to a cone.
. The authors claimed that "we note that this is the first work (to our knowledge) that deals with singular boundary value problems in a general time scales setting." The results on existence of positive solutions were obtained by means of a fixed point theorem due to Gatica, Oliker and Waltman for mappings that are decreasing with respect to a cone.
In [25], Hao et al. were concerned with the following singular boundary value problem of nonlinear dynamic equation

where  is rl-continuous and may be singular at
is rl-continuous and may be singular at  and/or
and/or  . With suitable growth and limit conditions, an existence theorem of positive solutions was established by using the Krasnoselskii fixed point theorem.
. With suitable growth and limit conditions, an existence theorem of positive solutions was established by using the Krasnoselskii fixed point theorem.
In [26], Luo studied the following singular  -point dynamic eigenvalue problem with mixed derivatives:
-point dynamic eigenvalue problem with mixed derivatives:

where  is singular at
is singular at  and
and  . The author obtained eigenvalue intervals in which there exists at least one positive solution of problem (1.4) by making use of the fixed point index theory.
. The author obtained eigenvalue intervals in which there exists at least one positive solution of problem (1.4) by making use of the fixed point index theory.
In [27], Hu were concerned with the following singular third-order three-point boundary value problem on time scales:

where  and
and  are continuous. The nonlinearity
are continuous. The nonlinearity  may have singularity at
may have singularity at  and/or
and/or  and
and  may have singularity at
may have singularity at  . With the aid of the fixed point theorem of cone expansion and compression type, results on the existence of positive solutions to (1.5) were obtained in the bounded set.
. With the aid of the fixed point theorem of cone expansion and compression type, results on the existence of positive solutions to (1.5) were obtained in the bounded set.
From the above research, we note that there is no result on the uniqueness of solutions and convergence of the iterative sequences for singular boundary value problems on time scales. As we know, completely continuity condition is crucial for the above discussion. However, it is difficult to verify for singular problems on time scales, in particular, in order to remove the singularity in  at
at  , more restricted conditions are required. For instance, condition
, more restricted conditions are required. For instance, condition  of Theorem 2.3 in [23] and condition
of Theorem 2.3 in [23] and condition  of Theorem 3.1 in [27]. In our abstract results on mixed monotone operators, since the compactness and continuity conditions are not required, they can be directly applied to singular boundary value problem (1.1).
of Theorem 3.1 in [27]. In our abstract results on mixed monotone operators, since the compactness and continuity conditions are not required, they can be directly applied to singular boundary value problem (1.1).
The purpose of this paper is to present some conditions for problem (1.1) that have a unique solution, the iterative sequences yielding approximate solutions are also given. Our main result generalizes and improves Theorem 2.3 in [18].
2. Preliminaries and Abstract Theorems
Let the real Banach space  be partially ordered by a cone
be partially ordered by a cone  of
of  , that is,
, that is,  if and only if
if and only if  .
.  is said to be a mixed monotone operator if
is said to be a mixed monotone operator if  is increasing in
is increasing in  and decreasing in
and decreasing in  , that is,
, that is,  ,
,  ,
,  implies
implies  . Element
. Element  is called a fixed point of
is called a fixed point of  if
if  .
.
Recall that cone  is said to be solid if the interior
is said to be solid if the interior  is nonempty and we denote
is nonempty and we denote  if
if  .
.  is said to be normal if there exists a positive constant
is said to be normal if there exists a positive constant  , such that
, such that  , the smallest
, the smallest  is called the normal constant of
is called the normal constant of  . For all
. For all  , the notation
, the notation  means that there exist
means that there exist  and
and  such that
such that  . Clearly, ~ is an equivalence relation. Given
. Clearly, ~ is an equivalence relation. Given  (i.e.,
(i.e.,  and
and  ), we denote by
), we denote by  the set
the set  . It is easy to see that
. It is easy to see that  is convex and
is convex and  for all
for all  . If
. If  and
and  , it is clear that
, it is clear that  .
.
All the concepts discussed above can be found in [1, 2, 4]. For more results about mixed monotone operators and other related concepts, the reader is referred to [3, 5–9] and some of the references therein.
In [9], Zhai and Cao introduced the following definition of  -
- -concave operators.
-concave operators.
Definition 2.1 (see [9]).
Let  be a real Banach space and
be a real Banach space and  be a cone in
be a cone in  . We say an operator
. We say an operator  is
is  -
- -concave if there exist two positive-valued functions
-concave if there exist two positive-valued functions  on interval
on interval  such that
such that
 is a surjection;
is a surjection;
 , for all
, for all  ;
;
 , for all
, for all  ,
,  .
.
They obtained the following result.
Theorem 2.2 (see [9]).
Let  be a real Banach space and
be a real Banach space and  be a normal cone in
be a normal cone in  . Suppose that an operator
. Suppose that an operator  is increasing and
is increasing and  -
- -concave. In addition, suppose that there exists
-concave. In addition, suppose that there exists  such that
such that  . Then
. Then
(i)there are  and
and  such that
such that  ,
,  ;
;
(ii)operator  has a unique fixed point
has a unique fixed point  in
in  ;
;
(iii)for any initial  , constructing successively the sequence
, constructing successively the sequence  ,
,  , we have
, we have  .
.
We can extend Theorem 2.2 to mixed monotone operators, our main results can be stated as follows.
Theorem 2.3.
Let  be a normal cone in a real Banach space
be a normal cone in a real Banach space  , and
, and  a mixed monotone operator. Assume that for all
a mixed monotone operator. Assume that for all  , there exist two positive-valued functions
, there exist two positive-valued functions  on interval
on interval  such that
such that
 is a surjection;
is a surjection;
 , for all
, for all  ;
;
 , for all
, for all  ,
,  .
.
In addition, suppose that there exists  such that
such that  . Then
. Then
(i)there are  and
and  such that
such that  ,
,  ;
;
(ii)operator  has a unique fixed point
has a unique fixed point  in
in  ;
;
(iii)for any initial  , constructing successively the sequences
, constructing successively the sequences  ,
,  ,
,  , we have
, we have  and
and  as
as  .
.
Corollary 2.4.
Let  be a real Banach space,
be a real Banach space,  a normal, solid cone in
a normal, solid cone in  . Suppose
. Suppose  is a mixed monotone operator and satisfies the conditions
is a mixed monotone operator and satisfies the conditions  of Theorem 2.3. Then
of Theorem 2.3. Then
(i)there are  and
and  such that
such that  ,
,  ;
;
(ii)operator  has a unique fixed point
has a unique fixed point  in
in  ;
;
(iii)for any initial  , constructing successively the sequences
, constructing successively the sequences  ,
,  ,
,  , we have
, we have  and
and  as
as  .
.
Remark 2.5.
In Theorem 2.3, if  with
with  is a solid cone, we can know that
is a solid cone, we can know that  is automatically satisfied. Therefore, we can deduce that Corollary 2.4 holds from Theorem 2.3. For simplicity, we only present the proof of Theorem 2.3.
is automatically satisfied. Therefore, we can deduce that Corollary 2.4 holds from Theorem 2.3. For simplicity, we only present the proof of Theorem 2.3.
Proof of Theorem 2.3.
Note that  , we can find a sufficiently small number
, we can find a sufficiently small number  such that
such that

According to  , we can obtain that there exists
, we can obtain that there exists  such that
such that  , thus
, thus

Since  , we can find a positive integer
, we can find a positive integer  such that
such that

Let  ,
,  , and construct successively the sequences
, and construct successively the sequences

It is clear that  and
and  ,
,  . In general, we obtain
. In general, we obtain  ,
,  .
.
It follows from  , (2.2), and (2.3) that
, (2.2), and (2.3) that

From  , we have
, we have

Combining (2.2) with (2.3) and (2.6), we have

Thus, we obtain

By induction, it is easy to obtain that

Take any  , then
, then  and
and  . So we can know that
. So we can know that

Let

Thus, we have  ,
,  , and then
, and then

Therefore,  ; that is,
; that is,

Set  , we will show that
, we will show that  . In fact, if
. In fact, if  , by
, by  , there exists
, there exists  such that
such that  . Consider the following two cases.
. Consider the following two cases.
-
(i)
There exists an integer
 such that
such that 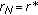 . In this case, we have
. In this case, we have  and
and 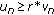 for all
for all 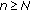 hold. Hence
hold. Hence 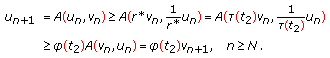 (2.14)
(2.14)
By the definition of  , we have
, we have

which is a contradiction.
-
(ii)
For all integers
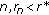 . Then, we obtain
. Then, we obtain 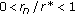 . By
. By 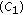 , there exist
, there exist 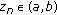 such that
such that 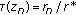 . Hence
. Hence 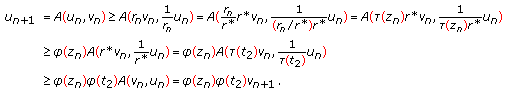 (2.16)
(2.16)
By the definition of  , we have
, we have

Let  , we have
, we have

which is also a contradiction. Thus,  .
.
Furthermore, similarly to the proof of Theorem 2.1 in [9], there exits  such that
such that  , and
, and  is the fixed point of operator
is the fixed point of operator  .
.
In the following, we prove that  is the unique fixed point of
is the unique fixed point of  in
in  . In fact, suppose that
. In fact, suppose that  is another fixed point of operator
is another fixed point of operator  . Let
. Let

Clearly,  and
and  . If
. If  , according to
, according to  , there exists
, there exists  such that
such that  . Then
. Then

It follows that

Hence,  , which is a contradiction. Thus we have
, which is a contradiction. Thus we have  , that is,
, that is,  . Therefore,
. Therefore,  has a unique fixed point
has a unique fixed point  in
in  . Note that
. Note that  , so we know that
, so we know that  is the unique fixed point of
is the unique fixed point of  in
in  . For any initial
. For any initial  , we can choose a small number
, we can choose a small number  such that
such that

From  , there is
, there is  such that
such that  , thus
, thus

We can choose a sufficiently large positive integer  such that
such that

Take  ,
,  . We can find that
. We can find that

constructing successively the sequences

By using the mixed monotone properties of operator  , we have
, we have

Similarly to the above proof, we can know that there exists  such that
such that

By the uniqueness of fixed points of operator  in
in  , we have
, we have  . Taking into account that
. Taking into account that  is normal, we deduce that
is normal, we deduce that  . This completes the proof.
. This completes the proof.
3. Applications to Singular BVP (1.1) on Time Scales
A Banach space  is the set of real-valued continuous (in the topology of
is the set of real-valued continuous (in the topology of  ) function
) function  defined on
defined on  with the norm
with the norm  .
.
Define a cone by

It is clear that  is a normal cone of which the normality constant is 1.
is a normal cone of which the normality constant is 1.
In order to obtain our main result, we need the following lemmas.
Lemma 3.1 (see [18]).
The Green function corresponding to the following problem

is given by

where

is Green's function for the BVP:

Lemma 3.2 (see [18]).
For any  , we have
, we have

Our main result is the following theorem.
Theorem 3.3.
Assume that
 is nondecreasing,
is nondecreasing,  is nonincreasing and there exist
is nonincreasing and there exist  on interval
on interval  such that
such that  is a surjection and
is a surjection and  , for all
, for all  which satisfy
which satisfy

there exist two constants  and
and  such that
such that

Then problem (1.1) has a unique positive solution  in
in  . Moreover, for any initial
. Moreover, for any initial  , constructing successively the sequences
, constructing successively the sequences

we have  and
and  as
as  .
.
Proof of Theorem 3.3.
Define an operator 

It is easy to check that  is a solution of problem (1.1) if and only if
is a solution of problem (1.1) if and only if  is a fixed point of operator
is a fixed point of operator  . Clearly, we can know that
. Clearly, we can know that  is a mixed monotone operator. For any
is a mixed monotone operator. For any  and
and  , according to
, according to  , we obtain
, we obtain

Hence,

In addition, from  , we know that
, we know that

Thus  . Therefore, all the conditions of Theorem 2.3 are satisfied. By Theorem 2.3, we can obtain the conclusions of Theorem 3.3.
. Therefore, all the conditions of Theorem 2.3 are satisfied. By Theorem 2.3, we can obtain the conclusions of Theorem 3.3.
Now, let us end this paper by the following example.
Example 3.4.
Let  , consider the following BVP on time scales
, consider the following BVP on time scales

Set  ,
,  ,
,  ,
,  ,
,  . Then
. Then  is a surjection and
is a surjection and  for
for  .
.
For any  ,
,  , it is easy to check that
, it is easy to check that

It follows from Lemma 3.1 that

Let  , since
, since

We choose  , according to Lemma 3.2, we have
, according to Lemma 3.2, we have

By Theorem 3.3, problem (3.14) has a unique positive solution  in
in  . For any initial
. For any initial  , constructing successively the sequences
, constructing successively the sequences

we have  as
as  .
.
Remark 3.5.
Example 3.4 indicates that Theorem 3.3 generalizes and complements Theorem 2.3 in [18] at the following aspects. Firstly, in our proof, we only need to check the conditions "there exists  such that
such that  ", in fact, the author has shown that "
", in fact, the author has shown that " " in the proof of Theorem 2.3 in [18]. It is clear that our hypotheses are weaker than those imposed in Theorem 2.3 in [18]. According to Lemma 3.2, we can know that the condition
" in the proof of Theorem 2.3 in [18]. It is clear that our hypotheses are weaker than those imposed in Theorem 2.3 in [18]. According to Lemma 3.2, we can know that the condition  is automatically satisfied. Secondly, we have considered the case that the condition "
is automatically satisfied. Secondly, we have considered the case that the condition " and
and  (
( )" is not satisfied, therefore, the condition
)" is not satisfied, therefore, the condition  incorporates the more comprehensive functions than the condition
incorporates the more comprehensive functions than the condition  in Theorem 2.3 in [18]. Thirdly, the more general conditions are imposed on our nonlinear term, they can be the sum of nondecreasing functions and nonincreasing functions.
in Theorem 2.3 in [18]. Thirdly, the more general conditions are imposed on our nonlinear term, they can be the sum of nondecreasing functions and nonincreasing functions.
References
Guo D, Lakshmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Analysis: Theory, Methods & Applications 1987, 11(5):623-632. 10.1016/0362-546X(87)90077-0
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Zhao ZQ: Existence and uniqueness of fixed points of some mixed monotone mappings in partially ordered linear spaces. Journal of Systems Science and Mathematical Sciences 1999, 19(2):217-224.
Guo DJ: Partial Order Methods in Nonlinear Analysis. Shandong Science and Technology Press, Jinan, China; 2000.
Wu YX, Liang ZD: Existence and uniqueness of fixed points for mixed monotone operators with applications. Nonlinear Analysis: Theory, Methods & Applications 2006, 65(10):1913-1924. 10.1016/j.na.2005.10.045
Drici Z, McRae FA, Devi JV: Fixed point theorems for mixed monotone operators with PPF dependence. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(2):632-636. 10.1016/j.na.2007.05.044
Zhang Z, Wang K: On fixed point theorems of mixed monotone operators and applications. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3279-3284. 10.1016/j.na.2008.04.032
Zhao ZQ: Existence and uniqueness of fixed points for some mixed monotone operators. Nonlinear Analysis: Theory, Methods & Applications 2010, 73(6):1481-1490. 10.1016/j.na.2010.04.008
Zhai C-B, Cao X-M:Fixed point theorems for
 -
- -concave operators and applications. Computers & Mathematics with Applications 2010, 59(1):532-538. 10.1016/j.camwa.2009.06.016
-concave operators and applications. Computers & Mathematics with Applications 2010, 59(1):532-538. 10.1016/j.camwa.2009.06.016Atici FM, Guseinov GS: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002, 141(1-2):75-99. 10.1016/S0377-0427(01)00437-X
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Anderson DR: Solutions to second-order three-point problems on time scales. Journal of Difference Equations and Applications 2002, 8(8):673-688. 10.1080/1023619021000000717
Anderson DR, Wong PJY: Positive solutions for second-order semipositone problems on time scales. Computers & Mathematics with Applications 2009, 58(2):281-291. 10.1016/j.camwa.2009.02.033
Anderson DR, Zhai C: Positive solutions to semi-positone second-order three-point problems on time scales. Applied Mathematics and Computation 2010, 215(10):3713-3720. 10.1016/j.amc.2009.11.010
Kaufmann ER: Positive solutions of a three-point boundary-value problem on a time scale. Electronic Journal of Differential Equations 2003, 82: 1-11.
Hamal NA, Yoruk F: Positive solutions of nonlinear m -point boundary value problems on time scales. Journal of Computational and Applied Mathematics 2009, 231(1):92-105. 10.1016/j.cam.2009.02.003
Sun J-P: Existence of positive solution to second-order three-point BVPs on time scales. Boundary Value Problems 2009, 2009:-6.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics. Resultate der Mathematik 1990, 18(1-2):18-56.
Jamieson V, Spedding V: Taming nature's numbers. New Scientist: The Global Science and Technology Weekly 2003, 2404: 28-31.
Atici FM, Biles DC, Lebedinsky A: An application of time scales to economics. Mathematical and Computer Modelling 2006, 43(7-8):718-726. 10.1016/j.mcm.2005.08.014
Tisdell CC, Zaidi A: Basic qualitative and quantitative results for solutions to nonlinear, dynamic equations on time scales with an application to economic modelling. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(11):3504-3524. 10.1016/j.na.2007.03.043
DaCunha JJ, Davis JM, Singh PK: Existence results for singular three point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004, 295(2):378-391. 10.1016/j.jmaa.2004.02.049
Bohner M, Luo H: Singular second-order multipoint dynamic boundary value problems with mixed derivatives. Advances in Difference Equations 2006, 2006:-15.
Hao Z-C, Xiao T-J, Liang J: Existence of positive solutions for singular boundary value problem on time scales. Journal of Mathematical Analysis and Applications 2007, 325(1):517-528. 10.1016/j.jmaa.2006.01.083
Luo H: Positive solutions to singular multi-point dynamic eigenvalue problems with mixed derivatives. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(4):1679-1691. 10.1016/j.na.2008.02.051
Hu LG: Positive solutions to singular third-order three-point boundary value problems on time scales. Mathematical and Computer Modelling 2010, 51(5-6):606-615.
Acknowledgment
H. Xu was supported financially by the Science Foundation of North University of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, H. New Fixed Point Theorems of Mixed Monotone Operators and Applications to Singular Boundary Value Problems on Time Scales. Bound Value Probl 2011, 567054 (2011). https://doi.org/10.1155/2011/567054
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/567054
 such that
such that 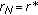 . In this case, we have
. In this case, we have  and
and 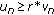 for all
for all 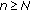 hold. Hence
hold. Hence 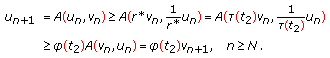
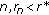 . Then, we obtain
. Then, we obtain 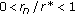 . By
. By 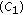 , there exist
, there exist 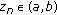 such that
such that 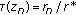 . Hence
. Hence 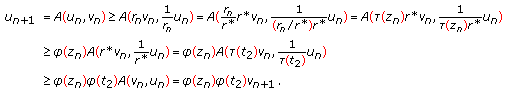
 -
- -concave operators and applications. Computers & Mathematics with Applications 2010, 59(1):532-538. 10.1016/j.camwa.2009.06.016
-concave operators and applications. Computers & Mathematics with Applications 2010, 59(1):532-538. 10.1016/j.camwa.2009.06.016