- Research Article
- Open access
- Published:
Eigenvalue Problem and Unbounded Connected Branch of Positive Solutions to a Class of Singular Elastic Beam Equations
Boundary Value Problems volume 2011, Article number: 594128 (2011)
Abstract
This paper investigates the eigenvalue problem for a class of singular elastic beam equations where one end is simply supported and the other end is clamped by sliding clamps. Firstly, we establish a necessary and sufficient condition for the existence of positive solutions, then we prove that the closure of positive solution set possesses an unbounded connected branch which bifurcates from  Our nonlinearity
Our nonlinearity  may be singular at
may be singular at  and/or
and/or  .
.
1. Introduction
Singular differential equations arise in the fields of gas dynamics, Newtonian fluid mechanics, the theory of boundary layer, and so on. Therefore, singular boundary value problems have been investigated extensively in recent years (see [1–4] and references therein).
This paper investigates the following fourth-order nonlinear singular eigenvalue problem:

where  is a parameter and
is a parameter and  satisfies the following hypothesis:
satisfies the following hypothesis:
() , and there exist constants
, and there exist constants  ,
,  ,
,  ,
,  ,
, such that for any
such that for any  ,
,  ,
,  satisfies
satisfies

Typical functions that satisfy the above sublinear hypothesis ( ) are those taking the form
) are those taking the form

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . The hypothesis (
. The hypothesis ( ) is similar to that in [5, 6].
) is similar to that in [5, 6].
Because of the extensive applications in mechanics and engineering, nonlinear fourth-order two-point boundary value problems have received wide attentions (see [7–12] and references therein). In mechanics, the boundary value problem (1.1) (BVP (1.1) for short) describes the deformation of an elastic beam simply supported at left and clamped at right by sliding clamps. The term  in
in  represents bending effect which is useful for the stability analysis of the beam. BVP (1.1) has two special features. The first one is that the nonlinearity
represents bending effect which is useful for the stability analysis of the beam. BVP (1.1) has two special features. The first one is that the nonlinearity  may depend on the first-order derivative of the unknown function
may depend on the first-order derivative of the unknown function  , and the second one is that the nonlinearity
, and the second one is that the nonlinearity  may be singular at
may be singular at  and/or
and/or  .
.
In this paper, we study the existence of positive solutions and the structure of positive solution set for the BVP (1.1). Firstly, we construct a special cone and present a necessary and sufficient condition for the existence of positive solutions, then we prove that the closure of positive solution set possesses an unbounded connected branch which bifurcates from  . Our analysis mainly relies on the fixed point theorem in a cone and the fixed point index theory.
. Our analysis mainly relies on the fixed point theorem in a cone and the fixed point index theory.
By singularity of  , we mean that the function
, we mean that the function  in (1.1) is allowed to be unbounded at the points
in (1.1) is allowed to be unbounded at the points  ,
,  ,
,  , and/or
, and/or  . A function
. A function  is called a (positive) solution of the BVP (1.1) if it satisfies the BVP (1.1) (
is called a (positive) solution of the BVP (1.1) if it satisfies the BVP (1.1) ( for
for  and
and  for
for  ). For some
). For some  , if the
, if the  (1.1) has a positive solution
(1.1) has a positive solution  , then
, then  is called an eigenvalue and
is called an eigenvalue and  is called corresponding eigenfunction of the BVP (1.1).
is called corresponding eigenfunction of the BVP (1.1).
The existence of positive solutions of BVPs has been studied by several authors in the literature; for example, see [7–20] and the references therein. Yao [15, 18] studied the following BVP:

where  is a closed subset and
is a closed subset and  ,
,  . In [15], he obtained a sufficient condition for the existence of positive solutions of
. In [15], he obtained a sufficient condition for the existence of positive solutions of  (1.4) by using the monotonically iterative technique. In [13, 18], he applied Guo-Krasnosel'skii's fixed point theorem to obtain the existence and multiplicity of positive solutions of BVP (1.4) and the following BVP:
(1.4) by using the monotonically iterative technique. In [13, 18], he applied Guo-Krasnosel'skii's fixed point theorem to obtain the existence and multiplicity of positive solutions of BVP (1.4) and the following BVP:

These differ from our problem because  in (1.4) cannot be singular at
in (1.4) cannot be singular at  ,
,  and the nonlinearity
and the nonlinearity  in (1.5) does not depend on the derivatives of the unknown functions.
in (1.5) does not depend on the derivatives of the unknown functions.
In this paper, we first establish a necessary and sufficient condition for the existence of positive solutions of BVP (1.1) for any  by using the following Lemma 1.1. Efforts to obtain necessary and sufficient conditions for the existence of positive solutions of BVPs by the lower and upper solution method can be found, for example, in [5, 6, 21–23]. In [5, 6, 22, 23] they considered the case that
by using the following Lemma 1.1. Efforts to obtain necessary and sufficient conditions for the existence of positive solutions of BVPs by the lower and upper solution method can be found, for example, in [5, 6, 21–23]. In [5, 6, 22, 23] they considered the case that  depends on even order derivatives of
depends on even order derivatives of  . Although the nonlinearity
. Although the nonlinearity  in [21] depends on the first-order derivative, where the nonlinearity
in [21] depends on the first-order derivative, where the nonlinearity  is increasing with respect to the unknown function
is increasing with respect to the unknown function  . Papers [24, 25] derived the existence of positive solutions of BVPs by the lower and upper solution method, but the nonlinearity
. Papers [24, 25] derived the existence of positive solutions of BVPs by the lower and upper solution method, but the nonlinearity  does not depend on the derivatives of the unknown functions, and
does not depend on the derivatives of the unknown functions, and  is decreasing with respect to
is decreasing with respect to  .
.
Recently, the global structure of positive solutions of nonlinear boundary value problems has also been investigated (see [26–28] and references therein). Ma and An [26] and Ma and Xu [27] discussed the global structure of positive solutions for the nonlinear eigenvalue problems and obtained the existence of an unbounded connected branch of positive solution set by using global bifurcation theorems (see [29, 30]). The terms  in [26] and
in [26] and  in [27] are not singular at
in [27] are not singular at  ,
,  ,
,  . Yao [14] obtained one or two positive solutions to a singular elastic beam equation rigidly fixed at both ends by using Guo-Krasnosel'skii's fixed point theorem, but the global structure of positive solutions was not considered. Since the nonlinearity
. Yao [14] obtained one or two positive solutions to a singular elastic beam equation rigidly fixed at both ends by using Guo-Krasnosel'skii's fixed point theorem, but the global structure of positive solutions was not considered. Since the nonlinearity  in BVP (1.1) may be singular at
in BVP (1.1) may be singular at  and/or
and/or  , the global bifurcation theorems in [29, 30] do not apply to our problem here. In Section 4, we also investigate the global structure of positive solutions for BVP (1.1) by applying the following Lemma 1.2.
, the global bifurcation theorems in [29, 30] do not apply to our problem here. In Section 4, we also investigate the global structure of positive solutions for BVP (1.1) by applying the following Lemma 1.2.
The paper is organized as follows: in the rest of this section, two known results are stated. In Section 2, some lemmas are stated and proved. In Section 3, we establish a necessary and sufficient condition for the existence of positive solutions. In Section 4, we prove that the closure of positive solution set possesses an unbounded connected branch which comes from  .
.
Finally we state the following results which will be used in Sections 3 and 4, respectively.
Lemma 1.1 (see [31]).
Let  be a real Banach space, let
be a real Banach space, let  be a cone in
be a cone in  , and let
, and let  ,
,  be bounded open sets of
be bounded open sets of  ,
, . Suppose that
. Suppose that  is completely continuous such that one of the following two conditions is satisfied:
is completely continuous such that one of the following two conditions is satisfied:

Then,  has a fixed point in
has a fixed point in  .
.
Lemma 1.2 (see [32]).
Let  be a metric space and
be a metric space and  . Let
. Let  and
and  satisfy
satisfy

Suppose also that  is a family of connected subsets of
is a family of connected subsets of  , satisfying the following conditions:
, satisfying the following conditions:
 and
and  for each
for each  .
.
(2)For any two given numbers  and
and  with
with  ,
,  is a relatively compact set of
is a relatively compact set of  .
.
Then there exists a connected branch  of
of  such that
such that

where  there exists a sequence
there exists a sequence  such that
such that  .
.
2. Some Preliminaries and Lemmas
Let  ,
,  , then
, then  is a Banach space, where
is a Banach space, where  Define
Define

It is easy to conclude that  is a cone of
is a cone of  . Denote
. Denote

Let

Then  is the Green function of homogeneous boundary value problem
is the Green function of homogeneous boundary value problem

Lemma 2.1.
 ,
,  , and
, and  have the following properties:
have the following properties:
(1) ,
,  ,
,  , for all
, for all  .
.
(2) ,
,  ,
,  (or
(or  ), for all
), for all  .
.
(3) ,
,  ,
,  , for all
, for all  .
.
(4) ,
,  ,
,  , for all
, for all  .
.
Proof.
From (2.4), it is easy to obtain the property (2.18).
We now prove that property (2) is true. For  , by (2.4), we have
, by (2.4), we have

For  , by (2.4), we have
, by (2.4), we have

Consequently, property (2) holds.
From property (2), it is easy to obtain property (3).
We next show that property (4) is true. From (2.4), we know that property (4) holds for  .
.
For  , if
, if  , then
, then

if  , then
, then

Therefore, property (4) holds.
Lemma 2.2.
Assume that  , then
, then  and
and


Proof.
Assume that  , then
, then  ,
,  ,
,  , so
, so

Therefore, (2.9) holds. From (2.9), we get

By (2.9) and the definition of  , we can obtain that
, we can obtain that

Thus, (2.10) holds.
For any fixed  , define an operator
, define an operator  by
by

Then, it is easy to know that


Lemma 2.3.
Suppose that ( ) and
) and

hold. Then  .
.
Proof.
From ( ), for any
), for any  ,
,  ,
,  , we easily obtain the following inequalities:
, we easily obtain the following inequalities:

For every  ,
,  , choose positive numbers
, choose positive numbers  min
min  . It follows from (
. It follows from ( ), (2.10), Lemma 2.1, and (2.17) that
), (2.10), Lemma 2.1, and (2.17) that

Similar to (2.19), from ( ), (2.10), Lemma 2.1, and (2.17), for every
), (2.10), Lemma 2.1, and (2.17), for every  ,
,  , we have
, we have

Thus,  is well defined on
is well defined on  .
.
From (2.4) and (2.14)–(2.16), it is easy to know that

Therefore,  follows from (2.21).
follows from (2.21).
Obviously,  is a positive solution of BVP (1.1) if and only if
is a positive solution of BVP (1.1) if and only if  is a positive fixed point of the integral operator
is a positive fixed point of the integral operator  in
in  .
.
Lemma 2.4.
Suppose that ( ) and (2.17) hold. Then for any
) and (2.17) hold. Then for any  ,
,  is completely continuous.
is completely continuous.
Proof.
First of all, notice that  maps
maps  into
into  by Lemma 2.3.
by Lemma 2.3.
Next, we show that  is bounded. In fact, for any
is bounded. In fact, for any  , by (2.10) we can get
, by (2.10) we can get

Choose positive numbers  ,
,  ,
,  . This, together with (
. This, together with ( ), (2.22), (2.16), and Lemma 2.1 yields that
), (2.22), (2.16), and Lemma 2.1 yields that

Thus,  is bounded on
is bounded on  .
.
Now we show that  is a compact operator on
is a compact operator on  . By (2.23) and Ascoli-Arzela theorem, it suffices to show that
. By (2.23) and Ascoli-Arzela theorem, it suffices to show that  is equicontinuous for arbitrary bounded subset
is equicontinuous for arbitrary bounded subset  .
.
Since for each  , (2.22) holds, we may choose still positive numbers
, (2.22) holds, we may choose still positive numbers  ,
,  ,
,  . Then
. Then

where  . Notice that
. Notice that

Thus for any given  with
with  and for any
and for any  , we get
, we get

From (2.25), (2.26), and the absolute continuity of integral function, it follows that  is equicontinuous.
is equicontinuous.
Therefore,  is relatively compact, that is,
is relatively compact, that is,  is a compact operator on
is a compact operator on  .
.
Finally, we show that  is continuous on
is continuous on  . Suppose
. Suppose  ,
,  and
and  . Then
. Then  ,
, and
and  as
as  uniformly, with respect to
uniformly, with respect to  . From
. From  , choose still positive numbers
, choose still positive numbers  ,
,  ,
,  . Then
. Then

By (2.17), we know that  is integrable on
is integrable on  . Thus, from the Lebesgue dominated convergence theorem, it follows that
. Thus, from the Lebesgue dominated convergence theorem, it follows that

Thus,  is continuous on
is continuous on  . Therefore,
. Therefore,  is completely continuous.
is completely continuous.
3. A Necessary and Sufficient Condition for Existence of Positive Solutions
In this section, by using the fixed point theorem of cone, we establish the following necessary and sufficient condition for the existence of positive solutions for BVP (1.1).
Theorem 3.1.
Suppose ( ) holds, then BVP (1.1) has at least one positive solution for any
) holds, then BVP (1.1) has at least one positive solution for any  if and only if the integral inequality (2.17) holds.
if and only if the integral inequality (2.17) holds.
Proof.
Suppose first that  be a positive solution of BVP (1.1) for any fixed
be a positive solution of BVP (1.1) for any fixed  . Then there exist constants
. Then there exist constants  (
( ) with
) with  ,
,  such that
such that

In fact, it follows from  ,
,  and
and  , that
, that  for
for  and
and  ,
,  for
for  . By the concavity of
. By the concavity of  and
and  , we have
, we have

On the other hand,

Let  let
let and let
and let then (3.1) holds.
then (3.1) holds.
Choose positive numbers  ,
,  ,
,  . This, together with (
. This, together with ( ), (1.2), and (2.18) yields that
), (1.2), and (2.18) yields that

where  . Hence, integrating (3.4) from
. Hence, integrating (3.4) from  to 1, we obtain
to 1, we obtain

Since  increases on
increases on  , we get
, we get

that is,

Notice that  , integrating (3.7) from 0 to 1, we have
, integrating (3.7) from 0 to 1, we have

That is,

Thus,

By an argument similar to the one used in deriving (3.5), we can obtain

where  . So,
. So,

Integrating (3.12) from 0 to 1, we have

That is,

So,

This and (3.10) imply that (2.17) holds.
Now assume that (2.17) holds, we will show that BVP (1.1) has at least one positive solution for any  . By (2.17), there exists a sufficient small
. By (2.17), there exists a sufficient small  such that
such that

For any fixed  , first of all, we prove
, first of all, we prove

where  .
.
Let  , then
, then

From Lemma 2.1, (3.18), and ( ), we get
), we get

Thus, (3.17) holds.
Next, we claim that

where  .
.
Let  , then for
, then for  , we get
, we get

Therefore, by Lemma 2.1 and ( ), it follows that
), it follows that

This implies that (3.20) holds.
By Lemmas 1.1 and 2.4, (3.17), and (3.20), we obtain that  has a fixed point in
has a fixed point in  . Therefore, BVP (1.1) has a positive solution in
. Therefore, BVP (1.1) has a positive solution in  for any
for any  .
.
4. Unbounded Connected Branch of Positive Solutions
In this section, we study the global continua results under the hypotheses ( ) and (2.17). Let
) and (2.17). Let

then, by Theorem 3.1,  for any
for any  .
.
Theorem 4.1.
Suppose ( ) and (2.17) hold, then the closure
) and (2.17) hold, then the closure  of positive solution set possesses an unbounded connected branch
of positive solution set possesses an unbounded connected branch  which comes from
which comes from  such that
such that
(i)for any  , and
, and
(ii)
Proof.
We now prove our conclusion by the following several steps.
First, we prove that for arbitrarily given  is bounded. In fact, let
is bounded. In fact, let

then for  and
and  , we get
, we get

Therefore, by Lemma 2.1 and ( ), it follows that
), it follows that

Let

where  is given by (3.16). Then for
is given by (3.16). Then for  and
and  , we get
, we get

Therefore, by Lemma 2.1 and ( ), it follows that
), it follows that

Therefore,  has no positive solution in
has no positive solution in  . As a consequence,
. As a consequence,  is bounded.
is bounded.
By the complete continuity of  ,
,  is compact.
is compact.
Second, we choose sequences  and
and  satisfy
satisfy

We are to prove that for any positive integer  , there exists a connected branch
, there exists a connected branch  of
of  satisfying
satisfying

Let  be fixed, suppose that for any
be fixed, suppose that for any  , the connected branch
, the connected branch  of
of  , passing through
, passing through  , leads to
, leads to  . Since
. Since  is compact, there exists a bounded open subset
is compact, there exists a bounded open subset  of
of  such that
such that  ,
,  , and
, and  , where
, where  and later
and later  denote the closure and boundary of
denote the closure and boundary of  with respect to
with respect to  . If
. If  , then
, then  and
and  are two disjoint closed subsets of
are two disjoint closed subsets of  . Since
. Since  is a compact metric space, there are two disjoint compact subsets
is a compact metric space, there are two disjoint compact subsets  and
and  of
of  such that
such that  ,
,  , and
, and  . Evidently,
. Evidently,  . Denoting by
. Denoting by  the
the  -neighborhood of
-neighborhood of  and letting
and letting  , then it follows that
, then it follows that

If  , then taking
, then taking  .
.
It is obvious that in  , the family of
, the family of  makes up an open covering of
makes up an open covering of  . Since
. Since  is a compact set, there exists a finite subfamily
is a compact set, there exists a finite subfamily  which also covers
which also covers  . Let
. Let  , then
, then

Hence, by the homotopy invariance of the fixed point index, we obtain

By the first step of this proof, the construction of  , (4.4), and (4.7), it follows easily that there exist
, (4.4), and (4.7), it follows easily that there exist  such that
such that



However, by the excision property and additivity of the fixed point index, we have from (4.12) and (4.14) that  , which contradicts (4.15). Hence, there exists some
, which contradicts (4.15). Hence, there exists some  such that the connected branch
such that the connected branch  of
of  containing
containing  satisfies that
satisfies that  . Let
. Let  be the connected branch of
be the connected branch of  including
including  , then this
, then this  satisfies (4.9).
satisfies (4.9).
By Lemma 1.2, there exists a connected branch  of
of  such that
such that  for any
for any  . Noticing
. Noticing  , we have
, we have  . Let
. Let  be the connected branch of
be the connected branch of  including
including  , then
, then  for any
for any  . Similar to (4.4) and (4.7), for any
. Similar to (4.4) and (4.7), for any  ,
,  , we have, by (
, we have, by ( ), (4.2), (4.3), (4.5), (4.6), and Lemma 2.1,
), (4.2), (4.3), (4.5), (4.6), and Lemma 2.1,


where  is given by (3.16). Let
is given by (3.16). Let  in (4.16) and
in (4.16) and  in (4.17), we have
in (4.17), we have

Therefore, Theorem 4.1 holds and the proof is complete.
References
Agarwal RP, O'Regan D: Nonlinear superlinear singular and nonsingular second order boundary value problems. Journal of Differential Equations 1998, 143(1):60-95. 10.1006/jdeq.1997.3353
Liu L, Kang P, Wu Y, Wiwatanapataphee B: Positive solutions of singular boundary value problems for systems of nonlinear fourth order differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008, 68(3):485-498. 10.1016/j.na.2006.11.014
O'Regan D: Theory of Singular Boundary Value Problems. World Scientific, River Edge, NJ, USA; 1994:xii+154.
Zhang Y: Positive solutions of singular sublinear Emden-Fowler boundary value problems. Journal of Mathematical Analysis and Applications 1994, 185(1):215-222. 10.1006/jmaa.1994.1243
Wei Z:Existence of positive solutions for
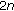 th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005, 306(2):619-636. 10.1016/j.jmaa.2004.10.037
th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005, 306(2):619-636. 10.1016/j.jmaa.2004.10.037Wei Z, Pang C:The method of lower and upper solutions for fourth order singular
 -point boundary value problems. Journal of Mathematical Analysis and Applications 2006, 322(2):675-692. 10.1016/j.jmaa.2005.09.064
-point boundary value problems. Journal of Mathematical Analysis and Applications 2006, 322(2):675-692. 10.1016/j.jmaa.2005.09.064Aftabizadeh AR: Existence and uniqueness theorems for fourth-order boundary value problems. Journal of Mathematical Analysis and Applications 1986, 116(2):415-426. 10.1016/S0022-247X(86)80006-3
Agarwal RP: On fourth order boundary value problems arising in beam analysis. Differential and Integral Equations 1989, 2(1):91-110.
Bai Z: The method of lower and upper solutions for a bending of an elastic beam equation. Journal of Mathematical Analysis and Applications 2000, 248(1):195-202. 10.1006/jmaa.2000.6887
Franco D, O'Regan D, Perán J: Fourth-order problems with nonlinear boundary conditions. Journal of Computational and Applied Mathematics 2005, 174(2):315-327. 10.1016/j.cam.2004.04.013
Gupta CP: Existence and uniqueness theorems for the bending of an elastic beam equation. Applicable Analysis 1988, 26(4):289-304. 10.1080/00036818808839715
Li Y: On the existence of positive solutions for the bending elastic beam equations. Applied Mathematics and Computation 2007, 189(1):821-827. 10.1016/j.amc.2006.11.144
Yao Q: Positive solutions of a nonlinear elastic beam equation rigidly fastened on the left and simply supported on the right. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(5-6):1570-1580. 10.1016/j.na.2007.07.002
Yao Q: Existence and multiplicity of positive solutions to a singular elastic beam equation rigidly fixed at both ends. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(8):2683-2694. 10.1016/j.na.2007.08.043
Yao Q: Monotonically iterative method of nonlinear cantilever beam equations. Applied Mathematics and Computation 2008, 205(1):432-437. 10.1016/j.amc.2008.08.044
Yao Q: Solvability of singular cantilever beam equation. Annals of Differential Equations 2008, 24(1):93-99.
Yao QL: Positive solution to a singular equation for a beam which is simply supported at left and clamped at right by sliding clamps. Journal of Yunnan University. Natural Sciences 2009, 31(2):109-113.
Yao QL: Existence and multiplicity of positive solutions to a class of nonlinear cantilever beam equations. Journal of Systems Science & Mathematical Sciences 2009, 29(1):63-69.
Yao QL: Positive solutions to a class of singular elastic beam equations rigidly fixed at both ends. Journal of Wuhan University. Natural Science Edition 2009, 55(2):129-133.
Yao Q: Existence of solution to a singular beam equation fixed at left and clamped at right by sliding clamps. Journal of Natural Science. Nanjing Normal University 2007, 9(1):1-5.
Graef JR, Kong L: A necessary and sufficient condition for existence of positive solutions of nonlinear boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(11):2389-2412. 10.1016/j.na.2006.03.028
Xu Y, Li L, Debnath L: A necessary and sufficient condition for the existence of positive solutions of singular boundary value problems. Applied Mathematics Letters 2005, 18(8):881-889. 10.1016/j.aml.2004.07.029
Zhao J, Ge W: A necessary and sufficient condition for the existence of positive solutions to a kind of singular three-point boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(9):3973-3980. 10.1016/j.na.2009.02.067
Zhao ZQ: Positive solutions of boundary value problems for nonlinear singular differential equations. Acta Mathematica Sinica 2000, 43(1):179-188.
Zhao Z:On the existence of positive solutions for
 -order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(11):2553-2561. 10.1016/j.na.2005.09.003
-order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(11):2553-2561. 10.1016/j.na.2005.09.003Ma R, An Y: Global structure of positive solutions for nonlocal boundary value problems involving integral conditions. Nonlinear Analysis: Theory, Methods & Applications 2009, 71(10):4364-4376. 10.1016/j.na.2009.02.113
Ma R, Xu J: Bifurcation from interval and positive solutions of a nonlinear fourth-order boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(1):113-122. 10.1016/j.na.2009.06.061
Ma RY, Thompson B: Nodal solutions for a nonlinear fourth-order eigenvalue problem. Acta Mathematica Sinica 2008, 24(1):27-34. 10.1007/s10114-007-1009-6
Dancer E: Global solutions branches for positive maps. Archive for Rational Mechanics and Analysis 1974, 55: 207-213. 10.1007/BF00281748
Rabinowitz PH: Some aspects of nonlinear eigenvalue problems. The Rocky Mountain Journal of Mathematics 1973, 3(2):161-202. 10.1216/RMJ-1973-3-2-161
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Sun JX: A theorem in point set topology. Journal of Systems Science & Mathematical Sciences 1987, 7(2):148-150.
Acknowledgments
This work is carried out while the author is visiting the University of New England. The author thanks Professor Yihong Du for his valuable advices and the Department of Mathematics for providing research facilities. The author also thanks the anonymous referees for their carefully reading of the first draft of the manuscript and making many valuable suggestions. Research is supported by the NSFC (10871120) and HESTPSP (J09LA08).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lu, H. Eigenvalue Problem and Unbounded Connected Branch of Positive Solutions to a Class of Singular Elastic Beam Equations. Bound Value Probl 2011, 594128 (2011). https://doi.org/10.1155/2011/594128
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/594128
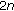 th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005, 306(2):619-636. 10.1016/j.jmaa.2004.10.037
th-order singular sublinear boundary value problems. Journal of Mathematical Analysis and Applications 2005, 306(2):619-636. 10.1016/j.jmaa.2004.10.037 -point boundary value problems. Journal of Mathematical Analysis and Applications 2006, 322(2):675-692. 10.1016/j.jmaa.2005.09.064
-point boundary value problems. Journal of Mathematical Analysis and Applications 2006, 322(2):675-692. 10.1016/j.jmaa.2005.09.064 -order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(11):2553-2561. 10.1016/j.na.2005.09.003
-order singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(11):2553-2561. 10.1016/j.na.2005.09.003