- Research Article
- Open access
- Published:
Three Solutions for Forced Duffing-Type Equations with Damping Term
Boundary Value Problems volume 2011, Article number: 736093 (2011)
Abstract
Using the variational principle of Ricceri and a local mountain pass lemma, we study the existence of three distinct solutions for the following resonant Duffing-type equations with damping and perturbed term  , a.e.
, a.e.  ,
,  and without perturbed term
and without perturbed term  , a.e.
, a.e.  ,
,  .
.
1. Introduction
In this paper, we consider the following resonant Duffing-type equations with damping and perturbed term:

where  ,
,  , and
, and  are continuous. Letting
are continuous. Letting  in problem (1.1) leads to
in problem (1.1) leads to

which is a common Duffing-type equation without perturbation.
The Duffing equation has been used to model the nonlinear dynamics of special types of mechanical and electrical systems. This differential equation has been named after the studies of Duffing in 1918 [1], has a cubic nonlinearity, and describes an oscillator. It is the simplest oscillator displaying catastrophic jumps of amplitude and phase when the frequency of the forcing term is taken as a gradually changing parameter. It has drawn extensive attention due to the richness of its chaotic behaviour with a variety of interesting bifurcations, torus and Arnolds tongues. The main applications have been in electronics, but it can also have applications in mechanics and in biology. For example, the brain is full of oscillators at micro and macro levels [2]. There are applications in neurology, ecology, secure communications, cryptography, chaotic synchronization, and so on. Due to the rich behaviour of these equations, recently there have been also several studies on the synchronization of two coupled Duffing equations [3, 4]. The most general forced form of the Duffing-type equation is

Recently, many authors have studied the existence of periodic solutions of the Duffing-type equation (1.3). By using various methods and techniques, such as polar coordinates, the method of upper and lower solutions and coincidence degree theory and a series of existence results of nontrivial solutions for the Duffing-type equations such as (1.3) have been obtained; we refer to [5–11] and references therein. There are also authors who studied the Duffing-type equations by using the critical point theory (see [12, 13]). In [12], by using a saddle point theorem, Tomiczek obtained the existence of a solution of the following Duffing-type system:

which is a special case of problems (1.1)-(1.2). However, to the best of our knowledge, there are few results for the existence of multiple solutions of (1.3).
Our aim in this paper is to study the variational structure of problems (1.1)-(1.2) in an appropriate space of functions and the existence of solutions for problems (1.1)-(1.2) by means of some critical point theorems. The organization of this paper is as follows. In Section 2, we shall study the variational structure of problems (1.1)-(1.2) and give some important lemmas which will be used in later section. In Section 3, by applying some critical point theorems, we establish sufficient conditions for the existence of three distinct solutions to problems (1.1)-(1.2).
2. Variational Structure
In the Sobolev space  , consider the inner product
, consider the inner product

inducing the norm

We also consider the inner product

and the norm

Obviously, the norm  and the norm
and the norm  are equivalent. So
are equivalent. So  is a Hilbert space with the norm
is a Hilbert space with the norm  .
.
By Poincaré's inequality,

where  ,
,  is the first eigenvalue of the problem
is the first eigenvalue of the problem

Usually, in order to find the solution of problems (1.1)-(1.2), we should consider the following functional  ,
,  defined on
defined on  :
:

where  ,
,  .
.
Finding solutions of problem (1.1) is equivalent to finding critical points of  in
in  and
and

Lemma 2.1 (Hölder Inequality).
Let f, g  ,
,  , and
, and  the conjugate number of
the conjugate number of  . Then
. Then

Lemma 2.2.
Assume the following condition holds.
(f1) There exist positive constants  ,
,  , and
, and  such that
such that

Then  is coercive.
is coercive.
Proof.
Let  be a sequence such that
be a sequence such that  . It follows from (f1) and Hölder inequality that
. It follows from (f1) and Hölder inequality that

which implies from  that
that  . This completes the proof.
. This completes the proof.
From the proof of Lemma 2.2, we can show the following Lemma.
Lemma 2.3.
Assume that  and the following condition holds.
and the following condition holds.
(f2)There exist positive constants  and
and  such that
such that

Then  is coercive.
is coercive.
Lemma 2.4.
Assume the following condition holds.
(f3) for all
for all  .
.
Then  is coercive.
is coercive.
Proof.
Let  be a sequence such that
be a sequence such that  . Fix
. Fix  , from (f3), there exists
, from (f3), there exists  such that
such that

Denote by  the set
the set  and by
and by  its complement in
its complement in  . Put
. Put  for all
for all  . By the continuity of
. By the continuity of  , we know that
, we know that  . Then one has
. Then one has

which implies that  . This completes the proof.
. This completes the proof.
Based on Ricceri's variational principle in [14, 15], Fan and Deng [16] obtained the following result which is a main tool used in our paper.
Lemma 2.5 (see [16]).
Suppose that  is a bounded convex open subset of
is a bounded convex open subset of  ,
,  ,
,  ,
,  ,
,  is a strict local minimizer of
is a strict local minimizer of  , and
, and  . Then, for
. Then, for  small enough and any
small enough and any  ,
,  , there exists
, there exists  such that for each
such that for each  ,
,  has at least two local minima
has at least two local minima  and
and  lying in
lying in  , where
, where  ,
,  , where
, where  , and
, and  .
.
3. Main Results
In this section, we will prove that problems (1.1)-(1.2) have three distinct solutions by using the variational principle of Ricceri and a local mountain pass lemma.
Theorem 3.1.
Assume that (f1) holds. Suppose further that
(f4) there exists  such that
such that

(f5) there exists  such that
such that  .
.
Then there exist  and
and  such that, for every
such that, for every  , problem (1.1) admits at least three distinct solutions which belong to
, problem (1.1) admits at least three distinct solutions which belong to  .
.
Proof.
By Lemma 2.2, condition (f1) implies that the functional  is coercive. Since
is coercive. Since  is sequentially weakly lower semicontinuous (see [16, Propositions 2.5 and 2.6]),
is sequentially weakly lower semicontinuous (see [16, Propositions 2.5 and 2.6]),  has a global minimizer
has a global minimizer  . By (f5), we obtain
. By (f5), we obtain  . Let
. Let  . Since
. Since  is coercive, we can choose a large enough
is coercive, we can choose a large enough  such that
such that

Now we prove that  has a strict local minimum at
has a strict local minimum at  . By the compact embedding of
. By the compact embedding of  into
into  , there exists a constant
, there exists a constant  such that
such that

Choosing  , it results that
, it results that

Therefore, for every  , it follows from (f4) that
, it follows from (f4) that

which implies that  is a strict local minimum of
is a strict local minimum of  in
in  with
with  .
.
At this point, we can apply Lemma 2.5 taking  and
and  as perturbing terms. Then, for
as perturbing terms. Then, for  small enough and any
small enough and any  ,
,  , we can obtain the following.
, we can obtain the following.
-
(i)
There exists
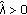 such that, for each
such that, for each  ,
, 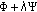 has two distinct local minima
has two distinct local minima  and
and 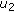 satisfying
satisfying

(ii) (see [16, Theorem 3.6])
(see [16, Theorem 3.6])
Let  be such that
be such that

and put  . Owing to the coerciveness of
. Owing to the coerciveness of  , there exists
, there exists  such that
such that  . Since
. Since  is continuous, then
is continuous, then

Choosing  , hence, for every
, hence, for every  with
with  , one has
, one has

and when 

Further, from (3.6), we have that  . Since
. Since  is arbitrary, letting
is arbitrary, letting  , we can obtain that
, we can obtain that

Therefore, by (3.6) and (3.11),  can be chosen small enough that
can be chosen small enough that

and (3.9)-(3.10) hold, for every  .
.
For a given  in the interval above, define the set of paths going from
in the interval above, define the set of paths going from  to
to 

and consider the real number  . Since
. Since  and each path
and each path  goes through
goes through  , one has
, one has  .
.
By (3.9) and (3.10), in the definition of  , there is no need to consider the paths going through
, there is no need to consider the paths going through  . Hence, there exists a sequence of paths
. Hence, there exists a sequence of paths  such that
such that  and
and

Applying a general mountain pass lemma without the (PS) condition (see [17, Theorem 2.8]), there exists a sequence  such that
such that  and
and  as
as  . Hence
. Hence  is a bounded
is a bounded  sequence and, taking into account the fact that
sequence and, taking into account the fact that  is an
is an  type mapping, admits a convergent subsequence to some
type mapping, admits a convergent subsequence to some  . So, such
. So, such  turns to be a critical point of
turns to be a critical point of  , with
, with  , hence different from
, hence different from  and
and  and
and  . This completes the proof.
. This completes the proof.
Taking  in Theorem 3.1, we can obtain the existence of three distinct solutions for the Duffing-type equation without perturbation (1.2) as following.
in Theorem 3.1, we can obtain the existence of three distinct solutions for the Duffing-type equation without perturbation (1.2) as following.
Theorem 3.2.
Assume that (f1), (f4), and (f5) hold; then problem (1.2) admits at least three distinct solutions.
Together with Lemma 2.3 and Lemma 2.4, we can easily show that the following corollary.
Corollary 3.3.
Assume that (f2), (f4), and (f5) hold; then there exist  and
and  such that, for every
such that, for every  , problem (1.1) admits at least three distinct solutions which belong to
, problem (1.1) admits at least three distinct solutions which belong to  . Furthermore, problem (1.2) admits at least three distinct solutions.
. Furthermore, problem (1.2) admits at least three distinct solutions.
Corollary 3.4.
Assume that (f3), (f4), and (f5); hold, then there exist  and
and  such that, for every
such that, for every  , problem (1.1) admits at least three distinct solutions which belong to
, problem (1.1) admits at least three distinct solutions which belong to  . Furthermore, problem (1.2) admits at least three distinct solutions.
. Furthermore, problem (1.2) admits at least three distinct solutions.
4. Some Examples
Example 4.1.
Consider the following resonant Duffing-type equations with damping and perturbed term

where  ,
,  ,
,  ,
,  , and
, and

in which  satisfy
satisfy

Then there exists  , for every
, for every  , problem (8) admits at least three distinct solutions.
, problem (8) admits at least three distinct solutions.
Proof.
Obviously, from the definitions of  and
and  , it is easy to see that
, it is easy to see that  is continuous and (f1) holds. Taking
is continuous and (f1) holds. Taking  , for
, for  , we have that
, we have that

which implies that (f4) is satisfied. Define

Clearly,  . Then we obtain that
. Then we obtain that

So  , which implies that (f5) is satisfied. To this end, all assumptions of Theorem 3.1 hold. By Theorem 3.1, there exists
, which implies that (f5) is satisfied. To this end, all assumptions of Theorem 3.1 hold. By Theorem 3.1, there exists  , for every
, for every  , problem (8) admits at least three distinct solutions.
, problem (8) admits at least three distinct solutions.
Example 4.2.
Let  . From Example 4.1, we can obtain that the following resonant Duffing-type equations with damping:
. From Example 4.1, we can obtain that the following resonant Duffing-type equations with damping:

admits at least three distinct solutions.
References
Duffing G: Erzwungene Schwingungen bei veränderlicher Eigenfrequenz und ihre Technische Beduetung. Vieweg Braunschweig, 1918
Zeeman EC: Duffing's equation in brain modelling. Bulletin of the Institute of Mathematics and Its Applications 1976, 12(7):207-214.
Njah AN, Vincent UE: Chaos synchronization between single and double wells Duffing-Van der Pol oscillators using active control. Chaos, Solitons and Fractals 2008, 37(5):1356-1361. 10.1016/j.chaos.2006.10.038
Wu X, Cai J, Wang M: Global chaos synchronization of the parametrically excited Duffing oscillators by linear state error feedback control. Chaos, Solitons and Fractals 2008, 36(1):121-128. 10.1016/j.chaos.2006.06.014
Peng L: Existence and uniqueness of periodic solutions for a kind of Duffing equation with two deviating arguments. Mathematical and Computer Modelling 2007, 45(3-4):378-386. 10.1016/j.mcm.2006.05.012
Chen H, Li Y: Rate of decay of stable periodic solutions of Duffing equations. Journal of Differential Equations 2007, 236(2):493-503. 10.1016/j.jde.2007.01.023
Lazer AC, McKenna PJ: On the existence of stable periodic solutions of differential equations of Duffing type. Proceedings of the American Mathematical Society 1990, 110(1):125-133. 10.1090/S0002-9939-1990-1013974-9
Du B, Bai C, Zhao X: Problems of periodic solutions for a type of Duffing equation with state-dependent delay. Journal of Computational and Applied Mathematics 2010, 233(11):2807-2813. 10.1016/j.cam.2009.11.026
Wang Y, Ge W:Periodic solutions for Duffing equations with a
 -Laplacian-like operator. Computers & Mathematics with Applications 2006, 52(6-7):1079-1088. 10.1016/j.camwa.2006.03.030
-Laplacian-like operator. Computers & Mathematics with Applications 2006, 52(6-7):1079-1088. 10.1016/j.camwa.2006.03.030Njoku FI, Omari P: Stability properties of periodic solutions of a Duffing equation in the presence of lower and upper solutions. Applied Mathematics and Computation 2003, 135(2-3):471-490. 10.1016/S0096-3003(02)00062-0
Wang Z, Xia J, Zheng D: Periodic solutions of Duffing equations with semi-quadratic potential and singularity. Journal of Mathematical Analysis and Applications 2006, 321(1):273-285. 10.1016/j.jmaa.2005.08.033
Tomiczek P: The Duffing equation with the potential Landesman-Lazer condition. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(2):735-740. 10.1016/j.na.2008.01.006
Li Y, Zhang T: On the existence of solutions for impulsive Duffing dynamic equations on time scales with Dirichlet boundary conditions. Abstract and Applied Analysis 2010, 2010:-27.
Ricceri B: A general variational principle and some of its applications. Journal of Computational and Applied Mathematics 2000, 113(1-2):401-410. 10.1016/S0377-0427(99)00269-1
Ricceri B: Sublevel sets and global minima of coercive functionals and local minima of their perturbations. Journal of Nonlinear and Convex Analysis 2004, 5(2):157-168.
Fan X, Deng S-G:Remarks on Ricceri's variational principle and applications to the
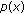 -Laplacian equations. Nonlinear Analysis. Theory, Methods & Applications 2007, 67(11):3064-3075. 10.1016/j.na.2006.09.060
-Laplacian equations. Nonlinear Analysis. Theory, Methods & Applications 2007, 67(11):3064-3075. 10.1016/j.na.2006.09.060Willem M: Minimax Theorems. Birkhäuser, Boston, Mass, USA; 1996:x+162.
Acknowledgment
This work is supported by the National Natural Sciences Foundation of People's Republic of China under Grant no. 10971183.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Y., Zhang, T. Three Solutions for Forced Duffing-Type Equations with Damping Term. Bound Value Probl 2011, 736093 (2011). https://doi.org/10.1155/2011/736093
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/736093
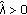 such that, for each
such that, for each  ,
, 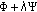 has two distinct local minima
has two distinct local minima  and
and 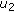 satisfying
satisfying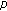 -Laplacian-like operator. Computers & Mathematics with Applications 2006, 52(6-7):1079-1088. 10.1016/j.camwa.2006.03.030
-Laplacian-like operator. Computers & Mathematics with Applications 2006, 52(6-7):1079-1088. 10.1016/j.camwa.2006.03.030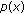 -Laplacian equations. Nonlinear Analysis. Theory, Methods & Applications 2007, 67(11):3064-3075. 10.1016/j.na.2006.09.060
-Laplacian equations. Nonlinear Analysis. Theory, Methods & Applications 2007, 67(11):3064-3075. 10.1016/j.na.2006.09.060