- Research Article
- Open access
- Published:
Second-order estimates for boundary blowup solutions of special elliptic equations
Boundary Value Problems volume 2006, Article number: 45859 (2006)
Abstract
We find a second-order approximation of the boundary blowup solution of the equation , with
, with , in a bounded smooth domain
, in a bounded smooth domain . Furthermore, we consider the equation
. Furthermore, we consider the equation . In both cases, we underline the effect of the geometry of the domain in the asymptotic expansion of the solutions near the boundary
. In both cases, we underline the effect of the geometry of the domain in the asymptotic expansion of the solutions near the boundary .
.
References
Andersson L, Chruściel PT: Solutions of the constraint equations in general relativity satisfying "hyperboloidal boundary conditions". Dissertationes Mathematicae (Rozprawy Matematyczne) 1996, 355: 1-100.
Anedda C, Buttu A, Porru G: Boundary estimates for blow-up solutions of elliptic equations with exponential growth. to appear in Proceedings Differential and Difference Equations
Anedda C, Porru G: Higher order boundary estimates for blow-up solutions of elliptic equations. to appear in Differential Integral Equations
Bandle C: Asymptotic behaviour of large solutions of quasilinear elliptic problems. Zeitschrift für Angewandte Mathematik und Physik 2003,54(5):731-738. 10.1007/s00033-003-3207-0
Bandle C, Giarrusso E: Boundary blow up for semilinear elliptic equations with nonlinear gradient terms. Advances in Differential Equations 1996,1(1):133-150.
Bandle C, Marcus M: "Large" solutions of semilinear elliptic equations: existence, uniqueness and asymptotic behaviour. Journal d'Analyse Mathématique 1992, 58: 9-24.
Bandle C, Marcus M: On second-order effects in the boundary behaviour of large solutions of semilinear elliptic problems. Differential and Integral Equations 1998,11(1):23-34.
Bandle C, Marcus M: Dependence of blowup rate of large solutions of semilinear elliptic equations, on the curvature of the boundary. Complex Variables. Theory and Application 2004,49(7–9):555-570.
Berhanu S, Porru G: Qualitative and quantitative estimates for large solutions to semilinear equations. Communications in Applied Analysis 2000,4(1):121-131.
Bieberbach L:
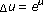 und die automorphen Funktionen. Mathematische Annalen 1916,77(2):173-212. 10.1007/BF01456901
und die automorphen Funktionen. Mathematische Annalen 1916,77(2):173-212. 10.1007/BF01456901del Pino M, Letelier R: The influence of domain geometry in boundary blow-up elliptic problems. Nonlinear Analysis. Theory, Methods & Applications. Series A: Theory and Methods 2002,48(6):897-904.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Grundlehren der mathematischen Wissenschaften. Volume 224. Springer, Berlin; 1977:x+401.
Greco A, Porru G: Asymptotic estimates and convexity of large solutions to semilinear elliptic equations. Differential and Integral Equations 1997,10(2):219-229.
Keller JB:On solutions of
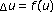 . Communications on Pure and Applied Mathematics 1957, 10: 503-510. 10.1002/cpa.3160100402
. Communications on Pure and Applied Mathematics 1957, 10: 503-510. 10.1002/cpa.3160100402Lazer AC, McKenna PJ: Asymptotic behavior of solutions of boundary blowup problems. Differential and Integral Equations 1994,7(3-4):1001-1019.
Osserman R:On the inequality
 . Pacific Journal of Mathematics 1957,7(4):1641-1647.
. Pacific Journal of Mathematics 1957,7(4):1641-1647.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Anedda, C., Buttu, A. & Porru, G. Second-order estimates for boundary blowup solutions of special elliptic equations. Bound Value Probl 2006, 45859 (2006). https://doi.org/10.1155/BVP/2006/45859
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/45859
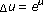 und die automorphen Funktionen. Mathematische Annalen 1916,77(2):173-212. 10.1007/BF01456901
und die automorphen Funktionen. Mathematische Annalen 1916,77(2):173-212. 10.1007/BF01456901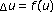 . Communications on Pure and Applied Mathematics 1957, 10: 503-510. 10.1002/cpa.3160100402
. Communications on Pure and Applied Mathematics 1957, 10: 503-510. 10.1002/cpa.3160100402 . Pacific Journal of Mathematics 1957,7(4):1641-1647.
. Pacific Journal of Mathematics 1957,7(4):1641-1647.