- Research Article
- Open access
- Published:
Two-point boundary value problems for higher-order linear differential equations with strong singularities
Boundary Value Problems volume 2006, Article number: 83910 (2006)
Abstract
For strongly singular higher-order linear differential equations together with two-point conjugate and right-focal boundary conditions, we provide easily verifiable best possible conditions which guarantee the existence of a unique solution.
References
Agarwal RP: Focal boundary value problems for differential and difference equations, Mathematics and Its Applications. Volume 436. Kluwer Academic Publishers, Dordrecht; 1998:x+289.
Agarwal RP, O'Regan D: Singular differential and integral equations with applications. Kluwer Academic Publishers, Dordrecht; 2003:xii+402.
Kiguradze IT: On a singular boundary value problem. Journal of Mathematical Analysis and Applications. 1970,30(3):475–489. 10.1016/0022-247X(70)90135-6
Kiguradze IT: On a singular multi-point boundary value problem. Annali di Matematica Pura ed Applicata. Series IV. 1970, 86: 367–399. 10.1007/BF02415727
Kiguradze I: Some singular boundary value problems for ordinary differential equations. Tbilisi University Press, Tbilisi; 1975.
Kiguradze I: Some optimal conditions for the solvability of two-point singular boundary value problems. Functional Differential Equations 2003,10(1–2):259–281. Functional differential equations and applications (Beer-Sheva, 2002)
Kiguradze I: On two-point boundary value problems for higher order singular ordinary differential equations. Georgian Academy of Sciences. A. Razmadze Mathematical Institute. Memoirs on Differential Equations and Mathematical Physics 2004, 31: 101–107.
Kiguradze IT, Chanturia TA: Asymptotic properties of solutions of nonautonomous ordinary differential equations, Mathematics and Its Applications (Soviet Series). Volume 89. Kluwer Academic Publishers, Dordrecht; 1993:xiv+331. Translated from the 1985 Russian original
Kiguradze I, Půža B: Conti-Opial type existence and uniqueness theorems for nonlinear singular boundary value problems. Functional Differential Equations 2002,9(3–4):405–422. Dedicated to L. F. Rakhmatullina and N. V. Azbelev on the occasion of their seventieth and eightieth birthdays
Kiguradze I, Půža B, Stavroulakis IP: On singular boundary value problems for functional differential equations of higher order. Georgian Mathematical Journal 2001,8(4):791–814.
Kiguradze IT, Shekhter BL: Singular boundary value problems for second-order ordinary differential equations. In Current problems in mathematics. Newest results, Vol. 30 (Russian), Itogi Nauki i Tekhniki. Akad. Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow; 1987:105–201, 204. Translated in J. Soviet Math. 43 (1988), no. 2, 2340–2417
Kiguradze I, Tskhovrebadze G: On two-point boundary value problems for systems of higher-order ordinary differential equations with singularities. Georgian Mathematical Journal 1994,1(1):31–45. 10.1007/BF02315301
Maĭorov VE: On the existence of solutions of higher-order singular differential equations. Rossiĭskaya Akademiya Nauk. Matematicheskie Zametki 1992,51(3):75–84. translation in Math. Notes 51 (1992), no. 3–4, 274–281
Půža B: On a singular two-point boundary value problem for the nonlinearth-order differential equation with deviating arguments. Georgian Mathematical Journal 1997,4(6):557–566. 10.1023/A:1022107625905
Půža B, Rabbimov A: On a weighted boundary value problem for a system of singular functional-differential equations. Georgian Academy of Sciences. A. Razmadze Mathematical Institute. Memoirs on Differential Equations and Mathematical Physics 2000, 21: 125–130.
Tskhovrebadze GD: On a multipoint boundary value problem for linear ordinary differential equations with singularities. Universitatis Masarykianae Brunensis. Facultas Scientiarum Naturalium. Archivum Mathematicum 1994,30(3):171–206.
Tskhovrebadze G: On the modified boundary value problem of de la Vallée–Poussin for nonlinear ordinary differential equations. Georgian Mathematical Journal 1994,1(4):429–458. 10.1007/BF02307450
Wong PJY, Agarwal RP: Singular differential equations with
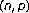 boundary conditions. Mathematical and Computer Modelling 1998,28(1):37–44. 10.1016/S0895-7177(98)00079-X
boundary conditions. Mathematical and Computer Modelling 1998,28(1):37–44. 10.1016/S0895-7177(98)00079-X
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R., Kiguradze, I. Two-point boundary value problems for higher-order linear differential equations with strong singularities. Bound Value Probl 2006, 83910 (2006). https://doi.org/10.1155/BVP/2006/83910
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/83910
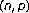 boundary conditions. Mathematical and Computer Modelling 1998,28(1):37–44. 10.1016/S0895-7177(98)00079-X
boundary conditions. Mathematical and Computer Modelling 1998,28(1):37–44. 10.1016/S0895-7177(98)00079-X