Pullback attractors for three-dimensional Navier-Stokes-Voigt equations with delays

Abstract

Our aim in this paper is to study the existence of pullback attractors for the 3D Navier-Stokes-Voigt equations with delays. The forcing term $g(t,u(t-\rho (t)))$ containing the delay is sub-linear and continuous with respect to u. Since the solution of the model is not unique, which is caused by the continuity assumption, we establish the existence of pullback attractors for our problem by using the theory of multi-valued dynamical system.

1 Introduction

Let $\mathrm{\Omega }\subset {\mathbb{R}}^3$ be an open, bounded and connected set. We consider the following problem for three-dimensional Navier-Stokes-Voigt (NSV) equations with delays in continuous and sub-linear operators:

$$\{\begin{array}{ll}{u}_t-\nu \mathrm{△}u-{\alpha }^2\mathrm{△}{u}_t+(u\cdot \mathrm{\nabla })u+\mathrm{\nabla }p=g(t,u(t-\rho (t))),& \text{in }(\tau ,+\mathrm{\infty })\times \mathrm{\Omega },\\ divu=0,& \text{in }(\tau ,+\mathrm{\infty })\times \mathrm{\Omega },\\ u(x,t)=0,& \text{on }(\tau ,+\mathrm{\infty })\times \partial \mathrm{\Omega },\\ u(\tau ,x)=u_0(x),& x\in \mathrm{\Omega },\\ u(\tau +t,x)=\phi (t,x),& t\in (-h,0),x\in \mathrm{\Omega }.\end{array}$$

(1.1)

Here $u=(u_1(t,x),u_2(t,x),u_3(t,x))$ is the velocity vector field, ν is a positive constant, α is a characterizing parameter of the elasticity of the fluid, p is the pressure, g is the external force term which contains memory effects during a fixed interval of time of length $h>0$, $\rho (t)$ is an adequate given delay function, $u_0$ is the initial velocity field at the initial time $\tau \in \mathbb{R}$, φ is the initial datum on the interval $(-h,0)$.

Equation (1.1) with $\alpha =0$ becomes the classical three-dimensional Navier-Stokes (NS) equation. In the past decades, many authors [1–6] investigated intensively the classical three-dimensional incompressible NS equation. For the sake of direct numerical simulations for NS equations, the NSV model of viscoelastic incompressible fluid has been proposed as a regularization of NS equations.

Equation (1.1) governs the motion of a Klein-Voigt viscoelastic incompressible fluid. Oskolkov [7] was the first to introduce the system which gives an approximate description of the Kelvin-Voigt fluid (see, e.g., [8, 9]). In 2010, Levant et al. [10] investigated numerically the statistical properties of the Navier-Stokes-Voigt model. Kalantarov and Titi [11] studied a global attractor of a semigroup generated by equation (1.1) for the autonomous case. Recently, Luengo et al. [12] obtained asymptotic compactness by using the energy method, and they further got the existence of pullback attractors for three-dimensional non-autonomous NSV equations.

Let us recall some related results in the literature. Yue and Zhong [13] studied the long time behavior of the three-dimensional NSV model of viscoelastic incompressible fluid for system (1.1) by using a useful decomposition method. The authors in [12, 14] deduced the existence of 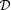-pullback attractors for 3D non-autonomous NSV equations using the energy method. As we know from [15], delay terms appear naturally. In recent years, Caraballo and Real [16–18] developed a fruitful theory of existence, uniqueness, stability of solutions and global attractors for Navier-Stokes models including some hereditary characteristics such as constant, variable delay, distributed delay, etc. However, our present problem has no uniqueness of solutions. To overcome the difficulty, we may cite the results by Ball [19] and by Marín-Rubio and Real [20]. Gal and Medjo [21] proved the existence of uniform global attractors for a Navier-Stokes-Voigt model with memory. As commented before, in comparison with three-dimensional Navier-Stokes equations, there is no regularizing effect. Our result of this paper is to establish the existence of pullback attractors for three-dimensional NSV equations in $H_0^1$ when the external forcing term $g(t,u)\in H$ and the function $g(t,u)$ is continuous with respect to u. Another difficulty is to obtain that the multi-valued processes are asymptotically compact. In 2007, Kapustyan and Valero [22] presented a method suitable for verifying the asymptotic compactness. The authors [20] applied this method to 2D Navier-Stokes equations with delays in continuous and sub-linear operators. We shall apply the energy method to prove that our multi-valued processes are asymptotically compact by making some minor modifications caused by the term $-{\alpha }^2\mathrm{\Delta }{u}_t$ in (1.1).

This paper is organized as follows. In Section 2, we recall briefly some results on the abstract theory of pullback attractors. In Section 3, we introduce some abstract spaces necessary for the variational statement of the problem and give the proof of the global existence of solutions. In Section 4, we consider the asymptotic behavior of problem (1.1).

2 Basic theory of pullback attractors

By using the framework of evolution processes, thanks to [20, 23, 24], we now briefly recall some theories of pullback attractors and the related results. On the one hand, we have to overcome some difficulties caused by multi-valued processes. On the other hand, since our model is non-autonomous, we should use the related results for classical multi-valued processes in [23, 24], but which are not completely adapted to our model.

Let $(X,d)$ be a metric space, and let $\mathcal{P}(X)$ be the class of nonempty subsets of X. As usual, we denote by ${dist}_X(B_1,B_2)$ the Hausdorff semi-distance in X between $B_1\subset X$ and $B_2\subset X$, i.e.,

$${dist}_X(B_1,B_2)=\underset{x\in B_1}{sup}\underset{y\in B_2}{inf}{d}_X(x,y)\text{for }{B}_1,B_2\subset X,$$

where $d_X(x,y)$ denotes the distance between two points x and y in X.

We now formulate an abstract result in order to establish the existence of pullback attractors for the multi-valued dynamical system associated with (1.1).

Definition 2.1 A multi-valued process U is a family of mappings $U(t,\tau ):X\to \mathcal{P}(X)$ for any pair $\tau \le t$ of real numbers such that

$$U(t,\tau )x\subset U(t,r)U(r,\tau )x,\mathrm{\forall }x\in X,\mathrm{\forall }\tau \le r\le t.$$

If the above relation is not only an inclusion but also an equality, we say that the multi-valued process is strict. For example, the relation generalized by 3D non-autonomous NSV equation (see, e.g., [12]) is an equality, while the relation generalized by 3D NS equations (see, e.g., [22]) is strict.

Definition 2.2 Suppose that ${\hat{D}}_0={\{D_0(t)\}}_{t\in \mathbb{R}}\subset \mathcal{P}(X)$ is a family of sets. A multi-valued process U is said to be ${\hat{D}}_0$-asymptotically compact if for any $t\in \mathbb{R}$, any sequences ${\{{\tau }_n\}}_{n=1}^{\mathrm{\infty }}$ with ${\tau }_n\to -\mathrm{\infty }$, $x_n\in D_0({\tau }_n)$, and ${\xi }_n\in U(t,{\tau }_n)x_n$, the sequence $\{{\xi }_n\}$ is relatively compact in X.

Lemma 2.1 If a multi-valued process U is ${\hat{D}}_0$-asymptotically compact, then the sets $\mathrm{\Lambda }({\hat{D}}_0,t)$ are nonempty compact subsets of X, where

$$\mathrm{\Lambda }({\hat{D}}_0,t)=\bigcap _{s\le t}{\overline{\bigcup _{\tau \le s}U(t,\tau )D_0(\tau )}}^X,\mathrm{\forall }t\in \mathbb{R}.$$

Furthermore, $\mathrm{\Lambda }({\hat{D}}_0,t)$ attracts in a pullback sense to ${\hat{D}}_0$ at time t, i.e.,

$$\underset{\tau \to -\mathrm{\infty }}{lim}dist(U(t,\tau )D_0(\tau ),\mathrm{\Lambda }({\hat{D}}_0,t))=0.$$

Indeed, it is the minimal closed set with this property.

Definition 2.3 The family of subsets ${\hat{D}}_0={\{D_0(t)\}}_{t\in \mathbb{R}}$ is said to be pullback-absorbing with respect to a multi-valued process U if for every $t\in \mathbb{R}$ and all bounded subset B of X, there exists a time $\tau (t,B)\le t$ such that

$$U(t,\tau )B\subset D_0(t),\mathrm{\forall }\tau \le \tau (t,B).$$

Lemma 2.2 Let the family of sets ${\hat{D}}_0={\{D_0(t)\}}_{t\in \mathbb{R}}$ be pullback-absorbing for the multi-valued process U, and let U be ${\hat{D}}_0$-asymptotically compact. Then, for any bounded sets B of X, it holds that

$$\underset{\tau \to -\mathrm{\infty }}{lim}dist(U(t,\tau )B,\mathrm{\Lambda }({\hat{D}}_0,t))=0.$$

Definition 2.4 Suppose that U is a multi-valued process. A family $\mathcal{A}={\{\mathcal{A}(t)\}}_{t\in \mathbb{R}}\subset \mathcal{P}(X)$ is said to be a pullback attractor for a multi-valued process U if the set $\mathcal{A}(t)$ is compact for any $t\in \mathbb{R}$ and attracts at time t to any bounded set $B\subset X$ in a pullback sense, i.e.,

$$\underset{\tau \to -\mathrm{\infty }}{lim}dist(U(t,\tau )B,\mathcal{A}(t))=0.$$

We can see obviously that a pullback attractor does not need to be unique. However, it can be considered unique in the sense of minimal, that is, the minimal closed family with such a property. In this sense, we obtain the following property and the existence of pullback attractors.

Lemma 2.3 [25]

Assume that U is a multi-valued process, and U is ${\hat{D}}_0$-asymptotically compact and a family ${\hat{D}}_0$ is pullback-absorbing for U. Then, for any $t\in \mathbb{R}$ and any bounded subset B of X, the set

$$\mathrm{\Lambda }(B,t)=\bigcap _{s\le t}{\overline{\bigcup _{\tau \le s}U(t,\tau )B}}^X,\mathrm{\forall }t\in \mathbb{R},$$

is a nonempty compact subset contained in $\mathrm{\Lambda }({\hat{D}}_0,t)$, which attracts to B in a pullback sense. In fact, $\mathrm{\Lambda }({\hat{D}}_0,t)$ defined above is the minimal closed set with this property.

Furthermore, for any bounded set B, the set $\mathcal{A}(t)={\overline{{\bigcup }_B\mathrm{\Lambda }(B,t)}}^X$ is a pullback attractor. From Definitions 2.3 and 2.4, it is easy to see that $\mathcal{A}(t)\subset \mathrm{\Lambda }({\hat{D}}_0,t)$.

If there exists a time $T\in \mathbb{R}$ such that ${\bigcup }_{t\le T}{D}_0(t)$ is bounded, for bounded B, then

$$\mathcal{A}(t)={\overline{\bigcup _B\mathrm{\Lambda }(B,t)}}^X=\mathrm{\Lambda }({\hat{D}}_0,t),\mathrm{\forall }t\le T.$$

As we know, for the single-valued processes, the continuity of processes provides invariance; while in the multi-valued processes, the upper semi-continuity (defined below) provides negatively invariance of the omega limit sets $\mathrm{\Lambda }(B,t)$ and the attractor. The following is the definition of the upper semi-continuity of the multi-valued processes (see in [22]).

Definition 2.5 Let U be a multi-valued process on X. It is said to be upper semi-continuous if for all $t\ge \tau$, the mapping $U(t,\tau )$ is upper semi-continuous from X into , that is to say, given a converging sequence $x_n\to x$, for some sequence $\{y_n\}$ such that $y_n\in U(t,\tau )x_n$ for all n, there exists a subsequence of $\{y_n\}$ converging in X to an element of $U(t,\tau )x$.

Lemma 2.4 [22]

Assume that a multi-valued process U and a family ${\hat{D}}_0$. If, in addition, $U(t,\tau )$ is ${\hat{D}}_0$-asymptotically compact and upper semi-continuous, then the family ${\{\mathrm{\Lambda }({\hat{D}}_0,t)\}}_{t\in \mathbb{R}}$ is negatively invariant, i.e.,

$$\mathrm{\Lambda }({\hat{D}}_0,t)\subset U(t,\tau )\mathrm{\Lambda }({\hat{D}}_0,\tau ),\mathrm{\forall }t\ge \tau ,$$

where B is a bounded set B of X. The family ${\{\mathrm{\Lambda }(B,t)\}}_{t\in \mathbb{R}}$ is also negatively invariant and the family $\mathcal{A}(t)$ defined in Lemma  2.3 is also negatively invariant.

Lemma 2.5 [22]

Given a universe 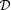, if a multi-valued process U is -asymptotically compact, then, for any $t\in \mathbb{R}$ and for any $\hat{D}\in D$, the omega limit set $\mathrm{\Lambda }(\hat{D},t)$ is a nonempty compact set of X that attracts to $\hat{D}$ at time t in a pullback sense. Indeed, it is the minimal closed set with this property. If, in addition, the multi-valued process U is upper semi-continuous, then ${\{\mathrm{\Lambda }(\hat{D},t)\}}_{t\in \mathbb{R}}$ is negatively invariant.

From the above lemmas, we obtain the following results which are rather similar to Theorem 3 in [20]. We only sketch it here.

Lemma 2.6 Suppose that is a universe and ${\hat{D}}_0$ is pullback -absorbing for a multi-valued process U, which is also ${\hat{D}}_0$-asymptotically compact. Then the results in Lemma  2.5 hold. Furthermore, the family ${\mathcal{A}}_{\mathcal{D}}={\{{\mathcal{A}}_{\mathcal{D}}(t)\}}_{t\in \mathbb{R}}$, where ${\mathcal{A}}_{\mathcal{D}}(t)=\mathrm{\Lambda }({\hat{D}}_0,t)$, and the following results hold:

• (1) For each $t\in \mathbb{R}$, the set ${\mathcal{A}}_{\mathcal{D}}(t)$ defined above is compact.

• (2) ${\mathcal{A}}_{\mathcal{D}}$ attracts pullback to any $\hat{D}\in \mathcal{D}$.

• (3) Suppose U is upper semi-continuous, then ${\mathcal{A}}_{\mathcal{D}}$ is negatively invariant.

• (4) ${\mathcal{A}}_{\mathcal{D}}(t)=\mathrm{\Lambda }({\hat{D}}_0,t)=\overline{{\bigcup }_{\hat{D}\in \mathcal{D}}\mathrm{\Lambda }(\hat{D},t)}$.

• (5) Assume ${\hat{D}}_0\in \mathcal{D}$, the minimal family of closed sets ${\mathcal{A}}_{\mathcal{D}}$ attracts pullback to elements of .

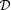• (6) Assume ${\hat{D}}_0\in \mathcal{D}$, each $D_0(t)$ is closed and the universe 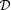is inclusion-closed, then ${\mathcal{A}}_{\mathcal{D}}\in \mathcal{D}$ and it is the only family of which satisfies the above properties (1), (2) and (3).

• (7) If contains the families of fixed bounded sets, then $\mathcal{A}={\{\mathcal{A}(t)\}}_{t\in \mathbb{R}}$ defined in Lemma  2.3 is the minimal pullback attractor of bounded sets, and $\mathcal{A}(t)\subset {\mathcal{A}}_{\mathcal{D}(t)}$ for each $t\in \mathbb{R}$. In addition, if there exists some $T\in \mathbb{R}$ such that ${\bigcup }_{t\le T}{D}_0(t)$ is bounded, then $\mathcal{A}(t)={\mathcal{A}}_{\mathcal{D}}(t)$ for all $t\le T$.

3 Introduction to some abstract spaces and the existence of solutions

We first recall some notations about the function spaces which will be used later to discuss the regularity of pullback attracting sets. Let us consider the following abstract space:

$$\mathcal{V}=\{u\in {(C_0^{\mathrm{\infty }}(\mathrm{\Omega }))}^3:divu=0\}.$$

The symbols H, V denote the closures of in $L^2{(\mathrm{\Omega })}^3$, $H_0^1{(\mathrm{\Omega })}^3$, respectively. In other words, H= the closure of in ${(L^2(\mathrm{\Omega }))}^3$ with the norm $|\cdot |$ and the inner product $(\cdot ,\cdot )$, where for $u,v\in {(L^2(\mathrm{\Omega }))}^3$,

$$(u,v)=\sum _{i=1}^2{\int }_{\mathrm{\Omega }}{u}_i(x)v_i(x)dx.$$

V= the closure of in ${(H_0^1(\mathrm{\Omega }))}^3$ with the norm associated to the inner product $((\cdot ,\cdot ))$, where for $u,v\in {(H_0^1(\mathrm{\Omega }))}^3$,

$$((u,v))=\sum _{i,j=1}^2{\int }_{\mathrm{\Omega }}\frac{\partial u_j}{\partial x_i}\frac{v_j}{\partial x_i}dx.$$

We shall use ${\parallel v\parallel }_{V^{\prime }}$ to denote the norm of $V^{\prime }$. The value of a functional from $V^{\prime }$ on an element from V is denoted by brackets $〈\cdot ,\cdot 〉$. It follows that $V\subset H\equiv H\subset V^{\prime }$, and the injections are dense and compact.

Define $\mathit{Au}=-P\mathrm{△}u$ for all $u\in D(A)$, where P is the ortho-projector from ${(L^2(\mathrm{\Omega }))}^3$ onto H. Considering the properties of the operator A, we have $A:V\to V^{\prime }$ as

$$〈\mathit{Au},v〉:=((u,v)),\mathrm{\forall }u,v\in V.$$

We define

$$b(u,v,w)=\sum _{i,j=1}^3{\int }_{\mathrm{\Omega }}{u}_i\frac{\partial v_j}{\partial x_i}{w}_{j}dx,$$

for every function u, v, $w:\mathrm{\Omega }\to {\mathbb{R}}^3$, and the operator $B:V\times V\to V^{\prime }$ as

$$〈B(u,v),w〉=b(u,v,w),\mathrm{\forall }u,v,w\in V.$$

Obviously, $b(u,v,w)$ is a continuous trilinear form such that

$$|b(u,v,w)|\le C_1\parallel u\parallel \parallel v\parallel \parallel w\parallel ,\mathrm{\forall }u,v,w\in V,$$

which yields

$${\parallel B(u,v)\parallel }_{V^{\prime }}\le C_1\parallel u\parallel \parallel v\parallel ,\mathrm{\forall }u,v\in V.$$

Moreover, b and B satisfy the following:

$$\begin{array}{c}b(u,v,w)=-b(u,w,v),\mathrm{\forall }u,v,w\in V,\hfill \\ b(u,v,v)=0,\mathrm{\forall }u,v,w\in V.\hfill \end{array}$$

Now, we make some assumptions. The given delay function ρ satisfies $\rho \in C^1([0,+\mathrm{\infty });[0,h])$, and there is a constant ${\rho }_0$ independent of t satisfying

$${\rho }^{\prime }(t)\le {\rho }_0<1\mathrm{\forall }t\ge 0,$$

(3.1)

where ${\rho }^{\prime }=\frac{d\rho }{dt}$.

Moreover, we assume that $g:[\tau ,+\mathrm{\infty })\times H\to H$ satisfies the following assumptions:

(H1) $g(\cdot ,u):[\tau ,+\mathrm{\infty })\to H$ is measurable for all $u\in V$.

(H2) For all $t\ge \tau$, $g(t,\cdot ):H\to H$ is continuous.

(H3) There exist two functions $\gamma ,\beta :[\tau ,+\mathrm{\infty })\to [0,+\mathrm{\infty })$. The above $\gamma \in L^p(\tau ,T)$ and $\beta \in L^1(\tau ,T)$ for all $T>\tau$, for $1\le p\le +\mathrm{\infty }$, such that ${\parallel g(t,u)\parallel }_{V^{\prime }}^2\le \gamma (t){\parallel u\parallel }^2+\beta (t)$, $\mathrm{\forall }t\ge \tau$, $\mathrm{\forall }u\in V$.

As to the initial datum, we assume

(H4) $u_0\in V$, and $\phi \in L^{2q}(-h,0;V)$, where $\frac{1}{p}+\frac{1}{q}=1$.

Next, we shall consider the solution of (1.1).

$$\{\begin{array}{l}u(t)+{\alpha }^2\mathit{Au}(t)+{\int }_{\tau }^t(\nu \mathit{Au}(s)+B(u(s)))ds\\ =u_0+{\alpha }^2{\mathit{Au}}_0+{\int }_{\tau }^{t}g(s,u(s-\rho (s)))ds,\mathrm{\forall }t\ge \tau ,\\ u(\tau +t)=\phi (t),\text{a.e. }t\in (-h,0).\end{array}$$

(3.2)

Definition 3.1 It is said that u is a weak solution to (1.1) if u belongs to $u\in L^{2q}(\tau -h,T;V)\cap L^{\mathrm{\infty }}(\tau ,T;V)$ for all $t\ge \tau$ such that $u(\tau +t)$ coincides with $\phi (t)$ in $(-h,0)$ and satisfies equation (3.2) in $V^{\prime }$ for all $t\ge \tau$.

If u is a solution of (3.2), then it is easy to get $u(t)+{\alpha }^2\mathit{Au}(t)\in L^2(\tau ,T;V^{\prime })$, and $\frac{d}{dt}(u(t)+{\alpha }^2\mathit{Au}(t))\in L^1(\tau ,T;V^{\prime })$ for all $T>\tau$. From the property of the operator A, we have $u(t)+{\alpha }^2\mathit{Au}(t)\in C(\tau ,+\mathrm{\infty };V^{\prime })$. On the other hand, reasoning as in [12], we have $u\in C([\tau ,+\mathrm{\infty });V)$.

Now, we define a functional $\tilde{\gamma }(t)=\gamma \circ {\zeta }^{-1}(t)$, where $\zeta :[\tau ,+\mathrm{\infty })\to [\rho (\tau ),+\mathrm{\infty })$ is a differentiable and nonnegative strictly increasing function given by $\zeta (s)=s-\rho (s)$. We have

$$\begin{array}{r}{\int }_{\tau }^t{\parallel g(t,u(t-\rho (t)))\parallel }_{V^{\prime }}^{2}dt\\ \le {\int }_{\tau }^T\gamma (t){\parallel u(t-\rho (t))\parallel }^{2}dt+{\int }_{\tau }^T\beta (t)dt\\ \le \frac{1}{1-{\rho }_0}{\int }_{\tau -\rho (\tau )}^{T-\rho (T)}\tilde{\gamma }(t){\parallel u(t)\parallel }^{2}dt+{\int }_{\tau }^T\beta (t)dt\\ \le \frac{1}{1-{\rho }_0}({\int }_{-\rho (\tau )}^0\tilde{\gamma }(t+\tau ){\parallel \phi \parallel }^{2}dt+{\int }_{\tau }^T\tilde{\gamma }(t){\parallel u(t)\parallel }^{2}dt)+{\int }_{\tau }^T\beta (t)dt.\end{array}$$

(3.3)

From the above analysis, taking into account $\tilde{\gamma }(t)\in L^P(-\rho (\tau ),T)$ for all $T>\tau$, we obtain that $g(t,u(t-\rho (t)))\in L^2(\tau ,T;V^{\prime })$. Hence, it is clear that u is a weak solution to (1.1) if $u\in C([\tau ,+\mathrm{\infty });V)$, $u^{\prime }\in L^2(\tau ,T;V)$ for all $T>\tau$, and satisfies the energy equality

$$\frac{1}{2}\frac{d}{dt}({|u(t)|}^2+{\alpha }^2{\parallel u(t)\parallel }^2)+\nu {\parallel u(t)\parallel }^2=〈g(t,u(t-\rho (t))),u(t)〉,\text{a.e. }t>\tau$$

in the distributional sense on $(\tau ,+\mathrm{\infty })$.

Theorem 3.1 Suppose that (H1)-(H4) hold. Then there exists a global solution u to (3.2).

Proof We shall prove the result by the Faedo-Galerkin scheme and compactness method. For convenience and without loss of generality, we set the initial time $\tau =0$. As to different value τ, we only proceed by translation.

Consider the Hilbert basis of H formed by the eigenfunctions $\{v_k\}$ of the above operator A, i.e., $A{v}_k={\lambda }_k{v}_k$. In fact, these elements allow to define the operator $P_{m}v={\sum }_{k=1}^m(v_k,v)v_k$, which is the orthogonal projection of H and V in $V_m:=span[v_1,\dots ,v_m]$ with their respective norms.

Denote $u^m(t)={\sum }_{k=1}^m{\eta }_{mk}(t)v_k$, where ${\eta }_{mk}(t)=(u^m(t),v_k)$, $k=1,2,\dots ,m$, are unknown real functions satisfying the finite-dimensional problem

$$\{\begin{array}{l}(u^m,v_k)+{\alpha }^2({\mathit{Au}}^m(t),v_k)+\nu {\int }_0^t〈{\mathit{Au}}^m(s),v_k〉ds+{\int }_0^t〈B(u^m(s),u^m(s)),v_k〉ds\\ =(u_0,v_k)+{\alpha }^2({\mathit{Au}}_0,v_k)+{\int }_0^t(g(s,u^m(s-\rho (s))),v_k)ds,t>0,\mathrm{\forall }1\le k\le m,\\ u^m(t)={\phi }^m(t),\text{a.e. }t\in (-h,0),\end{array}$$

(3.4)

with ${\phi }^m(t)=P_m\phi (t)$. From [12], we can obtain the local well-posedness of this finite-dimensional delay problem. The following provides estimates which imply that the solutions are well defined in the whole $[0,+\mathrm{\infty })$.

By (3.4), we obtain

$$\begin{array}{r}\frac{d}{dt}((u^m,v_k)+{\alpha }^2({\mathit{Au}}^m(t),v_k))+\nu 〈{\mathit{Au}}^m(t),v_k〉+B(u^m(t),u^m(t)),v_k〉\\ =(g(t,u^m(t-\rho (t))),v_k),t>0,\mathrm{\forall }1\le k\le m.\end{array}$$

(3.5)

Multiplying (3.5) by $(u^m(t),v_k)$, summing from $k=1$ to $k=m$, and using the properties of the operator b, we easily get

$$\frac{d}{dt}({|u^m(t)|}^2+{\alpha }^2{\parallel u^m(t)\parallel }^2)+2\nu {\parallel u^m(t)\parallel }^2=2〈g(t,u^m(t-\rho (t))),u^m(t)〉.$$

(3.6)

Observing (H3) and using the Young inequality, we have

$$\begin{array}{r}2〈g(t,u^m(t-\rho (t))),u^m(t)〉\\ \le 2{\parallel g(t,u(t-\rho (t)))\parallel }_{V^{\prime }}\parallel u^m(t)\parallel \\ \le 2({\gamma }^{\frac{1}{2}}(t)\parallel u^m(t-\rho (t))\parallel +{\beta }^{\frac{1}{2}}(t))\parallel u^m(t)\parallel \\ =2{\gamma }^{\frac{1}{2}}(t)\parallel u^m(t-\rho (t))\parallel \parallel u^m(t)\parallel +2{\beta }^{\frac{1}{2}}(t)\parallel u^m(t)\parallel \\ \le \nu (1-{\rho }_0){\parallel u^m(t-\rho (t))\parallel }^2+\frac{\gamma (t)}{\nu (1-{\rho }_0)}{\parallel u^m(t)\parallel }^2+\beta (t)+{\parallel u^m(t)\parallel }^2\\ =\nu (1-{\rho }_0){\parallel u^m(t-\rho (t))\parallel }^2+(1+\frac{\gamma (t)}{\nu (1-{\rho }_0)}){\parallel u^m(t)\parallel }^2+\beta (t).\end{array}$$

(3.7)

Considering the above inequality in (3.6) and observing that

$$\begin{array}{rcl}{\int }_0^t{\parallel u^m(s-\rho (s))\parallel }^{2}ds& \le & \frac{1}{1-{\rho }_0}{\int }_{-\rho (0)}^{t-\rho (t)}{\parallel u^m(s)\parallel }^{2}ds\\ \le & \frac{1}{1-{\rho }_0}({\int }_{-h}^0{\parallel \phi (s)\parallel }^{2}ds+{\int }_0^t{\parallel u^m(s)\parallel }^{2}ds),\end{array}$$

(3.8)

we easily get

$$\begin{array}{r}{|u^m(t)|}^2+{\alpha }^2{\parallel u^m(t)\parallel }^2+2\nu {\int }_0^t{\parallel u^m(s)\parallel }^{2}ds\\ \le {|u_0|}^2+{\alpha }^2(t){\parallel u_0\parallel }^2+{\int }_0^T\beta (s)ds+\nu {\int }_{-h}^0{\parallel \phi (s)\parallel }^{2}ds\\ +{\int }_0^t(1+\nu +\frac{\gamma (t)}{\nu (1-{\rho }_0)}){\parallel u^m(s)\parallel }^{2}ds.\end{array}$$

(3.9)

From the above inequality and the Gronwall inequality, one has that $\{u^m\}$ is bounded in $L^2(0,T;V)$, also in $L^{\mathrm{\infty }}(0,T;V)$, for any $T>0$. Observing (3.5), we know that the sequence ${\{\frac{d{u}^m}{dt}\}}_{m\ge 1}$ is bounded in $L^2(0,T;V^{\prime })$ for all $T>0$. The reason is the same as in [12].

By the compactness of the injection of V into H, using the above estimates and the Ascoli-Arzelà theorem, we deduce that there exist a subsequence ${\{u^m\}}_{m\ge 1}$ (we relabel the same) and $u\in W^{1,2}(0,T;V)\cap L^{2q}(-h,T;V)$ for any $T>0$ with $u=\phi$ in $(-h,0)$. Recalling (3.9) and the above analysis, we have

$$u^m\stackrel{\ast }{\rightharpoonup }u\text{weakly-star in }{L}^{\mathrm{\infty }}(0,T;V),$$

(3.10)

$u^m\to u$ strongly in $C(0,T;H)$ for all $T>0$, and

$$u^m(t)\to u(t),\text{a.e. }t>0\text{ in }V.$$

(3.11)

By the properties of operator A and (3.10), we deduce that ${\mathit{Au}}^m\rightharpoonup \mathit{Au}$ weakly in $L^2(0,T;V^{\prime })$. Reasoning as in [26] on page 76, we deduce that $B(u^m)\rightharpoonup B(u)$ weakly in $L^2(0,T;V^{\prime })$ for any $T>0$.

On the other hand, observing that by (3.11), (H2) and the hypothesis on ρ in (3.1), for any time t, we conclude for any $T>0$

$$g(t,u^m(t-\rho (t)))\to g(t,u(t-\rho (t)))\text{in }V\text{ a.e. }0<t<T$$

(3.12)

and as $\{u^m\}$ is bounded in the space $L^{\mathrm{\infty }}(0,T;V^{\prime })$ obtained from (3.9), by (H3), we deduce

$${\parallel g(t,u^m(t-\rho (t)))\parallel }_{V^{\prime }}^2\le \{\begin{array}{ll}\beta (t)+\gamma (t),& t>\rho (t),\\ \beta (t)+\gamma (t){\parallel \phi (t-\rho (t))\parallel }^2,& t<\rho (t),\end{array}$$

(3.13)

where $C={sup}_{m\ge 1}{\parallel u^m\parallel }_{L^{\mathrm{\infty }}(0,T;V)}$. Thus we can easily derive from (3.12) and (3.13)

$$g(t,u^m(t-\rho (t)))\to g(t,u(t-\rho (t)))\text{in }{L}^2(0,T;V^{\prime }).$$

(3.14)

From the above discussion, passing to the limit, we prove that u is a global solution of (3.2) in the sense of Definition 3.1. □

Remark 3.1 We can obtain the uniqueness if there are additional assumptions on the forcing term g. For example, if we suppose that g satisfies (H1), (H3), for an arbitrary $T>\tau$ and $C_T=C_1{max}_{t\in [\tau ,T]}(\parallel u(t)\parallel ,\parallel v(t)\parallel )>0$, then for the solutions u, v,

$${\parallel g(t,u)-g(t,v)\parallel }_{V^{\prime }}\le (\nu +C_T)\parallel u-v\parallel ,$$

then we obtain the uniqueness of solutions.

4 Existence of pullback attractors

In this section, we discuss the existence of pullback attractors for the 3D Navier-Stokes-Voight equations with delays in continuous and sub-linear operators. At first, we propose the assumptions for g given in Section 3:

(H1^′) For all $u\in V$, $g(\cdot ,u):\mathbb{R}\to H$ is measurable.

(H2^′) For all $t\in \mathbb{R}$, $g(t,\cdot ):H\to H$ is continuous.

(H3^′) There are two nonnegative functions $\gamma (t),\beta (t):\mathbb{R}\to [0,+\mathrm{\infty })$ with $\gamma (t)\in L_{loc}^p(\mathbb{R})$ for some $1\le p\le +\mathrm{\infty }$ and $\beta (t)\in L_{loc}^1(\mathbb{R})$ such that for any $u\in V$,

$${\parallel g(t,u)\parallel }_{V^{\prime }}^2\le \gamma (t){\parallel u\parallel }^2+\beta (t)\text{for any }t\in \mathbb{R}.$$

To construct a multi-valued process, we introduce symbols $C_V=C([-h,0];V)$ and $S_V^{2q}=V\times L^{2q}(-h,0;V)$, where $\frac{1}{p}+\frac{1}{q}=1$ as two phase spaces. Let $D(\tau ,u_0,\phi )$ denote the set of global solutions of (1.1) in $[\tau ,+\mathrm{\infty })$ and the initial datum $(u_0,\phi )\in S_V^{2q}$.

By Theorem 3.1, we know there exists a solution to problem (3.2) although we have no discussion on the uniqueness of solutions to problem (3.2). We may define two strict processes, $(C_V,\{U(\cdot ,\cdot )\})$ as

$$U(t,\tau )\phi =\{u(t):u\in D(\tau ,\phi (0),\phi )\}\text{for any }\phi \in C_V,$$

and $(S_V^{2q},\{U(\cdot ,\cdot )\})$ as

$$U(t,\tau )(u_0,\phi )=\{u(t):u\in D(\tau ,u^0,\phi )\}\text{for any }(u_0,\phi )\in S_V^{2q}.$$

Considering the regularity of the problem, the asymptotic behavior of the two processes shall be the same, as we shall see in what follows.

In order to simplify the calculation form, we introduce a function ${\kappa }_{\sigma }$. For any $\sigma >0$, we set

$${\kappa }_{\sigma }(t,s)=(d-\frac{\sigma +d}{{\alpha }^2})(t-s)-\frac{e^{dh}}{{\alpha }^{2}d(1-{\rho }_0)}{\int }_s^t\gamma (r)dr,\mathrm{\forall }t,s\in \mathbb{R}.$$

(4.1)

From (4.1), we can find that

$$-{\kappa }_{\sigma }(t,s)={\kappa }_{\sigma }(0,t)-{\kappa }_{\sigma }(0,s),\mathrm{\forall }t,s\in \mathbb{R},$$

(4.2)

and for any σ: $0<\sigma <{\alpha }^{2}d-d$, then

$${\kappa }_{\sigma }(0,r)\le {\kappa }_{\sigma }(0,t)+(d-\frac{\sigma +d}{{\alpha }^2})h,\mathrm{\forall }r\in [t-h,t],$$

(4.3)

where $d=\nu min\{{\lambda }_1,\frac{1}{{\alpha }^2}\}$.

Lemma 4.1 Suppose that (H1′)-(H3′) hold, for any initial datum $(u_0,\phi )\in S_V^{2q}$ and any $u\in D(\tau ,u_0,\phi )$, it holds

$${\parallel u(t)\parallel }^2\le \frac{1}{{\alpha }^2}{C}_{\tau }{e}^{-{\kappa }_{\sigma }(t,\tau )}+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{\tau }^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds,$$

(4.4)

where $C_{\tau }=d{\int }_{-h}^0{e}^{dr}{\parallel \phi (r)\parallel }^{2}dr+{|u_0|}^2+{\alpha }^2{\parallel u_0\parallel }^2$.

Proof Let u be a solution of (3.2), so $u\in D(\tau ,u_0,\phi )$. Multiplying (1.1) by $u(t)$ and using the energy equality and the Poincaré inequality, we have

$$\begin{array}{r}\frac{d}{dt}({|u(t)|}^2+{\alpha }^2{\parallel u(t)\parallel }^2)+d({|u(t)|}^2+{\alpha }^2{\parallel u(t)\parallel }^2)\\ \le 2{\parallel g(t,u(t-\rho (t)))\parallel }_{V^{\prime }}{\parallel u(t)\parallel }_V,\end{array}$$

where $d=\nu min\{{\lambda }_1,\frac{1}{{\alpha }^2}\}$. Thus

$$\begin{array}{r}\frac{d}{dt}\left[e^{dt}({|u(t)|}^2+{\alpha }^2{\parallel u(t)\parallel }^2)\right]\\ \le 2e^{dt}{\parallel g(t,u(t-\rho (t)))\parallel }_{V^{\prime }}{\parallel u(t)\parallel }_V\\ \le 2e^{dt}({\gamma }^{\frac{1}{2}}(t)\parallel u(t-\rho (t))\parallel +{\beta }^{\frac{1}{2}}(t))\parallel u(t)\parallel \\ \le 2e^{dt}{\gamma }^{\frac{1}{2}}(t)\parallel u(t)\parallel \parallel u(t-\rho (t))\parallel +2e^{dt}{\beta }^{\frac{1}{2}}(t)\parallel u(t)\parallel \\ \le C_0^{-1}{e}^{dt}{\parallel u(t-\rho (t))\parallel }^2+(C_0\gamma (t)+\sigma )e^{dt}{\parallel u(t)\parallel }^2+{\sigma }^{-1}{e}^{dt}\beta (t),\end{array}$$

(4.5)

where we have denoted

$$C_0=\frac{e^{dh}}{d(1-{\rho }_0)}.$$

Considering

$$\begin{array}{rl}{\int }_{\tau }^t{e}^{ds}{\parallel u(s-\rho (s))\parallel }^{2}ds& \le \frac{e^{dh}}{1-{\rho }_0}\left({\int }_{\tau -h}^t{e}^{dr}\parallel u(r)\parallel dr\right)\\ =\frac{e^{dh}}{1-{\rho }_0}(e^{d\tau }{\int }_{-h}^0{e}^{dr}{\parallel \phi (r)\parallel }^{2}dr+{\int }_{\tau }^t{e}^{dr}{\parallel u(r)\parallel }^{2}dr),\end{array}$$

(4.6)

and integrating (4.5) from τ to t, we deduce

$$\begin{array}{r}{e}^{dt}{|u(t)|}^2+{\alpha }^2{e}^{dt}{\parallel u(t)\parallel }^2\\ \le C_0^{-1}{\int }_{\tau }^t{e}^{ds}{\parallel u(s-\rho (s))\parallel }^{2}ds+{\int }_{\tau }^t(C_0\gamma (s)+\sigma )e^{ds}{\parallel u(s)\parallel }^{2}ds+{\sigma }^{-1}{\int }_{\tau }^t\beta (s)ds\\ +e^{d\tau }{|u_0|}^2+{\alpha }^2{e}^{d\tau }{\parallel u_0\parallel }^2\\ \le C_0^{-1}\times \frac{e^{dh}}{1-{\rho }_0}\times e^{d\tau }{\int }_{-h}^0{e}^{dr}{\parallel \phi (r)\parallel }^{2}dr+C_0^{-1}\times \frac{e^{dh}}{1-{\rho }_0}{\int }_{\tau }^t{e}^{dr}{\parallel u(r)\parallel }^{2}dr\\ +{\int }_{\tau }^t(C_0\gamma (s)+\sigma )e^{ds}{\parallel u(s)\parallel }^{2}ds+{\sigma }^{-1}{\int }_{\tau }^t{e}^{ds}\beta (s)ds+e^{d\tau }{|u_0|}^2+{\alpha }^2{e}^{d\tau }{\parallel u_0\parallel }^2\\ =d{e}^{d\tau }{\int }_{-h}^0{e}^{dr}{\parallel \phi (r)\parallel }^{2}dr+{\int }_{\tau }^t{e}^{ds}(C_0\gamma (s)+\sigma +d){\parallel u(s)\parallel }^{2}ds\\ +{\sigma }^{-1}{\int }_{\tau }^t{e}^{dr}\beta (r)dr+e^{d\tau }{|u_0|}^2+{\alpha }^2{e}^{d\tau }{\parallel u_0\parallel }^2,\end{array}$$

(4.7)

where we set

$$C_{\tau }=d{\int }_{-h}^0{e}^{ds}{\parallel \phi (s)\parallel }^{2}ds+{|u_0|}^2+{\alpha }^2{\parallel u_0\parallel }^2.$$

Observing the above estimates, we easily deduce

$$\begin{array}{r}{e}^{dt}{|u(t)|}^2+{\alpha }^2{e}^{dt}{\parallel u(t)\parallel }^2\\ \le e^{d\tau }{C}_{\tau }+{\int }_{\tau }^t(C_0\gamma (s)+\sigma +d)e^{dr}{\parallel u(r)\parallel }^{2}dr+{\sigma }^{-1}{\int }_{\tau }^t{e}^{dr}\beta (r)dr.\end{array}$$

(4.8)

Applying the Poincaré inequality and the Gronwall inequality to (4.8), we deduce that (4.4) holds. This finishes the proof of this lemma. □

Next, we shall prove that the processes $(C_V,\{U(\cdot ,\cdot )\})$ and $(S_V^{2q},\{U(\cdot ,\cdot )\})$ defined above are pullback-absorbing. To obtain this, we propose the assumptions (H4′)

$$\underset{t\to -\mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{1}{t}{\int }_0^t\gamma (s)ds=\overline{\gamma }\in [0,+\mathrm{\infty }),$$

and the relation among constants $\sigma >0$, d defined above, and α in (1.1) satisfies(H5′)

$$d-\frac{\sigma +d}{{\alpha }^2}-\frac{C_0}{{\alpha }^2}>0,$$

and $\beta (t)$ satisfies

(H6^′)

$${\int }_{-\mathrm{\infty }}^0{e}^{-{\kappa }_{\sigma }(0,r)}\beta (r)dr<+\mathrm{\infty },$$

where the function ${\kappa }_{\sigma }(t,s)$ is given by (4.1).

Before proving that the two multi-valued processes possess pullback-absorbing sets, we introduce the definition of the two natural tempered universes which shall play the key role for our main purpose.

Definition 4.1 Suppose that ${\mathcal{R}}_{\sigma }(t)$ is the collection of the sets of all functions $r:\mathbb{R}\to [0,+\mathrm{\infty })$ such that

$$\underset{t\to -\mathrm{\infty }}{lim}{e}^{-{\kappa }_{\sigma }(0,t)}{r}^2(t)=0.$$

Let ${\mathcal{D}}_{S_V^{2q}}$ be the class of all families $\hat{D}=\{D(t):t\in \mathbb{R}\}\subset \mathcal{P}(S_V^{2q})$ such that $D(t)\subset {\overline{B}}_{S_V^{2q}}(0,r_{\hat{D}}(t))$ for some $r_{\hat{D}}\in {\mathcal{R}}_{\sigma }$. In the same way, let ${\mathcal{D}}_{C_V}^{\sigma }$ denote the class of all families $\hat{D}=\{D(t):t\in \mathbb{R}\}\subset \mathcal{P}(C_V)$ satisfying $D(t)\subset {\overline{B}}_{C_V}(0,r_{\hat{D}}(t))$ for some $r_{\hat{D}}\in {\mathcal{R}}_{\sigma }$.

Let $B_0$ be any fixed bounded subset of $S_V^{2q}$. Observing that ${\mathcal{D}}_{C_V}^{\sigma }\subset {\mathcal{D}}_{S_V^{2q}}$, which is inclusion-closed, by (H4^′) and (H5^′), we deduce that the family $\hat{B}=\{B(t)\equiv B_0,t\in \mathbb{R}\}$ is contained in ${\mathcal{D}}_{S_V^{2q}}^{\sigma }$. With regard to ${\mathcal{D}}_{C_V}$, we use the same method and obtain a similar conclusion if $B_0$ is included in $C_V$.

The following lemma provides that there exist pullback-absorbing sets for the two processes mentioned above.

Lemma 4.2 Suppose that (H1^′)-(H6^′) hold and the constants α, d, $C_0$, $\overline{\gamma }$ satisfy $d-\frac{\sigma +d}{{\alpha }^2}-\frac{C_0}{{\alpha }^2}\overline{\gamma }>0$ and $\overline{\gamma }<1$.

• (1) Then, for any $t\in \mathbb{R}$ and any family $\hat{B}=\{B(t):t\in \mathbb{R}\}$, there exits $\tau (\hat{B},t)\le t$ such that any initial datum $(u_0,\phi )\in S_V^{2q}$ and any $u\in D(\tau ,u_0,\phi )$ for any $\tau \le \tau (\hat{B},t)$ satisfy that $\parallel u(t)\parallel \le R_V(t)$, where the positive continuous function $R_V(\cdot )$ is given by

  $$R_V^2(t)=1+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{\tau }^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds,\mathrm{\forall }t\in \mathbb{R}.$$

• (2) Let ${\hat{D}}_0=\{D_0(t):t\in \mathbb{R}\}$ be included $\mathcal{P}(C_V)$ which is given by

  $$D_0(t)={\overline{B}}_{C_V}(0,{\tilde{R}}_V(t))\mathit{\text{and}}{\tilde{R}}_V(t)=\underset{t-h\le r\le t}{max}{R}_V(r),\mathrm{\forall }t\in \mathbb{R}.$$

Then the set ${\hat{D}}_0\in {\mathcal{D}}_{C_V}^{\sigma }$ and is ${\mathcal{D}}_{S_V^{2q}}^{\sigma }$-pullback absorbing for the process $(S_V^{2q},U)$. Therefore, ${\hat{D}}_0$ is ${\mathcal{D}}_{C_V}^{\sigma }$-pullback absorbing for the process $(C_V,U)$.

Proof Since the proof is a consequence of the definition of ${\mathcal{D}}_{S_V^{2q}}$, we only sketch it here. From Lemma 4.1, (H5^′) and (H6^′) , we have

$$\begin{array}{rcl}{\parallel u(t)\parallel }^2& \le & \frac{1}{{\alpha }^2}{C}_{\tau }{e}^{-{\kappa }_{\sigma }(t,\tau )}+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{\tau }^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds\\ =& \frac{1}{{\alpha }^2}{C}_{\tau }{e}^{{\kappa }_{\sigma }(0,t)}\cdot e^{-\kappa (0,\tau )}+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{\tau }^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds\\ =& \frac{1}{{\alpha }^2}{C}_{\tau }{e}^{-{\kappa }_{\sigma }(0,t)}\cdot e^{(d-\frac{\sigma +d}{{\alpha }^2})\tau -\frac{C_0}{{\alpha }^2}{\int }_0^{\tau }\gamma (r)dr}+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{\tau }^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds\\ \le & \frac{C_{\tau }}{{\alpha }^2}{e}^{{\kappa }_{\sigma }(0,t)}{e}^{(d-\frac{\sigma +d}{{\alpha }^2}-\frac{C_0}{{\alpha }^2})\tau }+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{\tau }^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds\\ \le & 1+\frac{1}{{\alpha }^2}{\sigma }^{-1}{\int }_{-\mathrm{\infty }}^t{e}^{-{\kappa }_{\sigma }(t,s)}\beta (s)ds.\end{array}$$

(4.9)

We complete the proof of (1). Estimate (2) is a consequence of (1). □

For the two processes $(S_V^{2q},U)$ and $(C_V,U)$, they possess pullback-absorbing sets. In order to apply Lemma 2.3 to obtain the existence of pullback attractors, it is necessary to prove that the two multi-valued processes are asymptotically compact. This will be done in the following lemma.

Lemma 4.3 Suppose that the assumptions in Lemma  4.2 hold. The two processes $(C_V,U)$ and $(S_V^{2q},U)$ are ${\hat{D}}_0$-asymptotically compact.

Proof For any $t_0\in \mathbb{R}$ , a sequence $\{{\tau }_n\}\subset (-\mathrm{\infty },t_0-2h]$ with ${\tau }_n\to -\mathrm{\infty }$ and a sequence $\{u^n\}$ with $u^n\in D({\tau }_n,{\phi }_n(0),{\phi }_n)$ with ${\phi }_n\in D_0({\tau }_n)$, we shall prove that the sequence $\{u_{t_0}^n\}$ is relatively compact in $C_V$. By the properties concerning operator b mentioned in Section 3, we deduce that

$${\parallel {\left(u^n\right)}^{\prime }\parallel }_{V^{\prime }}+{\alpha }^2\parallel {\left(u^n\right)}^{\prime }\parallel \le \nu \parallel u^n\parallel +{\parallel b(u^n,u^n,\cdot )\parallel }_{V^{\prime }}+{\parallel g(t,u^n(t-\rho (t)))\parallel }_{V^{\prime }}.$$

It is easy to get the above estimate which is independent of n. The sequences of $\{u^n\}$ and $\{{(u^n)}^{\prime }\}$ possess their subsequence, relabeled the same in suitable spaces such that there exist $u\in L^{\mathrm{\infty }}(t_0-2h;V)$ and $u^{\prime }\in L^2(t_0-h,t_0;V^{\prime })$ satisfying

$$\{\begin{array}{ll}{u}^n\stackrel{\ast }{\rightharpoonup }u& \text{weakly-star in }{L}^{\mathrm{\infty }}(t_0-2h,t_0;V),\\ u^n\rightharpoonup u& \text{weakly in }{L}^2(t_0-2h,t_0;V),\\ \frac{d}{dt}{u}^n\rightharpoonup \frac{d}{dt}u& \text{weakly in }{L}^2(t_0-h,t_0;V^{\prime }),\\ u^n(r)\to u(r)& \text{strongly in }V\text{ a.e. }r\in (t_0-2h,t_0).\end{array}$$

(4.10)

According to the assumptions on a function g and analogously as in Theorem 3.1, we deduce that $g(r,u^n(r-\rho (r)))\to g(r,u(r-\rho (r)))$ strongly in V a.e. $r\in (t_0-h,t_0)$.

By the Lebesgue theorem and the uniform estimate of $u^n$ in $L^{\mathrm{\infty }}(t_0-2h,t_0;V)$, we deduce that the function $g(r,u^n(r-\rho (r)))$ converges to the function $g(r,u(r-\rho (r)))$ strongly. Therefore, for any $t\in [t_0-h,t_0]$, we have $u\in C([t_0-h,t_0];V)$ and

$$\begin{array}{r}u(t)+{\alpha }^2\mathit{Au}(t)+{\int }_{t_0-h}^t(\nu \mathit{Au}(r)+B(u(r)))dr\\ =u(t_0-h)+{\alpha }^2\mathit{Au}(t_0-h)+{\int }_{t_0-h}^{t}g(r,u(r-\rho (r)))dr.\end{array}$$

(4.11)

The uniform estimate of $\{{(u^n)}^{\prime }\}$ in $L^2(t_0-h,t_0;V^{\prime })$ implies that the sequence $\{u^n\}$ is equicontinuous in $V^{\prime }$ for any $t_0-h\le t\le t_0$. In addition, the sequence $\{u^n\}$ is bounded, which is independent of n in $C([t_0-h,t_0];V)$. Using the Ascoli-Arzelà theorem, we can obtain

$$u^n\to u\text{strongly in }C([t_0-h,t_0];V^{\prime }).$$

(4.12)

From the uniform boundedness of the sequence $\{u^n\}$ in $C([t_0-h,t_0];V)$, for any $r\in [t_0-h,t_0]$, we can also obtain $u^n(r)\rightharpoonup u(r)$, weakly in V.

By the analogous argument, for any compact sequence $\{r_n\}\subset [t_0-h,t_0]$ and $\{r_n\}\to r\in [t_0-h,t_0]$, we obtain that the sequence $\{u^n(r_n)\}$ is convergent to $u(r)$ weakly in V. To achieve our result in Lemma 4.3, we only need to prove

$$u^n\to u\text{strongly in }C([t_0-h,t_0];V).$$

The proof is slightly different from Proposition 6 in [20] or in [22]. We only sketch it here. We use a contradiction argument. Suppose that it is not true, then there would exist a value ε, a sequence (relabeled the same) $\{r_n\}\subset [r_n-h,t_0]$, and $r^{\prime }\in [t_0-h,t_0]$ with $r_n\to r^{\prime }$ satisfying $\parallel u^n(r_n)-u(r^{\prime })\parallel \ge \epsilon$ for all $n\ge 1$. We shall see $u^n(r_n)\to u(r^{\prime })$ in V. In order to achieve the last claim, because the sequence $\{u^n(r_n)\}$ is weakly convergent to $u(r)$ in V, we only need the convergence of the norms above. In other words, $\parallel u^n(r_n)\parallel \to \parallel u(r^{\prime })\parallel$ as $n\to \mathrm{\infty }$.

From the weak convergence of $u^n(r_n)$ in V, we get

$$\parallel u\left(r^{\prime }\right)\parallel \le \underset{n\to +\mathrm{\infty }}{lim}inf\parallel u^n\left(r^{\prime }\right)\parallel .$$

Therefore we have to check that

$$\underset{n\to +\mathrm{\infty }}{lim}sup\parallel u^n(r_n)\parallel \le \parallel u\left(r^{\prime }\right)\parallel .$$

(4.13)

From the energy equality, for any $t_0-h\le r\le t\le t_0$, we obtain

$$\begin{array}{r}\frac{1}{2}{|z(t)|}^2+\frac{1}{2}{\parallel z(t)\parallel }^2+\nu {\int }_r^t{\parallel z(s)\parallel }^{2}ds\\ =\frac{1}{2}{|z(r)|}^2+\frac{1}{2}{\parallel z(r)\parallel }^2+{\int }_r^t\left(g(s,z(s-\rho (s)))\right)ds,\end{array}$$

(4.14)

where $z=u$ or $z=u^n$. For any $t\in [t_0-h,t_0]$, define the continuous functions $J(t)$ and $J_n(t)$ as

$$\begin{array}{c}J(t)=\frac{1}{2}{|u(t)|}^2+\frac{1}{2}{\parallel u(t)\parallel }^2-{\int }_{t_0-h}^t(g(s,u(s-\rho (s))),u(s))ds,\hfill \\ J_n(t)=\frac{1}{2}{|u^n(t)|}^2+\frac{1}{2}{\parallel u^n(t)\parallel }^2-{\int }_{t_0-h}^t(g(s,u^n(s-\rho (s))),u^n(s))ds.\hfill \end{array}$$

By (4.14), it is clear that J and $J_n$ are non-increasing functions. By the convergence (4.10), for any $t\in (t_0-h,t_0)$, we have that $J_n(t)\to J(t)$. Using the same analysis method as in [22], we can deduce that for $n\ge n({\kappa }_{\epsilon })$, $J_n(r_n)-J(r^{\prime })\le \epsilon$, which gives (4.13) as desired. □

We can apply the technical method for any family in ${\mathcal{D}}_{S_V^{2q}}^{\sigma }$ in Lemma 4.3. Suppose that the assumptions in Lemma 4.3 hold. We can deduce that the processes $(C_V,U)$ and $(S_V^{2q},U)$ are ${\mathcal{D}}_{C_V}^{\sigma }$-asymptotically compact and ${\mathcal{D}}_{S_V^{2q}}^{\sigma }$-asymptotically compact.

Lemma 4.4 Suppose that (H1′)-(H6′) hold. The two processes $(C_V,U)$ and $(S_V^{2q},U)$ are semi-continuous and that $U(t,\tau ):S_V^{2q}\to \mathcal{P}(S_V^{2q})$ and $U(t,\tau ):C_V\to \mathcal{P}(C_V)$ have compact values in their respective topologies.

Proof In fact, the upper semi-continuity of the process $(S_V^{2q},U)$ can be obtained by similar arguments to those used for the Galerkin sequence in Theorem 3.1.

As to the process $(C_V,U)$, applying the same energy-procedure in Lemma 4.3, we shall obtain that in $[\tau ,t]$ any set of solutions possesses a converging subsequence in this process, whence the assertion in Lemma 4.4 follows. □

According to the results in Section 2, the following two theorems shall be obtained, which are our result in this paper. Observing Lemmas 4.3 and 4.4, and applying Lemma 2.6, we obtain the following theorem.

Theorem 4.1 Suppose that (H1′)-(H6′) hold. For any $t\in \mathbb{R}$, then there exist global pullback attractors ${\mathcal{A}}_{C_V}=\{{\mathcal{A}}_{C_V}(t)\}$ and ${\mathcal{A}}_{{\mathcal{D}}_{C_V}^{\sigma }}=\{{\mathcal{A}}_{{\mathcal{D}}_{C_V}^{\sigma }}(t)\}$ for the process $(C_V,U)$ in the universe of fixed bounded sets and in ${\mathcal{D}}_{C_V}^{\sigma }$, respectively. Moreover, they are unique in the sense of Lemma  2.5 and negatively and strictly invariant for U respectively, and the following holds:

$${\mathcal{A}}_{C_V}(t)\subset {\mathcal{A}}_{{\mathcal{D}}_{C_V}^{\sigma }}(t).$$

The above theorem proves that there exist pullback attractors in the $C_V$ framework, while we shall prove that there exist pullback attractors in the $S_V^{2q}$ framework in the following theorem.

Theorem 4.2 Suppose that the assumptions in Theorem  4.1 hold. For any $t\in \mathbb{R}$, there exist global pullback attractors ${\mathcal{A}}_{S_V^{2q}}=\{{\mathcal{A}}_{S_V^{2q}}(t)\}$ and ${\mathcal{A}}_{{\mathcal{D}}_{S_V^{2q}}^{\sigma }}=\{{\mathcal{A}}_{{\mathcal{D}}_{S_V^{2q}}^{\sigma }}(t)\}$ for the process $(S_V^{2q},U)$ in the universes of fixed bounded sets and in ${\mathcal{D}}_{S_V^{2q}}^{\sigma }$. They are unique in the sense of Lemma  2.5 and negatively and strictly invariant for U, respectively, and we have ${\mathcal{A}}_{S_V^{2q}}(t)\subset {\mathcal{A}}_{{\mathcal{D}}_{S_V^{2q}}^{\sigma }}(t)$. Moreover, the relationship between the attractors for $(S_V^{2q},U)$ and for $(C_V,U)$ is as follows:

$${\mathcal{A}}_{S_V^{2q}}(t)=f({\mathcal{A}}_{C_V}(t))\mathit{\text{and}}{\mathcal{A}}_{{\mathcal{D}}_{S_V^{2q}}^{\sigma }}(t)=f({\mathcal{A}}_{{\mathcal{D}}_{C_V}^{\sigma }}(t)),$$

(4.15)

where $f:C_V\to S_V^{2q}$ is the continuous mapping defined by $f(\phi )=(\phi (0),\phi )$.

Proof The proof is rather similar to that of Theorem 5 in [20]. Since the regularity is different from [20], we only sketch the proof of (4.15) here.

By Theorem 3.1, we can conclude that $U(t,\tau )$ maps $S_V^{2q}$ into bounded sets in $C_V$ if $t\ge \tau +h$, and also maps bounded sets from $S_V^{2q}$ into bounded sets of $C_V$.

Noting that ${\mathcal{A}}_{S_V^{2q}}(t)$ is the minimal closed set, and using Lemma 2.5 and the above arguments, we deduce that $f({\mathcal{A}}_{C_V}(t))$ also attracts bounded sets in $S_V^{2q}$ in a pullback sense. Therefore the inclusion ${\mathcal{A}}_{S_V^{2q}}(t)\subset f({\mathcal{A}}_{C_V}(t))$ holds.

As to the opposite inclusion of the first identification in (4.15), for any bounded set B, it follows from the continuous injection $f(C_V)\subset S_V^{2q}$ and the attractor ${\mathcal{A}}_{C_V}(t)={\overline{{\bigcup }_B{\mathrm{\Lambda }}_{C_V}(B,t)}}^{C_V}$. Thus $f({\mathcal{A}}_{C_V}(t))={\overline{{\bigcup }_{B}f({\mathrm{\Lambda }}_{C_V}(B,t))}}^{C_V}$, whence the opposite inclusion of the first identification in (4.15) holds.

Analogously, it is obvious that the second relation in (4.15) holds. □