- Research Article
- Open access
- Published:
Extension Theorem for Complex Clifford Algebras-Valued Functions on Fractal Domains
Boundary Value Problems volume 2010, Article number: 513186 (2010)
Abstract
Monogenic extension theorem of complex Clifford algebras-valued functions over a bounded domain with fractal boundary is obtained. The paper is dealing with the class of Hölder continuous functions. Applications to holomorphic functions theory of several complex variables as well as to that of the so-called biregular functions will be deduced directly from the isotonic approach.
1. Introduction
It is well known that methods of Clifford analysis, which is a successful generalization to higher dimension of the theory of holomorphic functions in the complex plane, are a powerful tool for study boundary value problems of mathematical physics over bounded domains with sufficiently smooth boundaries; see [1–3].
One of the most important parts of this development is the particular feature of the existence of a Cauchy type integral whose properties are similar to its famous complex prototype. However, if domains with boundaries of highly less smoothness (even nonrectifiable or fractal) are allowed, then customary definition of the Cauchy integral falls, but the boundary value problems keep their interest and applicability. A natural question arises as follows.
Can we describe the class of complex Clifford algebras-valued functions from Hölder continuous space extending monogenically from the fractal boundary of a domain through the whole domain?
In [4] for the quaternionic case and in [5–7] for general complex Clifford algebra valued functions some preliminaries results are given. However, in all these cases the condition ensures that extendability is given in terms of box dimension and Hölder exponent of the functions space considered.
In this paper we will show that there is a rich source of material on the roughness of the boundaries permitted for a positive answer of the question which has not yet been exploited, and indeed hardly touched.
At the end, applications to holomorphic functions theory of several complex variables as well as to the so-called biregular functions (to be defined later) will be deduced directly from the isotonic approach.
The above motivation of our work is of more or less theoretical mathematical nature but it is not difficult to give arguments based on an ample gamma of applications.
Indeed, the M. S. Zhdanov book cited in [8] is a translation from Russian and the original title means literally "The analogues of the Cauchy-type integral in the Theory of Geophysics Fields". In this book is considered, as the author writes, one of the most interesting questions of the Potential plane field theory, a possibility of an analytic extension of the field into the domain occupied by sources.
He gives representations of both a gravitational and a constant magnetic field as such analogues in order to solve now the spatial problems of the separation of field as well as analytic extension through the surface and into the domain with sources.
Our results can be applied to the study of the above problems in the more general context of domains with fractal boundaries, but the detailed discussion of this technical point is beyond the scope of this paper.
2. Preliminaries
Let  be an orthonormal basis of the Euclidean space
be an orthonormal basis of the Euclidean space  .
.
The complex Clifford algebra, denoted by  , is generated additively by elements of the form
, is generated additively by elements of the form

where  is such that
is such that  , and so the complex dimension of
, and so the complex dimension of  is
is  . For
. For  ,
,  is the identity element.
is the identity element.
For  , the conjugation and the main involution are defined, respectively, as
, the conjugation and the main involution are defined, respectively, as

If we identify the vectors  of
of  with the real Clifford vectors
with the real Clifford vectors  , then
, then  may be considered as a subspace of
may be considered as a subspace of  .
.
The product of two Clifford vectors splits up into two parts:

where

Generally speaking, we will consider  -valued functions
-valued functions  on
on  of the form
of the form

where  are
are  -valued functions. Notions of continuity and differentiability of
-valued functions. Notions of continuity and differentiability of  are introduced by means of the corresponding notions for its complex components
are introduced by means of the corresponding notions for its complex components  .
.
In particular, for bounded set  , the class of continuous functions which satisfy the Hölder condition of order
, the class of continuous functions which satisfy the Hölder condition of order 
 in
in  will be denoted by
will be denoted by  .
.
Let us introduce the so-called Dirac operator given by

It is a first-order elliptic operator whose fundamental solution is given by

where  is the area of the unit sphere in
is the area of the unit sphere in  .
.
If  is open in
is open in  and
and  , then
, then  is said to be monogenic if
is said to be monogenic if  in
in  . Denote by
. Denote by  the set of all monogenic functions in
the set of all monogenic functions in  . The best general reference here is [9].
. The best general reference here is [9].
We recall (see [10]) that a Whitney extension of  ,
,  being compact in
being compact in  , is a compactly supported function
, is a compactly supported function  such that
such that  and
and

Here and in the sequel, we will denote by  certain generic positive constant not necessarily the same in different occurrences.
certain generic positive constant not necessarily the same in different occurrences.
The following assumption will be needed through the paper. Let  be a Jordan domain, that is, a bounded oriented connected open subset of
be a Jordan domain, that is, a bounded oriented connected open subset of  whose boundary
whose boundary  is a compact topological surface. By
is a compact topological surface. By  we denote the complement domain of
we denote the complement domain of  .
.
By definition (see [11]) the box dimension of  , denoted by
, denoted by  , is equal to
, is equal to  where
where  stands for the least number of
stands for the least number of  -balls needed to cover
-balls needed to cover  .
.
The limit above is unchanged if  is thinking as the number of
is thinking as the number of  -cubes with
-cubes with  intersecting
intersecting  . A cube
. A cube  is called a
is called a  -cube if it is of the form:
-cube if it is of the form:  where
where  are integers.
are integers.
Fix  , assuming that the improper integral
, assuming that the improper integral  converges. Note that this is in agreement with [12] for
converges. Note that this is in agreement with [12] for  to be
to be  -summable.
-summable.
Observe that a  -summable surface has box dimension
-summable surface has box dimension  . Meanwhile, if
. Meanwhile, if  has box dimension less than
has box dimension less than  , then
, then  is
is  -summable.
-summable.
3. Extension Theorems
We begin this section with a basic result on the usual Cliffordian Théodoresco operator defined by

If  such that
such that  , which we may assume, then it follows that
, which we may assume, then it follows that  and we may choose
and we may choose  such that
such that  . If for such
. If for such  we can prove that
we can prove that  then by in [3, Proposition
then by in [3, Proposition  ] it follows that
] it follows that  represents a continuous function in
represents a continuous function in  . Moreover,
. Moreover,  for any
for any  , which is due to the fact that
, which is due to the fact that  .
.
In the remainder of this section we assume that  .
.
3.1. Monogenic Extension Theorem
Theorem 3.1.
If  is the trace of
is the trace of  , then
, then

Conversely, assuming that (3.2) holds, then  is the trace of
is the trace of  , for any
, for any  .
.
Proof.
Let  and define
and define

and  .
.
Note that the boundary of  , denoted by
, denoted by  , is actually composed by certain faces (denoted by
, is actually composed by certain faces (denoted by  ) of some cubes
) of some cubes  . We will denote by
. We will denote by  ,
,  the outward pointing unit normal to
the outward pointing unit normal to  and
and  , respectively, in the sense introduced in [13].
, respectively, in the sense introduced in [13].
Let  and let
and let  be so large chosen that
be so large chosen that  and
and  for
for  , where
, where  is a cube of
is a cube of  . Here and below
. Here and below  denotes the diameter of
denotes the diameter of  as a subset of
as a subset of  .
.
Let  ,
,  a cube containing
a cube containing  , and
, and  such that
such that  .
.
Since  ,
,  , we have
, we have

Let  be an
be an  -dimensional face of
-dimensional face of  and
and  the
the  -cube containing
-cube containing  ; then if
; then if  , we have
, we have

Each face of  is one of those
is one of those  of some
of some  . Therefore, for
. Therefore, for 

Since  , we get
, we get

By Stokes formula we have

Therefore

The same conclusion can be drawn for  . The only point now is to note that
. The only point now is to note that  for
for  .
.
Finally, due to the fact that

we prove that  , and the second assertion follows directly by taking
, and the second assertion follows directly by taking  .
.
The finiteness of the last sum follows from the  -summability of
-summability of  together with the fact that
together with the fact that  .
.
For  the following analogous result can be obtained.
the following analogous result can be obtained.
Theorem 3.2.
Let  . If
. If  is the trace of
is the trace of  and
and  , then
, then

Conversely, assuming that (3.11) holds, then  is the trace of
is the trace of  , for any
, for any  .
.
3.2. Isotonic Extension Theorem
For our purpose we will assume that the dimension of the Euclidean space  is even whence we will put
is even whence we will put  from now on.
from now on.
In a series of recent papers, so-called isotonic Clifford analysis has emerged as yet a refinement of the standard case but also has strong connections with the theory of holomorphic functions of several complex variables and biregular ones, even encompassing some of its results; see [14–18].
Put

then a primitive idempotent is given by

We have the following conversion relations:

with  (complex Clifford algebra generated by
(complex Clifford algebra generated by  ).
).
Note that for  one also has that
one also has that

Let us introduce the following real Clifford vectors and their corresponding Dirac operators:

The function  is said to be isotonic in
is said to be isotonic in  if and only if
if and only if  is continuously differentiable in
is continuously differentiable in  and moreover satisfies the equation
and moreover satisfies the equation

We will denote by  the set of all isotonic functions in
the set of all isotonic functions in  .
.
We find ourselves forced to introduce two extra Cauchy kernels, defined by

Now we may introduce the isotonic Théodoresco transform of a function  to be
to be

It is straightforward to deduce that

Theorem 3.3.
If  , is the trace of
, is the trace of  , then
, then

Conversely, assuming that (3.21) holds, then  is the trace of
is the trace of  , for any
, for any  .
.
Proof.
Let  be an isotonic extension of
be an isotonic extension of  to
to  such that
such that  . Then,
. Then,  is a monogenic extension of
is a monogenic extension of  to
to  , which obviously belongs to
, which obviously belongs to  . Therefore
. Therefore

by Theorem 3.1.
We thus get

the first equality being a direct consequence of (3.20). According to (3.15) we have (3.21), which is the desired conclusion.
On account of Theorem 3.1 again, the converse assertion follows directly by taking  , and the proof is complete.
, and the proof is complete.
Remark 3.4.
Theorems 3.1 and 3.3 extend the results in [4–7], since the restriction putted there ( ) implies that of this paper.
) implies that of this paper.
4. Applications
In this last section, we will briefly discuss two particular cases which arise when considering (3.17).
Case 1.
It is easily seen that if  takes values in the space of scalars
takes values in the space of scalars  , then
, then  is isotonic if and only if
is isotonic if and only if

which means that  is a holomorphic function with respect to the
is a holomorphic function with respect to the  complex variables
complex variables  .
.
Case 2.
If  , isotonic function, takes values in the real Clifford algebra
, isotonic function, takes values in the real Clifford algebra  , then
, then

or, equivalently, by the action of the main involution on the second equation we arrive to the overdetermined system:

whose solutions are called biregular functions. For a detailed study we refer the reader to [19–21].
The proof of Theorem 3.3 may readily be adapted to establish analogous results for both holomorphic and biregular functions context. Clearly, we prove that if we replace  by a
by a  -valued, respectively,
-valued, respectively,  -valued function, such that (3.21) holds, then there exists an isotonic extension
-valued function, such that (3.21) holds, then there exists an isotonic extension  , which, by using the classical Dirichlet problem, takes values precisely in
, which, by using the classical Dirichlet problem, takes values precisely in  or
or  , respectively. On the other direction the proof is immediate. The corresponding statements are left to the reader.
, respectively. On the other direction the proof is immediate. The corresponding statements are left to the reader.
References
Gürlebeck K, Sprössig W: Quaternionic Analysis and Elliptic Boundary Value Problems, International Series of Numerical Mathematics. Volume 89. Birkhäuser, Basel, Switzerland; 1990:253.
Gürlebeck K, Sprössig W: Quaternionic and Clifford Calculus for Physicists and Engineers. John Wiley & Sons, New York, NY, USA; 1997.
Gürlebeck K, Habetha K, Sprössig W: Holomorphic Functions in the Plane and n-Dimensional Space. Birkhäuser, Basel, Switzerland; 2007.
Abreu-Blaya A, Bory-Reyes J, Moreno-García T:Holomorphic extension theorems in Lipschitz domains of
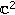 . Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0
. Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0Abreu-Blaya A, Bory-Reyes J, Peña DP, Sommen F: Biregular extendability via isotonic Clifford analysis. Mathematical Methods in the Applied Sciences 2010,33(4):384-393.
Abreu-Blaya R, Bory-Reyes J, Moreno-García T: Teodorescu transform decomposition of multivector fields on fractal hypersurfaces. In Wavelets, Multiscale Systems and Hypercomplex Analysis, Operator Theory: Advances and Applications. Volume 167. Birkhäuser, Basel, Switzerland; 2006:1-16. 10.1007/3-7643-7588-4_1
Abreu-Blaya R, Bory-Reyes J, Moreno-García T:A biregular extension theorem from a fractal surface in
 . to appear in Georgian Mathematical Journal
. to appear in Georgian Mathematical JournalShapiro M, Vasilievski NL, Zhdanov MS: Space analogs of the Cauchy type integrals and the quaternion theory. In Integral Transforms in Geophysics. Edited by: Zhdanov MS. Springer, Heidelberg, Germany; 1988:367. (Appendix A: 344–350)
Brackx F, Delanghe R, Sommen F: Clifford Analysis, Research Notes in Mathematics. Volume 76. Pitman, Boston, Mass, USA; 1982:x+308.
Stein EM: Singular Integrals and Differentiability Properties of Functions, Princeton Mathematical Series, no. 30. Princeton University Press, Princeton, NJ, USA; 1970:xiv+290.
Falconer KJ: The Geometry of Fractal Sets, Cambridge Tracts in Mathematics. Volume 85. Cambridge University Press, Cambridge, UK; 1986:xiv+162.
Harrison J, Norton A: The Gauss-Green theorem for fractal boundaries. Duke Mathematical Journal 1992,67(3):575-588. 10.1215/S0012-7094-92-06724-X
Federer H: Geometric Measure Theory, Die Grundlehren der mathematischen Wissenschaften. Volume 153. Springer, New York, NY, USA; 1969:xiv+676.
Abreu-Blaya R, Bory-Reyes J: A Martinelli-Bochner formula on fractal domains. Archiv der Mathematik 2009,92(4):335-343. 10.1007/s00013-009-3049-x
Abreu-Blaya R, Bory-Reyes J, Peña Peña D, Sommen F: The isotonic Cauchy transform. Advances in Applied Clifford Algebras 2007,17(2):145-152. 10.1007/s00006-007-0025-z
Abreu-Blaya A, Bory-Reyes J, Peña DP, Sommen F:Holomorphic extension theorems in Lipschitz domains of
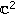 . Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0
. Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0Bory-Reyes J, Peña Peña D, Sommen F: A Davydov theorem for the isotonic Cauchy transform. Journal of Analysis and Applications 2007,5(2):109-121.
Sommen F, Peña Peña D: Martinelli-Bochner formula using Clifford analysis. Archiv der Mathematik 2007,88(4):358-363. 10.1007/s00013-006-1932-2
Brackx F, Pincket W: A Bochner-Martinelli formula for the biregular functions of Clifford analysis. Complex Variables: Theory & Application 1984,4(1):39-48.
Brackx F, Pincket W: The biregular functions of Clifford analysis: some special topics. In Clifford Algebras and Their Applications in Mathematical Physics (Canterbury, 1985), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences. Volume 183. Reidel, Dordrecht, The Netherlands; 1986:159-166.
Brackx F, Pincket W: Two Hartogs theorems for nullsolutions of overdetermined systems in Euclidean space. Complex Variables: Theory & Application 1985,4(3):205-222.
Acknowledgments
The topic covered here has been initiated while the first two authors were visiting IMPA, Rio de Janeiro, in July of 2009. Ricardo Abreu and Juan Bory wish to thank CNPq for financial support. Ricardo Abreu wishes to thank the Faculty of Ingeneering, Universidad Diego Portales, Santiago de Chile, for the kind hospitality during the period in which the final version of the paper was eventually completed. This work has been partially supported by CONICYT (Chile) under FONDECYT Grant 1090063.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abreu-Blaya, R., Bory-Reyes, J. & Bosch, P. Extension Theorem for Complex Clifford Algebras-Valued Functions on Fractal Domains. Bound Value Probl 2010, 513186 (2010). https://doi.org/10.1155/2010/513186
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/513186
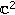 . Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0
. Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0 . to appear in Georgian Mathematical Journal
. to appear in Georgian Mathematical Journal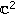 . Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0
. Advances in Applied Clifford Algebras 2010,20(1):1-12. 10.1007/s00006-008-0137-0