- Research Article
- Open access
- Published:
Accurate Asymptotic Formulas for Eigenvalues and Eigenfunctions of a Boundary-Value Problem of Fourth Order
Boundary Value Problems volume 2010, Article number: 720235 (2010)
Abstract
In the present paper, we consider a nonself-adjoint fourth-order differential operator with the periodic boundary conditions. We compute new accurate asymptotic expression of the fundamental solutions of the given equation. Then, we obtain new accurate asymptotic formulas for eigenvalues and eigenfunctions.
1. Introduction
In the present work, we consider a nonself-adjoint fourth-order operator which is generated by the periodic boundary conditions:


where  is a complex-valued function. Without lose of generality, we can assume that
is a complex-valued function. Without lose of generality, we can assume that  .
.
Spectral properties of Sturm-Liouville operator which is generated by the periodic and antiperiodic boundary conditions have been investigated by many authors, the results on this direct and references are given details in the monographs [1–5].
In this paper we obtain asymptotic formulas for the eigenvalues and eigenfunctions of the fourth-order boundary-value problem (1.1), (1.2). For second-order differential equations, similar asymptotic formulas were obtained in [6–9]. We note that in [6, 10, 11], using the obtained asymptotic formulas for eigenvalues and eigenfunctions, the basis properties of the root functions of the operators were investigated.
The paper is organized as follows. In Section 2, we compute new asymptotic expression of the fundamental solutions of (1.1). In Section 3, we obtain new accurate asymptotic estimates for the eigenvalues. In Section 4, we have asymptotic formulas for eigenfunctions under the distinct conditions on  .
.
2. The Expression of the Fundamental Solutions
It is well known that (see [2, page 92]) if the complex  -plane
-plane  is divided into eight sectors
is divided into eight sectors  , defined by the inequalities
, defined by the inequalities

then in each of these sectors (1.1) has four linear independent solutions  , which are regular with respect to
, which are regular with respect to  in the sector
in the sector  for
for  sufficiently large and which satisfy the relation
sufficiently large and which satisfy the relation

where the numbers  are the fourth roots of unity, that is,
are the fourth roots of unity, that is,  and
and  . In general, the term
. In general, the term  at the formula (2.2) depends upon the smoothness of the function
at the formula (2.2) depends upon the smoothness of the function  . If
. If has
has  continuous derivatives, then one can assert the existence of a representation (2.2) with
continuous derivatives, then one can assert the existence of a representation (2.2) with  . Here, we assume that
. Here, we assume that  . The functions
. The functions  satisfy the following recursion relations:
satisfy the following recursion relations:

Let us put, moreover,  ,
,  , for
, for  . Thus, the functions
. Thus, the functions  are uniquely determined. Thus, we can find from (2.3) that
are uniquely determined. Thus, we can find from (2.3) that

3. The Asymptotic Formulas of Eigenvalues
It follows from the classical investigations (see [4, page 65]) that the eigenvalues of the problem (1.1), (1.2) (in  ) consist of the pairs of the sequences
) consist of the pairs of the sequences  ,
,  satisfying the following asymptotic formula:
satisfying the following asymptotic formula:

for sufficiently large integer  , where
, where  is a constant.
is a constant.
Theorem 3.1.
Assume that  . Then, the eigenvalues of the boundary-value problem (1.1), (1.2) form two infinite sequences
. Then, the eigenvalues of the boundary-value problem (1.1), (1.2) form two infinite sequences  ,
,  , where
, where  is a big positive integer and have the following asymptotic formulas:
is a big positive integer and have the following asymptotic formulas:

Proof.
By derivation of (2.2) up to third order with respect to  , the following relations are obtained:
, the following relations are obtained:

where  ,
,  and
and

Now let us substitute all these expressions into the characteristic determinant

where

By long computations, for sufficiently large  , we obtain that
, we obtain that

Multiplying the last equation by

it becomes

Hence, by  , for sufficiently large
, for sufficiently large  , the following equations hold:
, the following equations hold:


By Rouche's theorem, we have asymptotic estimates for the roots  and
and  ,
,  ,
,  , of (3.10) and (3.11), respectively, where
, of (3.10) and (3.11), respectively, where  is a big positive integer
is a big positive integer


From the relations (3.12), (3.13) and the relations  , the asymptotic formulas (3.2) are valid for
, the asymptotic formulas (3.2) are valid for  .
.
4. The Asymptotic Formulas for the Eigenfunctions
Now, we obtain asymptotic formulas for eigenfunctions under the distinct conditions on  .
.
Case 1.
Assume that  and the condition
and the condition  holds. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order
holds. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order  , the following result is valid.
, the following result is valid.
Theorem 4.1.
If the condition  holds, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues
holds, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues  and
and  are of the form
are of the form


where  is sufficiently large integer.
is sufficiently large integer.
Proof.
Let us calculate  up to order
up to order  . Since
. Since

we obtain that

Follows from the condition  that
that  for
for  . Thus, we can seek eigenfunction
. Thus, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then,

By simple computations, we obtain

Hence, using the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Using the relations (3.3) and (3.12), for sufficiently large integer  , we obtain (4.1)
, we obtain (4.1)

Similarly, since  for
for  , we can seek eigenfunction
, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then,

By similar computations we obtain

Hence, using the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Hence, for sufficiently large integer  , we obtain (4.2)
, we obtain (4.2)

Case 2.
Assume that  and the conditions
and the conditions  and
and  hold. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order
hold. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order  , the following result is valid.
, the following result is valid.
Theorem 4.2.
If the conditions  and
and  hold, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues
hold, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues  and
and  are of the form
are of the form


where  is sufficiently large integer.
is sufficiently large integer.
Proof.
It is clear that

It follows from the conditions  ,
,  that
that  for
for  . Thus, we can seek eigenfunction
. Thus, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then,

By simple computations, we have

Hence, using the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Using the relations (3.3) and (3.12), for sufficiently large integer  , we obtain (4.17):
, we obtain (4.17):

In similar way, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then,

By simple computations, we get

Hence, using the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Hence, for sufficiently large integer  , we obtain (4.18):
, we obtain (4.18):

Case 3.
Assume that  and the conditions
and the conditions  and
and  hold. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order
hold. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order  , the following result is valid.
, the following result is valid.
Theorem 4.3.
If the conditions  and
and  hold, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues
hold, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues  and
and  are of the form
are of the form


where  is sufficiently large integer.
is sufficiently large integer.
Proof.
It is clear that

From the conditions  and
and  , we have
, we have 
 for
for  . Thus, we can seek eigenfunction
. Thus, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then,

By simple calculations, we get

Hence, using the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Using the relations (3.3) and (3.12), for sufficiently large integer  , we obtain (4.32)
, we obtain (4.32)

In similar way, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then,

By simple computations, we get

By the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Hence, for sufficiently large integer  , we obtain the relation (4.33)
, we obtain the relation (4.33)

Case 4.
Assume that  and the conditions
and the conditions  ,
,  and
and  hold. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order
hold. Based on the asymptotic expressions of the fundamental solutions of (1.1) and the asymptotic formulas for eigenvalues of the boundary-value problem (1.1), (1.2) up to order  , the following result is valid.
, the following result is valid.
Theorem 4.4.
If the conditions  and
and  hold, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues
hold, then eigenfunctions of the boundary-value problem (1.1), (1.2) corresponding the eigenvalues  and
and  are of the form
are of the form


where  is sufficiently large integer.
is sufficiently large integer.
Proof.
It is clear that

From the conditions  and
and  , we have
, we have  for
for  . Thus, we can seek eigenfunction
. Thus, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

Then

By simple computations, we get

By the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Using the relations (3.3) and (3.12), for sufficiently large integer  , we obtain (4.47):
, we obtain (4.47):

In similar way, we can seek eigenfunction  corresponding
corresponding  in the form
in the form

By simple computations, we get

By the formula (2.2), we can write

Therefore, for the normalized eigenfunction, we get

Hence, for sufficiently large integer  , we obtain the relation (4.48)
, we obtain the relation (4.48)

References
Dunford N, Schwartz JT: Linear Operators, Part 3 Spectral Operators, Wiley Classics Library. John Wiley & Sons, New York, NY, USA; 1970.
Levitan BM, Sargsjan IS: Introduction to Spectral Theory: Selfadjoint Ordinary Differential Operators. American Mathematical Society, Providence, RI, USA; 1975:xi+525.
Marchenko VA: Sturm-Liouville Operators and Applications, Operator Theory: Advances and Applications. Volume 22. Birkhäuser, Basel, Switzerland; 1986:xii+367.
Naimark MA: Linear Differential Operators. Part 1. Frederick Ungar, New York, NY, USA; 1967:xiii+144.
Rofe-Beketov FS, Kholkin AM: Spectral Analysis of Differential Operators, World Scientific Monograph Series in Mathematics. Volume 7. World Scientific Publishing, Singapore; 2005:xxiv+438.
Kerimov NB, Mamedov KR: On the Riesz basis property of root functions of some regular boundary value problems. Mathematical Notes 1998,64(4):483-487. 10.1007/BF02314629
Chernyatin VA: Higher-order spectral asymptotics for the Sturm-Liouville operator. Ordinary Differential Equations 2002,38(2):217-227.
Mamedov KR, Menken H:On the basisness in
 of the root functions in not strongly regular boundary value problems. European Journal of Pure and Applied Mathematics 2008,1(2):51-60.
of the root functions in not strongly regular boundary value problems. European Journal of Pure and Applied Mathematics 2008,1(2):51-60.Mamedov KR, Menken H: Asymptotic formulas for eigenvalues and eigenfunctions of a nonselfadjoint Sturm-Liouville operator. In Further Progress in Analysis. Edited by: Begehr HGW, Çelebi AO, Gilbert RP. World Scientific Publishing; 2009:798-805.
Kurbanov VM: A theorem on equivalent bases for a differential operator. Doklady Akademii Nauk 2006,406(1):17-20.
Menken H, Mamedov KR:Basis property in
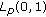 of the root functions corresponding to a boundary-value problem. Journal of Applied Functional Analysis 2010,5(4):351-356.
of the root functions corresponding to a boundary-value problem. Journal of Applied Functional Analysis 2010,5(4):351-356.
Acknowledgments
This work is supported by The Scientific and Technological Research Council of Turkey (TÜBİTAK). The author would like to thank the referee and the editor for their helpful comments and suggestions. The author also would like to thank prof. Kh. R. Mamedov for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Menken, H. Accurate Asymptotic Formulas for Eigenvalues and Eigenfunctions of a Boundary-Value Problem of Fourth Order. Bound Value Probl 2010, 720235 (2010). https://doi.org/10.1155/2010/720235
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/720235
 of the root functions in not strongly regular boundary value problems. European Journal of Pure and Applied Mathematics 2008,1(2):51-60.
of the root functions in not strongly regular boundary value problems. European Journal of Pure and Applied Mathematics 2008,1(2):51-60.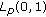 of the root functions corresponding to a boundary-value problem. Journal of Applied Functional Analysis 2010,5(4):351-356.
of the root functions corresponding to a boundary-value problem. Journal of Applied Functional Analysis 2010,5(4):351-356.