- Research
- Open access
- Published:
On a difference scheme of the second order of accuracy for elliptic-parabolic equations
Boundary Value Problems volume 2012, Article number: 80 (2012)
Abstract
The second order of accuracy difference scheme generated by Crank-Nicholson difference scheme for approximately solving multipoint nonlocal boundary value problem is considered. Well-posedness of this difference scheme in Hölder spaces is established. Furthermore, as applications, coercivity estimates in Hölder norms for approximate solutions of the multipoint nonlocal boundary value problems for mixed type equations are obtained. Moreover, the method is illustrated by numerical examples.
1 Introduction
In recent years, more and more mathematicians have been studying nonlocal problems for ordinary differential equations and partial differential equations because of their existence in many applied problems included in applied sciences. Theory and numerical methods of solutions of the nonlocal boundary value problems for these partial differential equations were investigated by many researchers (see, e.g., [1–13] and the references therein). Several types of problems in fluid mechanics, other areas of physics, and mathematical biology led to partial differential equations of elliptic-parabolic type (see, [14–18]). The purpose of this paper is to study the second order of accuracy difference schemes of elliptic-parabolic problem with nonlocal boundary value problems.
In [19], we established the well-posedness of multipoint nonlocal boundary value problem
in a Hilbert space H with the self-adjoint positive definite operator A under assumption
The well-posedness of multipoint nonlocal boundary value problem (1) in Hölder spaces with a weight was established. In applications, coercivity inequalities for the solutions of nonlocal boundary value problems for elliptic-parabolic equations were obtained.
In [20], we studied the well-posedness of the first order of accuracy difference scheme for the approximate solution of boundary value problem (1) under assumption (2).
In the present paper, we consider the second order of accuracy difference scheme generated by Crank-Nicholson difference scheme
for the approximate solution of boundary value problem (1) under assumption (2).
The well-posedness of difference scheme (3) in Hölder spaces is established. In applications, the stability, almost coercivity stability, coercivity stability estimates for solutions of the second order of accuracy difference scheme for elliptic-parabolic equations are obtained. Furthermore, the theoretical statements for the solution of the first and second order of accuracy schemes for one-dimensional elliptic-parabolic differential equation are supported by the results of a numerical example.
2 Main theorems
Let us give some auxiliary lemmas we need below. Throughout the paper, H is a Hilbert space and we denote , where A is a self-adjoint positive definite operator. Then, it is clear that B is a self-adjoint positive definite operator and , where , and which is defined on the whole space H is a bounded operator. The following operators
and

exist and are bounded for a self-adjoint positive operator A. Here,
and I is the identity operator.
Lemma 2.1 For any, and, , the solution of problem (3) exists and the following formulas hold:



Proof Clearly, the solution formula of the problem
is [22]:
for any and γ. Equation (9) and the fact that yield Equation (6).
The solution of the problem
satisfies the following formula [21]:
Equation (5) follows from Equations (9) and (11), initial condition , and
Finally, let us obtain formula (7). Combining (5), (6), and the condition
we get

From Equation (4), it follows that
This finishes the proof of Lemma 2.1. □
Here, we study well-posedness of problem (3). First, we give some necessary estimates for , and .
Lemma 2.2 For a self-adjoint positive operator A the following estimates are satisfied[21, 22, 24]:
whereis independent of τ.
From these estimates, it follows that

Now, we study well-posedness of problem (3). Let be the linear space of mesh functions defined on with values in the Hilbert space H. Next, on we denote , , , , , and , Banach spaces with the norms
Theorem 2.1 Nonlocal boundary value problem (3) is stable innorm.
Proof By [21], we have
for the solution of boundary value problem (10).
By [22], we have
for the solution of inverse Cauchy difference problem (8).
Then, the proof of Theorem 2.1 is based on stability inequalities (14), (15), and on estimates


for the solution of boundary value problem (3). Estimates (16) and (17) follow from formula (7) and estimates (12), (13). Theorem 2.1 is proved. □
Theorem 2.2 Assume thatand. Then, for the solution of difference problem (3), we have the following almost coercivity inequality:
whereis independent not only of, , φ but also of τ.
Proof By [24], we have

for the solution of inverse Cauchy difference problem (8).
By [21], we have

for the solution of boundary value problem (10). Then, the proof of Theorem 2.2 is based on almost coercivity inequalities (18), (19), and on the estimates
for the solution of boundary value problem (3). The proof of these estimates follows the scheme of papers [21, 24] and relies on both formula (7) and estimates (12), (13). This finalizes the proof of Theorem 2.2. □
Theorem 2.3 Let the assumptions of Theorem 2.2 be satisfied. Then, boundary value problem (3) is well-posed in Hölder spaces, and the following coercivity inequalities hold:
where M is independent of, , φ, τ and α.
Proof By [24],


for the solution of inverse Cauchy difference problem (8).
By [21], we have

for the solution of boundary value problem (10). Then, the proof of Theorem 2.3 is based on coercivity inequalities (20)-(22) and estimates

for the solution of difference scheme (3). The proof of these estimates follows the scheme of the papers [21, 24] and relies on both formula (7) and estimates (12), (13). This is the end of the proof of Theorem 2.3. □
3 Application
Now, the application of the abstract result is considered. In , let us consider the boundary value problem for multi-dimensional elliptic-parabolic equation
where (), (, ), (, ), and (, ) are given smooth functions. Here, Ω is the unit open cube in the n-dimensional Euclidean space (, ) with boundary S, , and .
The discretization of problem (23) is carried out in two steps. In the first step, the grid sets

are defined. To the differential operator A generated by problem (23), we assign the difference operator by formula
acting in the space of grid functions , satisfying the conditions for all . With the help of , we arrive at the nonlocal boundary value problem
for an infinite system of ordinary differential equations (see [21]).
Secondly, problem (25) is replaced by difference scheme (3), so that the following second order of accuracy difference scheme
To formulate the results, we introduce the spaces , , and of the grid functions defined on , equipped with the norms
and
Theorem 3.1 Let τ andbe sufficiently small positive numbers. Then, solutions of difference scheme (26) satisfy the following stability and almost coercivity estimates:

where M is independent not only of τ, h, but also of, and, .
The proof of Theorem 3.1 is based on Theorem 2.1, Theorem 2.2, the symmetry properties of the difference operator defined by formula (24) in , the estimate
and the following theorem in :
Theorem 3.2 For the solution of the elliptic difference problem
the following coercivity inequality holds[23]:
Here M is independent of h and.
Theorem 3.3 Let τ andbe sufficiently small positive numbers. Then, the solutions of difference scheme (26) satisfy the following coercivity stability estimates:
Here, M is independent not only of τ, h, but also of, and, .
The proof of Theorem 3.3 is based on the abstract Theorem 2.3, Theorem 3.2, and the symmetry properties of the difference operator defined by formula (24).
4 Numerical Analysis
The theoretical statements for the solution of these difference schemes are supported by the results of numerical experiments of the nonlocal boundary value problem
for the elliptic-parabolic equation. The exact solution of this problem is
For the comparison, the errors computed by the following formula
are recorded for different values of N and M, where represents the exact solution and represents the numerical solution at . The results are shown in Table 1 for respectively.
Therefore, the results indicate that the second order of accuracy difference scheme is more accurate than the first order of accuracy difference scheme.
References
Salakhitdinov MS: Equations of Mixed-Composite Type. FAN, Tashkent; 1974.
Chipot M, Lovat B: Existence and uniqueness results for a class of nonlocal elliptic and parabolic problems. Dyn. Contin. Discrete Impuls. Syst. 2001, 8(1):35-51.
Gulin AV, Ionkin NI, Morozova VA: Stability of a nonlocal two-dimensional finite-difference problem. Differ. Equ. 2001, 37(7):970-978. 10.1023/A:1011961822115
Agarwal RP, Bohner M, Shakhmurov VB: Maximal regular boundary value problems in Banach-valued weighted space. Bound. Value Probl. 2005, 1: 9-42.
Gordeziani DG, Avalishvili GA: Time-nonlocal problems for Schrödinger-type equations: I. Problems in abstract spaces. Differ. Equ. 2005, 41(5):703-711. 10.1007/s10625-005-0205-3
Gordeziani N, Natalini P, Ricci PE: Finite-difference methods for solution of nonlocal boundary value problems. Comput. Math. Appl. 2005, 50: 1333-1344. 10.1016/j.camwa.2005.05.005
Berdyshev AS, Karimov ET: Some nonlocal problems for the parabolic-hyperbolic type equation with non-characteristic line of changing type. Cent. Eur. J. Math. 2006, 4(2):183-193. 10.2478/s11533-006-0007-8
Martín-Vaquero J, Vigo-Aguiar J: On the numerical solution of the heat conduction equations subject to nonlocal conditions. Appl. Numer. Math. 2009, 59: 2507-2514. 10.1016/j.apnum.2009.05.007
Ashyralyev A, Gercek O: Finite difference method for multipoint nonlocal elliptic-parabolic problems. Comput. Math. Appl. 2010, 2010(7):2043-2052.
Gordeziani DG, Berikelashvili GK: On a nonlocal generalization of the biharmonic Dirichlet problem. Differ. Equ. 2010, 46(3):321-328. 10.1134/S001226611003002X
Gavrilyuk IP, Makarov VL, Sytnyk DO, Vasylyk VB: Exponentially convergent method for the m -point nonlocal problem for a first order differential equation in Banach space. Numer. Funct. Anal. Optim. 2011, 31(1):1-21.
Jangveladze TA, Lobjanidze GB: On a nonlocal boundary value problem for a fourth-order ordinary differential equation. Differ. Equ. 2011, 47(2):335-343.
Martín-Vaquero J, Queiruga-Dios A, Encinas AH: Numerical algorithms for diffusion-reaction problems with non-classical conditions. Appl. Math. Comput. 2012, 218(9):5487-5495. 10.1016/j.amc.2011.11.037
Vragov VN: Boundary Value Problems for Nonclassical Equations of Mathematical Physics. Textbook for Universities. NSU Publishing house, Novosibirsk; 1983.
Kröner D, Rodrigues JF: Global behaviour for bounded solutions of a porous media equation of elliptic-parabolic type. J. Math. Pures Appl. 1985, 64(2):105-120.
Nakhushev AM: Equations of Mathematical Biology. Textbook for Universities. Vysshaya Shkola, Moskow; 1995.
Ashyralyev, A, Soltanov, H: On one difference schemes for an abstract nonlocal problem generated by the investigation of the motion of gas on the homogeneous space. In: Modeling Processes of Exploitation of Gas Places and Applied Problems of Theoretical Gasohydrodynamics, pp. 147-154. Ashgabat (1998)
Diaz JI, Lerena MB, Padial JF, Rakotoson JM: An elliptic-parabolic equation with a nonlocal term for the transient regime of a plasma in a stellarator. J. Differ. Equ. 2004, 198(2):321-355. 10.1016/j.jde.2003.07.015
Gercek, O: Difference schemes of nonlocal boundary value problems for elliptic-parabolic differential equations. PhD thesis, Yildiz Teknik University (2010)
Ashyralyev A, Gercek O: On multipoint nonlocal elliptic-parabolic difference problems. Vestn. Odessa Nat. Univ. Math. Mech. 2010, 15(19):135-156.
Sobolevskii PE: The coercive solvability of difference equations. Dokl. Akad. Nauk SSSR 1971, 201(5):1063-1066.
Sobolevskii PE: On the stability and convergence of the Crank-Nicolson scheme. In Variational-Difference Methods in Mathematical Physics. Vychisl. Tsentr Sibirsk. Otdel. Akad. Nauk SSSR, Novosibirsk; 1974:146-151.
Sobolevskii PE: Difference Methods for the Approximate Solution of Differential Equations. Voronezh State University Press, Voronezh; 1975.
Ashyralyev, A, Sobolevskii, PE: Coercive stability of a Crank-Nicolson difference scheme in
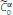 spaces. In: Approximate Methods for Investigations of Differential Equations and Their Applications, pp. 16-24. Kuybishev (1982)
spaces. In: Approximate Methods for Investigations of Differential Equations and Their Applications, pp. 16-24. Kuybishev (1982)
Acknowledgement
The authors are very grateful to Prof. P. E. Sobolevskii (Jerusalem, Israel) for valuable comments to the improvement of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The manuscript was drafted by OG and it is based on his PhD thesis. AA is the supervisor of the thesis and gave detailed comments on the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gercek, O., Ashyralyev, A. On a difference scheme of the second order of accuracy for elliptic-parabolic equations. Bound Value Probl 2012, 80 (2012). https://doi.org/10.1186/1687-2770-2012-80
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-80
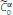 spaces. In: Approximate Methods for Investigations of Differential Equations and Their Applications, pp. 16-24. Kuybishev (1982)
spaces. In: Approximate Methods for Investigations of Differential Equations and Their Applications, pp. 16-24. Kuybishev (1982)