Skip to main content
Boundary Value Problems
Download PDF

Constant Sign and Nodal Solutions for Problems with the 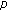-Laplacian and a Nonsmooth Potential Using Variational Techniques

Boundary Value Problems volume 2009, Article number: 820237 (2009) Cite this article

Abstract

We consider a nonlinear elliptic equation driven by the -Laplacian with a nonsmooth potential (hemivariational inequality) and Dirichlet boundary condition. Using a variational approach based on nonsmooth critical point theory together with the method of upper and lower solutions, we prove the existence of at least three nontrivial smooth solutions: one positive, the second negative, and the third sign changing (nodal solution). Our hypotheses on the nonsmooth potential incorporate in our framework of analysis the so-called asymptotically -linear problems.

Publisher note

To access the full article, please see PDF.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Florida Institute of Technology, Melbourne, FL, 32901-6975, USA

    Ravi P Agarwal

  2. Department of Mathematics, Hellenic Army Academy, Vari, 16673, Athens, Greece

    Michael E Filippakis

  3. Department of Mathematics, National University of Ireland, Galway, Ireland

    Donal O'Regan

  4. Department of Mathematics, National Technical University, Zografou Campus, 15780, Athens, Greece

    Nikolaos S Papageorgiou

Authors
  1. Ravi P Agarwal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael E Filippakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Donal O'Regan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Nikolaos S Papageorgiou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ravi P Agarwal.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and Permissions

About this article

Cite this article

Agarwal, R.P., Filippakis, M.E., O'Regan, D. et al. Constant Sign and Nodal Solutions for Problems with the 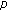-Laplacian and a Nonsmooth Potential Using Variational Techniques. Bound Value Probl 2009, 820237 (2009). https://doi.org/10.1155/2009/820237

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2009/820237

Keywords

  • Differential Equation
  • Partial Differential Equation
  • Ordinary Differential Equation
  • Functional Equation
  • Full Article