Skip to main content
Boundary Value Problems
Download PDF
  • Research Article
  • Open access
  • Published:

Topological Optimization with the 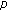-Laplacian Operator and an Application in Image Processing

Boundary Value Problems volume 2009, Article number: 896813 (2009) Cite this article

Abstract

We focus in this paper on the theoretical and numerical aspect os image processing. We consider a non linear boundary value problem (the -Laplacian) from which we will derive the asymptotic expansion of the Mumford-Shah functional. We give a theoretical expression of the topological gradient as well as a numerical confirmation of the result in the restoration and segmentation of images.

Publisher note

To access the full article, please see PDF.

Author information

Authors and Affiliations

  1. Université de Bambey, Bambey, Senegal

    Alassane Sy

  2. Laboratoire de Mathématique de la Décision et d'Analyse Numérique (LMDAN), Ecole Doctorale de Mathématiques et Informatique, Université Cheikh Anta Diop de Dakar, B.p. 16 889, Dakar-Fann, Senegal

    Diaraf Seck

Authors
  1. Alassane Sy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Diaraf Seck
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Diaraf Seck.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Sy, A., Seck, D. Topological Optimization with the 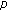-Laplacian Operator and an Application in Image Processing. Bound Value Probl 2009, 896813 (2009). https://doi.org/10.1155/2009/896813

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2009/896813

Keywords