- Research Article
- Open access
- Published:
Multiple Solutions of 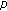 -Laplacian with Neumann and Robin Boundary Conditions for Both Resonance and Oscillation Problem
-Laplacian with Neumann and Robin Boundary Conditions for Both Resonance and Oscillation Problem
Boundary Value Problems volume 2011, Article number: 214289 (2011)
Abstract
We discuss Neumann and Robin problems driven by the  -Laplacian with jumping nonlinearities. Using sub-sup solution method, Fucík spectrum, mountain pass theorem, degree theorem together with suitable truncation techniques, we show that the Neumann problem has infinitely many nonconstant solutions and the Robin problem has at least four nontrivial solutions. Furthermore, we study oscillating equations with Robin boundary and obtain infinitely many nontrivial solutions.
-Laplacian with jumping nonlinearities. Using sub-sup solution method, Fucík spectrum, mountain pass theorem, degree theorem together with suitable truncation techniques, we show that the Neumann problem has infinitely many nonconstant solutions and the Robin problem has at least four nontrivial solutions. Furthermore, we study oscillating equations with Robin boundary and obtain infinitely many nontrivial solutions.
Publisher note
To access the full article, please see PDF.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, J., Xue, X. Multiple Solutions of 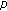 -Laplacian with Neumann and Robin Boundary Conditions for Both Resonance and Oscillation Problem.
Bound Value Probl 2011, 214289 (2011). https://doi.org/10.1155/2011/214289
-Laplacian with Neumann and Robin Boundary Conditions for Both Resonance and Oscillation Problem.
Bound Value Probl 2011, 214289 (2011). https://doi.org/10.1155/2011/214289
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/214289