- Research Article
- Open access
- Published:
Nodal Solutions for a Class of Fourth-Order Two-Point Boundary Value Problems
Boundary Value Problems volume 2010, Article number: 570932 (2010)
Abstract
We consider the fourth-order two-point boundary value problem  ,
,  ,
,  , where
, where  is a parameter,
is a parameter,  is given constant,
is given constant,  with
with  on any subinterval of
on any subinterval of  ,
,  satisfies
satisfies  for all
for all  , and
, and  ,
,  ,
,  for some
for some  . By using disconjugate operator theory and bifurcation techniques, we establish existence and multiplicity results of nodal solutions for the above problem.
. By using disconjugate operator theory and bifurcation techniques, we establish existence and multiplicity results of nodal solutions for the above problem.
1. Introduction
The deformations of an elastic beam in equilibrium state with fixed both endpoints can be described by the fourth-order ordinary differential equation boundary value problem

where  is continuous,
is continuous,  is a parameter. Since the problem (1.1) cannot transform into a system of second-order equation, the treatment method of second-order system does not apply to the problem (1.1). Thus, existing literature on the problem (1.1) is limited. In 1984, Agarwal and chow [1] firstly investigated the existence of the solutions of the problem (1.1) by contraction mapping and iterative methods, subsequently, Ma and Wu [2] and Yao [3, 4] studied the existence of positive solutions of this problem by the Krasnosel'skii fixed point theorem on cones and Leray-Schauder fixed point theorem. Especially, when
is a parameter. Since the problem (1.1) cannot transform into a system of second-order equation, the treatment method of second-order system does not apply to the problem (1.1). Thus, existing literature on the problem (1.1) is limited. In 1984, Agarwal and chow [1] firstly investigated the existence of the solutions of the problem (1.1) by contraction mapping and iterative methods, subsequently, Ma and Wu [2] and Yao [3, 4] studied the existence of positive solutions of this problem by the Krasnosel'skii fixed point theorem on cones and Leray-Schauder fixed point theorem. Especially, when  , Korman [5] investigated the uniqueness of positive solutions of the problem (1.1) by techniques of bifurcation theory. However, the existence of sign-changing solution for this problem have not been discussed.
, Korman [5] investigated the uniqueness of positive solutions of the problem (1.1) by techniques of bifurcation theory. However, the existence of sign-changing solution for this problem have not been discussed.
In this paper, applying disconjugate operator theory and bifurcation techniques, we consider the existence of nodal solution of more general the problem:

under the assumptions:
(H1)  is a parameter,
is a parameter,  is given constant,
is given constant,
(H2)  with
with  on any subinterval of
on any subinterval of  ,
,
(H3)  satisfies
satisfies  for all
for all  , and
, and

for some  .
.
However, in order to use bifurcation technique to study the nodal solutions of the problem (1.2), we firstly need to prove that the generalized eigenvalue problem

(where  satisfies (H2)) has an infinite number of positive eigenvalues
satisfies (H2)) has an infinite number of positive eigenvalues

and each eigenvalue corresponding an essential unique eigenfunction  which has exactly
which has exactly  simple zeros in
simple zeros in  and is positive near 0. Fortunately, Elias [6] developed a theory on the eigenvalue problem
and is positive near 0. Fortunately, Elias [6] developed a theory on the eigenvalue problem

where

and  with
with  on
on  .
.  are called the quasi-derivatives of
are called the quasi-derivatives of  . To apply Elias's theory, we have to prove that (1.4) can be rewritten to the form of (1.6), that is, the linear operator
. To apply Elias's theory, we have to prove that (1.4) can be rewritten to the form of (1.6), that is, the linear operator

has a factorization of the form

on  , where
, where  with
with  on
on  , and
, and  if and only if
if and only if

This can be achieved under (H1) by using disconjugacy theory in [7].
The rest of paper is arranged as follows: in Section 2, we state some disconjugacy theory which can be used in this paper, and then show that (H1) implies the equation

is disconjugacy on  , moreover, we establish some preliminary properties on the eigenvalues and eigenfunctions of the generalized eigenvalue problem (1.4). Finally in Section 3, we state and prove our main result.
, moreover, we establish some preliminary properties on the eigenvalues and eigenfunctions of the generalized eigenvalue problem (1.4). Finally in Section 3, we state and prove our main result.
Remark 1.1.
For other results on the existence and multiplicity of positive solutions and nodal solutions for boundary value problems of ordinary differential equations based on bifurcation techniques, see Ma [8–12], An and Ma [13], Yang [14] and their references.
2. Preliminary Results
Let

be  th-order linear differential equation whose coefficients
th-order linear differential equation whose coefficients  are continuous on an interval
are continuous on an interval  .
.
Definition 2.1 (see [7, Definition  , page 2]).
, page 2]).
Equation (2.1) is said to be disconjugate on an interval  if no nontrivial solution has
if no nontrivial solution has  zeros on
zeros on  , multiple zeros being counted according to their multiplicity.
, multiple zeros being counted according to their multiplicity.
Lemma 2.2 (see [7, Theorem  , page 3]).
, page 3]).
Equation (2.1) is disconjugate on a compact interval  if and only if there exists a basis of solutions
if and only if there exists a basis of solutions  such that
such that

on  . A disconjugate operator
. A disconjugate operator  can be written as
can be written as

where  and
and

and 
Lemma 2.3 (see [7, Theorem  , page 9]).
, page 9]).
Green's function  of the disconjugate Equation (2.3) and the two-point boundary value conditions
of the disconjugate Equation (2.3) and the two-point boundary value conditions

satisfies

Now using Lemmas 2.2 and 2.3, we will prove some preliminary results.
Theorem 2.4.
Let (H1) hold. Then
(i)  is disconjugate on
is disconjugate on  , and
, and  has a factorization
has a factorization

where  with
with 
(ii)  if and only if
if and only if

where

Proof.
We divide the proof into three cases.
Case 1.
 . The case is obvious.
. The case is obvious.
Case 2.
 .
.
In the case, take

where  ,
,  is a positive constant. Clearly,
is a positive constant. Clearly,  and then
and then

It is easy to check that  ,
, ,
, ,
, form a basis of solutions of
form a basis of solutions of  . By simple computation, we have
. By simple computation, we have

Clearly,  on
on 
By Lemma 2.2,  is disconjugate on
is disconjugate on  , and
, and  has a factorization
has a factorization

and accordingly

Using (2.14), we conclude that  is equivalent to (2.8).
is equivalent to (2.8).
Case 3.
 .
.
In the case, take

where  .
.
It is easy to check that  ,
,  ,
,  ,
,  form a basis of solutions of
form a basis of solutions of  . By simple computation, we have
. By simple computation, we have

From  and
and  , we have
, we have  , so
, so  on
on 
By Lemma 2.2,  is disconjugate on
is disconjugate on  , and
, and  has a factorization
has a factorization

and accordingly

Using (2.18), we conclude that  is equivalent to (2.8).
is equivalent to (2.8).
This completes the proof of the theorem.
Theorem 2.5.
Let (H1) hold and  satisfy (H2). Then
satisfy (H2). Then
(i) Equation (1.4) has an infinite number of positive eigenvalues

(ii)  as
as 
(iii) To each eigenvalue there corresponding an essential unique eigenfunction  which has exactly
which has exactly  simple zeros in
simple zeros in  and is positive near 0.
and is positive near 0.
(iv) Given an arbitrary subinterval of  , then an eigenfunction which belongs to a sufficiently large eigenvalue change its sign in that subinterval.
, then an eigenfunction which belongs to a sufficiently large eigenvalue change its sign in that subinterval.
(v) For each  , the algebraic multiplicity of
, the algebraic multiplicity of  is 1.
is 1.
Proof.
(i)–(iv) are immediate consequences of Elias [6, Theorems  ] and Theorem 2.4. we only prove (v).
] and Theorem 2.4. we only prove (v).
Let

with

To show (v), it is enough to prove

Clearly

Suppose on the contrary that the algebraic multiplicity of  is greater than 1. Then there exists
is greater than 1. Then there exists  , and subsequently
, and subsequently

for some  . Multiplying both sides of (2.24) by
. Multiplying both sides of (2.24) by  and integrating from 0 to 1, we deduce that
and integrating from 0 to 1, we deduce that

which is a contradiction!
Theorem 2.6 (Maximum principle).
Let (H1) hold. Let  with
with  on
on  and
and  in
in  . If
. If  satisfies
satisfies

Then  on
on  .
.
Proof.
When  , the homogeneous problem
, the homogeneous problem

has only trivial solution. So the boundary value problem (2.26) has a unique solution which may be represented in the form

where  is Green's function.
is Green's function.
By Theorem 2.4 and Lemma 2.3 (take  ), we have
), we have

that is, 
Using (2.28), when  on
on  with
with  in
in  , then
, then  on
on  .
.
3. Statement of the Results
Theorem 3.1.
Let (H1), (H2), and (H3) hold. Assume that for some  ,
,

Then there are at least  nontrivial solutions of the problem (1.2). In fact, there exist solutions
nontrivial solutions of the problem (1.2). In fact, there exist solutions  such that for
such that for  ,
,  has exactly
has exactly  simple zeros on the open interval
simple zeros on the open interval  and
and  and there exist solutions
and there exist solutions  such that for
such that for  ,
,  has exactly
has exactly  simple zeros on the open interval
simple zeros on the open interval  and
and  .
.
Let  with the norm
with the norm  Let
Let

with the norm  Then
Then  is completely continuous, here
is completely continuous, here  is given as in (2.20).
is given as in (2.20).
Let  be such that
be such that

here  . Clearly
. Clearly

Let

then  is nondecreasing and
is nondecreasing and

Let us consider

as a bifurcation problem from the trivial solution  .
.
Equation (3.7) can be converted to the equivalent equation

Further we note that  for
for  near 0 in
near 0 in  .
.
In what follows, we use the terminology of Rabinowitz [15].
Let  under the product topology. Let
under the product topology. Let  denote the set of function in
denote the set of function in  which have exactly
which have exactly  interior nodal (i.e., nondegenerate) zeros in
interior nodal (i.e., nondegenerate) zeros in  and are positive near
and are positive near  , set
, set  , and
, and  . They are disjoint and open in
. They are disjoint and open in  . Finally, let
. Finally, let  and
and  .
.
The results of Rabinowitz [13] for (3.8) can be stated as follows: for each integer  ,
,  , there exists a continuum
, there exists a continuum  of solutions of (3.8), joining
of solutions of (3.8), joining  to infinity in
to infinity in  . Moreover,
. Moreover,  .
.
Notice that we have used the fact that if  is a nontrivial solution of (3.7), then all zeros of
is a nontrivial solution of (3.7), then all zeros of  on
on  are simply under (H1), (H2), and (H3).
are simply under (H1), (H2), and (H3).
In fact, (3.7) can be rewritten to

where

clearly  satisfies (H2). So Theorem 2.5(iii) yields that all zeros of
satisfies (H2). So Theorem 2.5(iii) yields that all zeros of  on
on  are simple.
are simple.
Proof of Theorem 3.1.
We only need to show that

Suppose on the contrary that

where

Since  joins
joins  to infinity in
to infinity in  and
and  is the unique solutions of (3.7)
is the unique solutions of (3.7)  in
in  , there exists a sequence
, there exists a sequence  such that
such that  and
and  as
as  . We may assume that
. We may assume that  as
as  . Let
. Let  . From the fact
. From the fact

we have that

Furthermore, since  is completely continuous, we may assume that there exist
is completely continuous, we may assume that there exist  with
with  such that
such that  as
as  .
.
Since

we have from (3.15) and (3.6) that

that is,

By (H2), (H3), and (3.17) and the fact that  , we conclude that
, we conclude that  , and consequently
, and consequently

By Theorem 2.6, we know that  in
in  . This means
. This means  is the first eigenvalue of
is the first eigenvalue of  and
and  is the corresponding eigenfunction. Hence
is the corresponding eigenfunction. Hence  . Since
. Since  is open and
is open and  , we have that
, we have that  for
for  large. But this contradict the assumption that
large. But this contradict the assumption that  and
and  , so (3.12) is wrong, which completes the proof.
, so (3.12) is wrong, which completes the proof.
References
Agarwal RP, Chow YM: Iterative methods for a fourth order boundary value problem. Journal of Computational and Applied Mathematics 1984,10(2):203-217. 10.1016/0377-0427(84)90058-X
Ma R, Wu HP: Positive solutions of a fourth-order two-point boundary value problem. Acta Mathematica Scientia A 2002,22(2):244-249.
Yao Q: Positive solutions for eigenvalue problems of fourth-order elastic beam equations. Applied Mathematics Letters 2004,17(2):237-243. 10.1016/S0893-9659(04)90037-7
Yao Q: Solvability of an elastic beam equation with Caratheodory function. Mathematica Applicata 2004,17(3):389-392.
Korman P: Uniqueness and exact multiplicity of solutions for a class of fourth-order semilinear problems. Proceedings of the Royal Society of Edinburgh A 2004,134(1):179-190. 10.1017/S0308210500003140
Elias U:Eigenvalue problems for the equations
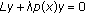 . Journal of Differential Equations 1978,29(1):28-57. 10.1016/0022-0396(78)90039-6
. Journal of Differential Equations 1978,29(1):28-57. 10.1016/0022-0396(78)90039-6Elias U: Oscillation Theory of Two-Term Differential Equations, Mathematics and Its Applications. Volume 396. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:viii+217.
Ma R: Existence of positive solutions of a fourth-order boundary value problem. Applied Mathematics and Computation 2005,168(2):1219-1231. 10.1016/j.amc.2004.10.014
Ma R: Nodal solutions for a fourth-order two-point boundary value problem. Journal of Mathematical Analysis and Applications 2006,314(1):254-265.
Ma R: Nodal solutions of boundary value problems of fourth-order ordinary differential equations. Journal of Mathematical Analysis and Applications 2006,319(2):424-434. 10.1016/j.jmaa.2005.06.045
Ma R, Xu J: Bifurcation from interval and positive solutions of a nonlinear fourth-order boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2010,72(1):113-122. 10.1016/j.na.2009.06.061
Ma R, Wang H: On the existence of positive solutions of fourth-order ordinary differential equations. Applicable Analysis 1995,59(1–4):225-231.
An Y, Ma R:Global behavior of the components for the second order
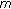 -point boundary value problems. Boundary Value Problems 2008, 2008:-10.
-point boundary value problems. Boundary Value Problems 2008, 2008:-10.Yang Z: Existence and uniqueness of positive solutions for higher order boundary value problem. Computers & Mathematics with Applications 2007,54(2):220-228. 10.1016/j.camwa.2007.01.018
Rabinowitz PH: Some global results for nonlinear eigenvalue problems. Journal of Functional Analysis 1971,7(3):487-513. 10.1016/0022-1236(71)90030-9
Acknowledgments
This work is supported by the NSFC (no. 10671158), the Spring-sun program (no. Z2004-1-62033), SRFDP (no. 20060736001), the SRF for ROCS, SEM (2006[ ]), NWNU-KJCXGC-SK0303-23, and NWNU-KJCXGC-03-69.
]), NWNU-KJCXGC-SK0303-23, and NWNU-KJCXGC-03-69.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, J., Han, X. Nodal Solutions for a Class of Fourth-Order Two-Point Boundary Value Problems. Bound Value Probl 2010, 570932 (2010). https://doi.org/10.1155/2010/570932
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/570932
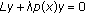 . Journal of Differential Equations 1978,29(1):28-57. 10.1016/0022-0396(78)90039-6
. Journal of Differential Equations 1978,29(1):28-57. 10.1016/0022-0396(78)90039-6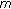 -point boundary value problems. Boundary Value Problems 2008, 2008:-10.
-point boundary value problems. Boundary Value Problems 2008, 2008:-10.