- Research
- Open access
- Published:
Riemann boundary value problem for H-2-monogenic function in Hermitian Clifford analysis
Boundary Value Problems volume 2014, Article number: 81 (2014)
Abstract
Hermitian Clifford analysis has emerged as a new and successful branch of Clifford analysis, offering yet a refinement of the Euclidean case; it focuses on the simultaneous null solutions of two Hermitian Dirac operators. Using a circulant matrix approach, we will study the Riemann type problems in Hermitian Clifford analysis. We prove a mean value formula for the Hermitian monogenic function. We obtain a Liouville-type theorem and a maximum module for the function above. Applying the Plemelj formula, integral representation formulas, and a Liouville-type theorem, we prove that the Riemann type problems for Hermitian monogenic and Hermitian-2-monogenic functions are solvable. Explicit representation formulas of the solutions are also given.
1 Introduction
The classical Riemann boundary value problem (BVP for short) theory in the complex plane has been systematically developed, see [1] and [2]. It is natural to generalize the classical Riemann BVP theory to higher dimensions. Euclidean Clifford analysis is a higher dimensional function theory offering a refinement of classical harmonic analysis and a generation of complex in plane analysis. The theory is centered around the concept of monogenic functions, see [3–6], etc. Under the framework, in [7–12], many interesting results about BVP for monogenic functions in Clifford analysis were presented. In [13] and [14], Riemann BVP for harmonic functions (i.e., 2-monogenic functions) and biharmonic functions were studied, the solutions are given in an explicit way.
More recently, Hermitian Clifford analysis has emerged as a new and successful branch of Clifford analysis, offering yet a refinement of the Euclidean case; it focuses on the simultaneous null solutions of two Hermitian Dirac operators invariant under the action of the unitary group. This function theory can be found in [15] and [16], etc. In [17], based on the complex Clifford algebra , the Hermitian Cauchy integral formulas were constructed in the framework of circulant matrix functions, and the intimate relationship with holomorphic function theory of several complex variables was considered. For details, we refer to [17–20]. In [18] and [21], a matrix Hilbert transform in Hermitian Clifford analysis was studied, and analogs of characteristic properties of the matrix Hilbert transform in classical analysis and orthogonal Clifford analysis were given, for example by the usual Plemelj-Sokhotski formula. Under this setting it is natural to consider the Riemann BVP. In [22], the Riemann BVP for (left) Helmholtz H-monogenic functions (i.e., null solutions of perturbed Hermitian Dirac operators in the framework of Hermitian Clifford analysis). If the perturbed value vanishes, is , then the Riemann BVP for H-monogenic circulant matrix functions was solved. Also, we naturally consider Riemann BVP for H-monogenic circulant matrix functions (i.e., null solutions to ) and H-2-monogenic circulant matrix functions (i.e., null solutions to ). Roughly speaking Riemann BVP means that we prescribe that the solutions are bounded at infinity. Up to present, as far as we know, it is a new problem. In this paper, motivated by [8, 9, 13, 14, 17, 18], we will consider Riemann BVP for H-2-monogenic circulant matrix functions in Hermitian Clifford analysis. Applying the integral representation formulas of H-monogenic circulant matrix functions and H-2-monogenic circulant matrix functions, we get mean values formulas. Furthermore we prove a maximum modulus theorem and a Liouville theorem in Hermitian Clifford analysis. Finally we get explicit solutions for Riemann BVP for H-2-monogenic circulant matrix functions in Hermitian Clifford analysis. Some results of [14] and [22] are generalized in our paper.
2 Preliminaries
In this section we recall some basic facts about Clifford algebras and Hermitian Clifford analysis which will be needed in the sequel. More details can also be found in [4] and [5].
Let be an 2n-dimensional () real linear space with basis , be the -dimensional real linear space with basis
where N stands for the set and let denote the family of all order-preserving subsets of N in the above way. Now denote by and by for . The product on is defined by
where is the cardinal number of the set A, the number , , the symmetric difference set is also order-preserving in the above way, and is the coefficient of the -component of the Clifford number λ. Also, denote by . It follows at once from the multiplication rule (2.1) that is the identity element written now as 1 and, in particular,
Thus is a real linear, associative, but non-commutative algebra and it is called the Clifford algebra over . An involution is defined by
From (2.1) and (2.3), we have
The Euclidean space is embedded in by identifying with the Clifford vector given by
Note that the square of is scalar valued and equals the norm squared up to a minus sign: . The dual of is the vector-valued first order differential operator
called a Dirac operator. It is precisely this Dirac operator which underlies the notion of monogenicity of a function, a notion which is the higher dimensional counterpart of holomorphy in the complex plane. A function f defined and differentiable in an open region Ω of and taking values in is called (left) monogenic in Ω if . As the Dirac operator factorizes the Laplacian, , monogenicity can be regarded as a refinement of harmonicity. We refer to this setting as the orthogonal case, since the fundamental group leaving the Dirac operator invariant is the special orthogonal group , which is doubly covered by the group of the Clifford algebra . For this reason, the Dirac operator is also called rotation invariant. When allowing for complex constants, the set of generators produces the complex Clifford algebra , being the complexification of the real Clifford algebra , i.e. . Any complex Clifford number may be written as , , an observation leading to the definition of the Hermitian conjugation , where the bar notation stands for the usual Clifford conjugation in , i.e. the main anti-involution for which , . This Hermitian conjugation also leads to a Hermitian inner product and its associated norm on is given by and .
The above will be the framework for the so-called Hermitian Clifford analysis, yet a refinement of orthogonal Clifford analysis. An elegant way for introducing this setting consists in considering a so-called complex structure, i.e. a specific -element J for which (see [15–17]). Here, J is chosen to act upon the generators of the Clifford algebra as
With J one may associate two projection operators which will produce the main protagonists of the Hermitian setting by acting upon the corresponding objects in the orthogonal framework. First of all, the so-called Witt basis elements for the complex Clifford algebra are obtained through the action of on the orthogonal basis elements :
These Witt basis elements satisfy the Grassmann identities,
and the duality identities,
Next we identify a vector in with the Clifford vector and we denote by the action of the complex structure J on , i.e.
Note that the vectors and are orthogonal, the Clifford vectors and anti-commute. The actions of the projection operators on the Clifford vector then produce the Hermitian Clifford variables and its Hermitian conjugate :
which can be rewritten in terms of the Witt basis elements as
where n complex variables have been introduced, with complex conjugates , . Finally, the Hermitian Dirac operators and are derived from the orthogonal Dirac operator :
where we have introduced
In view of the Witt basis, the Hermitian Dirac operators are expressed as
involving the classical Cauchy-Riemann operators and their complex conjugates in the complex -planes, .
Finally observe that the Hermitian vector variables and Dirac operators are isotropic, since the Witt basis elements are, i.e.
whence the Laplacian allows for the decomposition
while also
For further use, we introduce the Hermitian oriented surface elements and as follows:
where denotes the vector-valued oriented surface element and . They are explicitly given by means of the following differential forms of order :
here
and the corresponding oriented volume elements then read
We also consider the associated volume element , defined as
reflecting integration over the respective complex -planes, . One has
We still introduce the matrix
which will play the role of the differential form.
Definition 2.1 A continuously differentiable function f on an open region Ω of with values in is called a (left) h-monogenic function in Ω, iff it satisfies in Ω the system
or, equivalently, the system
The respective fundamental solutions of and are given by
where denotes the area of the unit sphere in . The transition from Hermitian Clifford analysis to a circulant matrix approach is essentially based on the following observation. Introducing the particular circulant matrices
where and . Then , where δ is the diagonal matrix with the Dirac delta distribution δ on the diagonal, may be considered as a fundamental solution of the matrix operator . This has also led to a theory of H-monogenic circulant matrix functions, the framework for this theory being as follows. Let , be continuously differentiable functions defined in Ω and taking values in , and consider the corresponding circulant matrix function
The ring of such matrix functions over is denoted by . In what follows, O will be denoting the matrix in with zero entries.
Definition 2.2 The matrix function is called (left) H-monogenic in Ω if and only if it satisfies in Ω the system .
The notions of continuity, differentiability, and integrability of have the usual component-wise meaning. In particular, we will need to defined in this way the classes , , of r times continuously differentiable functions over some suitable subset Ω of , stands for Hölder continuous circulant matrix functions over Ω. We introduce the non-negative function
where denotes the Clifford norm.
Definition 2.3 The matrix function () is called (left) H-2-monogenic in Ω if and only if it satisfies in Ω the system .
In what follows we suppose
with .
3 Some properties for H-monogenic circulant matrix functions
Theorem 3.1 If the matrix functions is H-monogenic in Ω then
for each such that .
Proof Take such that . Apply Hermitian Cauchy’s integral formula I (in [17]). On the ball , we have
where
As , we apply the Hermitian Clifford-Stokes theorem (in [17]),
The result follows. □
The notions of continuity, differentiability, and integrability of have the usual component-wise meaning.
Theorem 3.2 (Liouville theorem)
If the matrix function is H-monogenic in and satisfies for all then must be a constant circulant matrix in .
Proof By Theorem 3.1, we have
where denotes the symmetric difference of and , is Lebesgue volume measure on , so that . The last expression above tends to 0 as . Thus and so is a constant circulant matrix. □
Theorem 3.3 (Maximum modulus theorem)
Let the matrix functions be a H-monogenic in the open and connected set Ω. If there exists a point such that
for all , then must be constant circulant matrix in Ω.
Proof Put and consider the subset of Ω given by
Since , then . So let ; this implies that . As is continuous in Ω, there exists an such that . This means that is relatively closed in Ω.
Now take and such that . By Theorem 3.1, we have
i.e.
we then have
Applying Hölder’s inequality,
Hence
which yields for all , this means that and hence that is relatively open in Ω. As Ω is supposed to be connected it follows that .
Now if then clearly for all . For , since is H-monogenic in Ω, we have
then for all , and . Hence we obtain and for all . For all we have
i.e.
and by (3.7), differentiating twice, we get
Summing up over yields
we have () in Ω for all all . Thus , are constants in Ω. The result follows. □
Corollary 3.4 Let Ω be a bounded open set in and suppose that , are functions in and is H-monogenic in Ω. Then
4 Higher order Hermitian Borel-Pompeiu formula in Hermitian Clifford analysis
Integral representation formulas in Clifford analysis have been well developed in [3, 23–25], etc. These integral representation formulas are powerful tools. In this section, we get the explicit expression of the kernel function for and then get the explicit integral representation formulas for functions in Hermitian Clifford analysis. These explicit integral representation formulas play an important role in studying the further properties of the functions in Hermitian Clifford analysis.
In what follows, we denote
where denotes the area of the unit sphere in .
Lemma 4.1 Let be as in (4.5). Then .
Proof The identity is obtained by straightforward calculation. □
Lemma 4.2 Denote , , then
-
1.
(4.6)
-
2.
(4.7)
Lemma 4.3 Let and be as in (4.4) and (4.3). Then
Proof In view of Lemma 4.2, the identity is obtained by straightforward calculation. □
Theorem 4.4 (Higher order Hermitian Borel-Pompeiu formula)
Suppose is a 2n-dimensional compact differentiable and oriented manifold with smooth boundary ∂ Γ, and are functions in and is the matrix function. It then follows that
Proof First let . It then follows from the Stokes formula, which can be found in [17], that we have
then the left-hand side of the stated formula apparently equals zero.
Now, let and take such that . Invoking the previous case, we may then write
Here we take the limits for . In view of the weak singularity of the third term of (4.11) yields
since the integrand only contains functions which are integrable on Γ. Furthermore we may write
we denote
Combining the Stokes formula in Hermitian Clifford analysis with
we get
where is defined as in (4.2).
It is clear that
Then the result follows. □
Theorem 4.5 If the matrix function is H-2-monogenic in Ω then
Proof Since is H-2-monogenic in Ω, in view of Theorem 4.4, the result follows. □
Theorem 4.6 Let be an open ball centered at with radius R in , and the matrix function is H-2-monogenic in , then for all
Theorem 4.7 (Mean value theorem for H-2-monogenic matrix function)
If the matrix function is H-2-monogenic in Ω then
for each such that .
Proof Take such that , by Theorem 4.5 we get
Combining with the Stokes formula in Hermitian Clifford analysis, is H-2-monogenic in Ω, Lemma 4.3 with , we have
The proof is done. □
Corollary 4.8 If the matrix function is H-2-monogenic in and satisfies for all , then must be a constant circulant matrix in .
Proof The proof is similar to the method in Theorem 3.2. □
Suppose Ω is an open bounded non-empty subset of with a Liapunov boundary ∂ Ω, we usually write and . The notations and will be reserved for Clifford vectors associated to points , while their Hermitian counterparts are denoted and . By means of the matrix approach sketched above, the following Hermitian Plemelj-Sokhotski formula.
We shall introduce the following matrix operators:
where .
Let . Then the boundary values of the Hermitian Cauchy integral are given by
Theorem 4.10 Let be an open ball centered at , with radius R in , , in , , . Then in .
Proof We only need to prove that for any , . Define , . For any , taking constants , is a ball with the center at and radius δ such that . Obviously, is a Liapunov boundary. Using the Hermitian Borel-Pompeiu formula, we have
Using Lemma 4.9, for , we obtain
Combining (4.26) with (4.27), we get
Therefore , and the result follows. □
Theorem 4.11 Let be an open ball centered at , with radius R in , , in , and satisfies the following conditions:
where , then in .
Proof In view of the weak singularity of , combining Theorem 4.6 with Lemma 4.9, the theorem can be similarly proved similarly to Theorem 4.10. □
Theorem 4.12 Let , in ,
where , (), then for
where be a constant circulant matrix.
5 Riemann boundary value problem for H-monogenic functions
An Riemann boundary value problem for H-monogenic functions is denoted as follows:
where is any invertible constant circulant matrix, we denote by an invertible element for . Here is a given circulant matrix function in , .
Theorem 5.1 The Riemann boundary value problem (5.1) is solvable and the solution can be written as
Proof Let
Furthermore, we denote
and we then have , . The transmission condition
can be changed into
and if we denote
then , , and . Using Lemma 4.9, we have
From (5.5) and (5.7) we have
Combining Theorem 3.2 with Theorem 4.10, there exists a constant circulant matrix such that .
On the other hand, it can be directly proved that (5.2) is the solution of (5.1), and the proof is done. □
Remark 5.2 If (5.1) is solved in , i.e. is required, then the problem has the unique solution (5.2) (taking ).
6 Riemann boundary value problem for H-2-monogenic function in Hermitian Clifford analysis
In this section, we shall consider the following Riemann boundary value problem:
where , are invertible constant circulant matrices and , are given circulant matrix functions in , . We shall give the explicit expression of solutions for (6.1).
Theorem 6.1 The Riemann boundary value problem (6.1) is solvable and the solution is given by
where
Proof Let be the solution of (6.1) for . We denote . Then
By and Theorem 5.1, we have
We denote
Combining (6.6) with (6.7) we then get
If we denote , where and use
then we obtain
where is denoted as in (6.4).
It is obvious that , . Since , using Theorem 5.1 we get the following representation:
Combining (6.7) with (6.10) we arrive at the proposed result.
On the other hand, it can be directly proved that (6.2) are the solution of (6.1) and the proof is done. □
Remark 6.2 If (6.1) is solved in , i.e. is required, then the problem has the unique solution (6.2) (taking ).
References
Muskhelishvilli NI: Singular Integral Equations. Nauka, Moscow; 1968.
Lu J: Boundary Value Problems of Analytic Functions. World Scientific, Singapore; 1993.
Brackx F, Delanghe R, Sommen F Research Notes in Mathematics 76. In Clifford Analysis. Pitman, London; 1982.
Delanghe R, Sommen F, Souček V: Clifford Algebra and Spinor-Valued Functions. Kluwer Academic, Dordrecht; 1992.
Delanghe R: On the regular analytic functions with values in a Clifford algebra. Math. Ann. 1970, 185: 91-111. 10.1007/BF01359699
Delanghe R: On the singularities of functions with values in a Clifford algebra. Math. Ann. 1972, 196: 293-319. 10.1007/BF01428219
Bernstein S: On the left linear Riemann problem in Clifford analysis. Bull. Belg. Math. Soc. Simon Stevin 1996, 3: 557-576.
Zhang Z, Du J: On certain Riemann boundary value problems and singular integral equations in Clifford analysis. Chin. Ann. Math., Ser. A 2000, 22: 421-426.
Xu Z: On linear and nonlinear Riemann-Hilbert problems for regular functions with values in a Clifford algebra. Chin. Ann. Math., Ser. B 1990, 11(3):349-358.
Abreu Blaya R, Bory Reyes J: On the Riemann Hilbert type problems in Clifford analysis. Adv. Appl. Clifford Algebras 2001, 11(1):15-26. 10.1007/BF03042036
Bory Reyes J, Abreu Blaya R: The quaternionic Riemann problem with natural geometric condition on the boundary. Complex Var. Theory Appl. 2000, 42: 135-149. 10.1080/17476930008815278
Abreu Blaya R, Bory Reyes J: Boundary value problems for quaternionic monogenic functions on non-smooth surfaces. Adv. Appl. Clifford Algebras 1999, 9(1):1-22. 10.1007/BF03041934
Gürlebeck K, Zhang Z: Some Riemann boundary value problems in Clifford analysis. Math. Methods Appl. Sci. 2010, 33: 287-302.
Zhang Z, Gürlebeck K: Some Riemann boundary value problems in Clifford analysis (I). Complex Var. Elliptic Equ. 2013, 58: 991-1003. 10.1080/17476933.2011.613119
Brackx F, Bureš J, De Schepper H, Eelbode D, Sommen F, Soucěk V: Fundaments of Hermitean Clifford analysis part I: complex structure. Complex Anal. Oper. Theory 2007, 1(3):341-365. 10.1007/s11785-007-0010-5
Brackx F, Bureš J, De Schepper H, Eelbode D, Sommen F, Soucěk V: Fundamentals of Hermitean Clifford analysis part II: splitting of h -monogenic equations. Complex Var. Elliptic Equ. 2007, 52: 1068-1078.
Brackx F, De Knock B, De Schepper H, Sommen F: On Cauchy and Martinelli-Bochner integral formulae in Hermitean Clifford analysis. Bull. Braz. Math. Soc. 2009, 40(3):395-461. 10.1007/s00574-009-0018-8
Brackx F, De Knock B, De Schepper H: A matrix Hilbert transform in Hermitean Clifford analysis. J. Math. Anal. Appl. 2008, 344: 1068-1078. 10.1016/j.jmaa.2008.03.043
Kytmanov AM: The Bochner-Martinelli Integral and Its Applications. Brikhäuser, Basel; 1995.
Rocha-Chavez R, Shapiro M, Sommen F Res. Notes Math. 428. In Integral Theorem for Functions and Differential Forms in
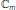 . Chapman & Hall/CRC, New York; 2002.
. Chapman & Hall/CRC, New York; 2002.Abreu Blaya R, Bory Reyes J, Brackx F, De Knock B, De Schepper H, Peña Peña D, Sommen F: Hermitean Cauchy integral decomposition of continuous functions on hypersurfaces. Bound. Value Probl. 2008., 2008: Article ID 425256
Abreu Blaya R, Bory Reyes J, Brackx F, De Schepper H, Sommen F: Boundary value problems associated to a Hermitian Helmholtz equation. J. Math. Anal. Appl. 2012, 389: 1268-1279. 10.1016/j.jmaa.2012.01.006
Gürlebeck K, Sprössig W: Quaternionic and Clifford Calculus for Physicists and Engineers. Wiley, Chichester; 1997.
Gürlebeck K, Habetha K, Sprössig W: Holomorphic Functions in the Plane and n-Dimensional Space. Birkhäuser, Basel; 2008.
Kravchenko VV, Shapiro MV Pitman Research in Mathematics Series 351. In Integral Representations for Spatial Models of Mathematical Physics. Longman, Harlow; 1996.
Acknowledgements
This paper is supported by National Natural Science Foundation of China (11271175), the AMEP, and DYSP of Linyi University. The authors would like to thank the referees for their valuable suggestion and comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the manuscript and typed, read, and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gu, L., Fu, Z. Riemann boundary value problem for H-2-monogenic function in Hermitian Clifford analysis. Bound Value Probl 2014, 81 (2014). https://doi.org/10.1186/1687-2770-2014-81
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2014-81
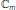 . Chapman & Hall/CRC, New York; 2002.
. Chapman & Hall/CRC, New York; 2002.