- Research Article
- Open access
- Published:
Entire Bounded Solutions for a Class of Quasilinear Elliptic Equations
Boundary Value Problems volume 2007, Article number: 016407 (2007)
Abstract
We consider the problem where
where is not identically zero. Under the condition that
is not identically zero. Under the condition that satisfies (H), we show that there exists
satisfies (H), we show that there exists such that the above-mentioned equation admits at least one solution for all
such that the above-mentioned equation admits at least one solution for all . This extends the results of Laplace equation to the case of
. This extends the results of Laplace equation to the case of -Laplace equation.
-Laplace equation.
References
Herrero MA, Vázquez JL: On the propagation properties of a nonlinear degenerate parabolic equation. Communications in Partial Differential Equations 1982,7(12):1381–1402. 10.1080/03605308208820255
Esteban JR, Vázquez JL: On the equation of turbulent filtration in one-dimensional porous media. Nonlinear Analysis 1986,10(11):1303–1325. 10.1016/0362-546X(86)90068-4
Yang Z: Existence of positive bounded entire solutions for quasilinear elliptic equations. Applied Mathematics and Computation 2004,156(3):743–754. 10.1016/j.amc.2003.06.024
Guedda M, Véron L: Local and global properties of solutions of quasilinear elliptic equations. Journal of Differential Equations 1988,76(1):159–189. 10.1016/0022-0396(88)90068-X
Guo ZM: Existence and uniqueness of positive radial solutions for a class of quasilinear elliptic equations. Applicable Analysis 1992,47(2–3):173–189.
Guo ZM: Some existence and multiplicity results for a class of quasilinear elliptic eigenvalue problems. Nonlinear Analysis 1992,18(10):957–971. 10.1016/0362-546X(92)90132-X
Guo ZM, Webb JRL: Uniqueness of positive solutions for quasilinear elliptic equations when a parameter is large. Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 1994,124(1):189–198. 10.1017/S0308210500029280
Lu Q, Yang Z, Twizell EH: Existence of entire explosive positive solutions of quasi-linear elliptic equations. Applied Mathematics and Computation 2004,148(2):359–372. 10.1016/S0096-3003(02)00852-4
Bognár G, Drábek P: The
 -Laplacian equation with superlinear and supercritical growth, multiplicity of radial solutions. Nonlinear Analysis 2005,60(4):719–728. 10.1016/j.na.2004.09.047
-Laplacian equation with superlinear and supercritical growth, multiplicity of radial solutions. Nonlinear Analysis 2005,60(4):719–728. 10.1016/j.na.2004.09.047Prashanth S, Sreenadh K: Multiplicity of positive solutions for
 -Laplace equation with superlinear-type nonlinearity. Nonlinear Analysis 2004,56(6):867–878. 10.1016/j.na.2003.10.026
-Laplace equation with superlinear-type nonlinearity. Nonlinear Analysis 2004,56(6):867–878. 10.1016/j.na.2003.10.026Brezis H, Kamin S: Sublinear elliptic equations in
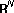 . Manuscripta Mathematica 1992,74(1):87–106. 10.1007/BF02567660
. Manuscripta Mathematica 1992,74(1):87–106. 10.1007/BF02567660Ambrosetti A, Brezis H, Cerami G: Combined effects of concave and convex nonlinearities in some elliptic problems. Journal of Functional Analysis 1994,122(2):519–543. 10.1006/jfan.1994.1078
Brezis H, Oswald L: Remarks on sublinear elliptic equations. Nonlinear Analysis 1986,10(1):55–64. 10.1016/0362-546X(86)90011-8
Bartsch T, Willem M: On an elliptic equation with concave and convex nonlinearities. Proceedings of the American Mathematical Society 1995,123(11):3555–3561. 10.1090/S0002-9939-1995-1301008-2
Ye D, Zhou F: Invariant criteria for existence of bounded positive solutions. Discrete and Continuous Dynamical Systems. Series A 2005,12(3):413–424.
El Mabrouk K: Entire bounded solutions for a class of sublinear elliptic equations. Nonlinear Analysis 2004,58(1–2):205–218. 10.1016/j.na.2004.01.004
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, Z., Xu, B. Entire Bounded Solutions for a Class of Quasilinear Elliptic Equations. Bound Value Probl 2007, 016407 (2007). https://doi.org/10.1155/2007/16407
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/16407
 -Laplacian equation with superlinear and supercritical growth, multiplicity of radial solutions. Nonlinear Analysis 2005,60(4):719–728. 10.1016/j.na.2004.09.047
-Laplacian equation with superlinear and supercritical growth, multiplicity of radial solutions. Nonlinear Analysis 2005,60(4):719–728. 10.1016/j.na.2004.09.047 -Laplace equation with superlinear-type nonlinearity. Nonlinear Analysis 2004,56(6):867–878. 10.1016/j.na.2003.10.026
-Laplace equation with superlinear-type nonlinearity. Nonlinear Analysis 2004,56(6):867–878. 10.1016/j.na.2003.10.026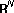 . Manuscripta Mathematica 1992,74(1):87–106. 10.1007/BF02567660
. Manuscripta Mathematica 1992,74(1):87–106. 10.1007/BF02567660