- Research Article
- Open access
- Published:
Several Existence Theorems of Monotone Positive Solutions for Third-Order Multipoint Boundary Value Problems
Boundary Value Problems volume 2007, Article number: 017951 (2008)
Abstract
Using fixed point index theory, we obtain several sufficient conditions of existence of at least one positive solution for third-order -point boundary value problems.
-point boundary value problems.
References
Zhang X, Liu L, Wu C: Nontrivial solution of third-order nonlinear eigenvalue problems. Applied Mathematics and Computation 2006,176(2):714–721. 10.1016/j.amc.2005.10.017
Guo L-J, Sun J-P, Zhao Y-H: Existence of positive solutions for nonlinear third-order three-point boundary value problems . to appear in Nonlinear Analysis: Theory, Methods & Applications
Du Z, Ge W, Lin X: Existence of solutions for a class of third-order nonlinear boundary value problems. Journal of Mathematical Analysis and Applications 2004,294(1):104–112. 10.1016/j.jmaa.2004.02.001
Cabada A, Minhós F, Santos AI: Solvability for a third order discontinuous fully equation with nonlinear functional boundary conditions. Journal of Mathematical Analysis and Applications 2006,322(2):735–748. 10.1016/j.jmaa.2005.09.065
Jiang D, Agarwal RP: A uniqueness and existence theorem for a singular third-order boundary value problem on
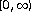 . Applied Mathematics Letters 2002,15(4):445–451. 10.1016/S0893-9659(01)00157-4
. Applied Mathematics Letters 2002,15(4):445–451. 10.1016/S0893-9659(01)00157-4Anderson D, Avery RI: Multiple positive solutions to a third-order discrete focal boundary value problem. Computers & Mathematics with Applications 2001,42(3–5):333–340.
Wang J, Gao W, Zhang Z: Singular nonlinear boundary value problems arising in boundary layer theory. Journal of Mathematical Analysis and Applications 1999,233(1):246–256. 10.1006/jmaa.1999.6290
Paatashvili V, Samko S: Boundary value problems for analytic functions in the class of Cauchy-type integrals with density in
 . Boundary Value Problem 2005,2005(1):43–71. 10.1155/BVP.2005.43
. Boundary Value Problem 2005,2005(1):43–71. 10.1155/BVP.2005.43Agarwal RP, Kiguradze I: Two-point boundary value problems for higher-order linear differential equations with strong singularities. Boundary Value Problems 2006, 2006: 32 pages.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiang, W., Li, F. Several Existence Theorems of Monotone Positive Solutions for Third-Order Multipoint Boundary Value Problems. Bound Value Probl 2007, 017951 (2008). https://doi.org/10.1155/2007/17951
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/17951
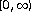 . Applied Mathematics Letters 2002,15(4):445–451. 10.1016/S0893-9659(01)00157-4
. Applied Mathematics Letters 2002,15(4):445–451. 10.1016/S0893-9659(01)00157-4 . Boundary Value Problem 2005,2005(1):43–71. 10.1155/BVP.2005.43
. Boundary Value Problem 2005,2005(1):43–71. 10.1155/BVP.2005.43