- Research Article
- Open access
- Published:
Symmetry Theorems and Uniform Rectifiability
Boundary Value Problems volume 2007, Article number: 030190 (2006)
Abstract
We study overdetermined boundary conditions for positive solutions to some elliptic partial differential equations of -Laplacian type in a bounded domain
-Laplacian type in a bounded domain . We show that these conditions imply uniform rectifiability of
. We show that these conditions imply uniform rectifiability of and also that they yield the solution to certain symmetry problems.
and also that they yield the solution to certain symmetry problems.
References
David G, Semmes S: Singular integrals and rectifiable sets in: Beyond Lipschitz graphs. Astérisque 1991, (193):152.
David G, Semmes S: Analysis of and on Uniformly Rectifiable Sets, Mathematical Surveys and Monographs. Volume 38. American Mathematical Society, Rhode Island; 1993:xii+356.
Serrin J: A symmetry problem in potential theory. Archive for Rational Mechanics and Analysis 1971,43(4):304–318.
Lewis JL, Vogel AL: On some almost everywhere symmetry theorems. In Nonlinear Diffusion Equations and Their Equilibrium States, 3 (Gregynog, 1989), Progr. Nonlinear Differential Equations Appl.. Volume 7. Birkhäuser Boston, Massachusetts; 1992:347–374.
Lewis JL, Vogel AL: A symmetry theorem revisited. Proceedings of the American Mathematical Society 2002,130(2):443–451. 10.1090/S0002-9939-01-06200-1
Lewis JL, Vogel AL: Uniqueness in a free boundary problem. Communications in Partial Differential Equations 2006, 31: 1591–1614. 10.1080/03605300500455909
Vogel AL: Symmetry and regularity for general regions having a solution to certain overdetermined boundary value problems. Atti del Seminario Matematico e Fisico dell'Università di Modena 1992,40(2):443–484.
Lewis JL, Vogel AL: On pseudospheres that are quasispheres. Revista Matemática Iberoamericana 2001,17(2):221–255.
Bennewitz B: Nonuniqueness in a free boundary problem, Ph.D. thesis. University of Kentucky, Lexington KY; 2006.
Henrot A, Shahgholian H: Existence of classical solutions to a free boundary problem for the
 -Laplace operator. I. The exterior convex case. Journal für die reine und angewandte Mathematik 2000, 521: 85–97.
-Laplace operator. I. The exterior convex case. Journal für die reine und angewandte Mathematik 2000, 521: 85–97.Henrot A, Shahgholian H: Existence of classical solutions to a free boundary problem for the
 -Laplace operator. II. The interior convex case. Indiana University Mathematics Journal 2000,49(1):311–323.
-Laplace operator. II. The interior convex case. Indiana University Mathematics Journal 2000,49(1):311–323.Henrot A, Shahgholian H: The one phase free boundary problem for the
 -Laplacian with non-constant Bernoulli boundary condition. Transactions of the American Mathematical Society 2002,354(6):2399–2416. 10.1090/S0002-9947-02-02892-1
-Laplacian with non-constant Bernoulli boundary condition. Transactions of the American Mathematical Society 2002,354(6):2399–2416. 10.1090/S0002-9947-02-02892-1Bishop CJ, Jones PW: Harmonic measure and arclength. Annals of Mathematics. Second Series 1990,132(3):511–547. 10.2307/1971428
David G, Jerison D: Lipschitz approximation to hypersurfaces, harmonic measure, and singular integrals. Indiana University Mathematics Journal 1990,39(3):831–845. 10.1512/iumj.1990.39.39040
Kenig CE, Pipher J: The Dirichlet problem for elliptic equations with drift terms. Publicacions Matemàtiques 2001,45(1):199–217.
Alt HW, Caffarelli LA, Friedman A: A free boundary problem for quasilinear elliptic equations. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1984,11(1):1–44.
Serrin J: Local behavior of solutions of quasi-linear equations. Acta Mathematica 1964,111(1):247–302. 10.1007/BF02391014
Garofalo N, Lewis JL: A symmetry result related to some overdetermined boundary value problems. American Journal of Mathematics 1989,111(1):9–33. 10.2307/2374477
Choe HJ: Regularity for minimizers of certain degenerate functionals with nonstandard growth conditions. Communications in Partial Differential Equations 1991,16(2–3):363–372. 10.1080/03605309108820762
Manfredi JJ: Regularity for minima of functionals with
 -growth. Journal of Differential Equations 1988,76(2):203–212. 10.1016/0022-0396(88)90070-8
-growth. Journal of Differential Equations 1988,76(2):203–212. 10.1016/0022-0396(88)90070-8Heinonen J, Kilpeläinen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. Oxford University Press, New York; 1993:vi+363.
Kilpeläinen T, Zhong X: Growth of entire
 -subharmonic functions. Annales Academiæ Scientiarium Fennicæ. Mathematica 2003,28(1):181–192.
-subharmonic functions. Annales Academiæ Scientiarium Fennicæ. Mathematica 2003,28(1):181–192.Kilpeläinen T, Malý J: The Wiener test and potential estimates for quasilinear elliptic equations. Acta Mathematica 1994,172(1):137–161. 10.1007/BF02392793
Eremenko A, Lewis JL: Uniform limits of certain
 -harmonic functions with applications to quasiregular mappings. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1991,16(2):361–375.
-harmonic functions with applications to quasiregular mappings. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1991,16(2):361–375.Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Fundamental Principles of Mathematical Sciences. Volume 224. 2nd edition. Springer, Berlin; 1983.
Mattila P: Geometry of Sets and Measures in Euclidean Spaces, Cambridge Studies in Advanced Mathematics. Volume 44. Cambridge University Press, Cambridge; 1995:xii+343.
Semmes S: Differentiable function theory on hypersurfaces in
 (without bounds on their smoothness). Indiana University Mathematics Journal 1990,39(4):985–1004. 10.1512/iumj.1990.39.39047
(without bounds on their smoothness). Indiana University Mathematics Journal 1990,39(4):985–1004. 10.1512/iumj.1990.39.39047Littman W, Stampacchia G, Weinberger HF: Regular points for elliptic equations with discontinuous coefficients. Annali della Scuola Normale Superiore di Pisa. Serie III 1963, 17: 43–77.
Gariepy R, Ziemer WP: A regularity condition at the boundary for solutions of quasilinear elliptic equations. Archive for Rational Mechanics and Analysis 1977,67(1):25–39. 10.1007/BF00280825
Hofmann S, Lewis JL: The Dirichlet problem for parabolic operators with singular drift terms. Memoirs of the American Mathematical Society 2001,151(719):viii+113.
Rivera-Noriega J: Absolute continuity of parabolic measure and area integral estimates in non-cylindrical domains. Indiana University Mathematics Journal 2003,52(2):477–525.
Bennewitz B, Lewis JL: On weak reverse Hölder inequalities for nondoubling harmonic measures. Complex Variables 2004,49(7–9):571–582.
Gehring FW: The
 -integrability of the partial derivatives of a quasiconformal mapping. Acta Mathematica 1973,130(1):265–277. 10.1007/BF02392268
-integrability of the partial derivatives of a quasiconformal mapping. Acta Mathematica 1973,130(1):265–277. 10.1007/BF02392268Danielli D, Petrosyan A: A minimum problem with free boundary for a degenerate quasilinear operator. Calculus of Variations and Partial Differential Equations 2005,23(1):97–124. 10.1007/s00526-004-0294-5
Mattila P, Melnikov MS, Verdera J: The Cauchy integral, analytic capacity, and uniform rectifiability. Annals of Mathematics. Second Series 1996,144(1):127–136. 10.2307/2118585
Lewis JL: Uniformly fat sets. Transactions of the American Mathematical Society 1988,308(1):177–196. 10.1090/S0002-9947-1988-0946438-4
Mateu J, Tolsa X, Verdera J: The planar Cantor sets of zero analytic capacity and the local
 -theorem. Journal of the American Mathematical Society 2003,16(1):19–28. 10.1090/S0894-0347-02-00401-0
-theorem. Journal of the American Mathematical Society 2003,16(1):19–28. 10.1090/S0894-0347-02-00401-0Nazarov F, Treil S, Volberg A: Accretive system
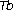 -theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4
-theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4Tolsa X: Painlevé's problem and the semiadditivity of analytic capacity. Acta Mathematica 2003,190(1):105–149. 10.1007/BF02393237
Tolsa X: The space
 for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8
for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8Feldman M: Regularity of Lipschitz free boundaries in two-phase problems for fully nonlinear elliptic equations. Indiana University Mathematics Journal 2001,50(3):1171–1200.
Wang P-Y: Regularity of free boundaries of two-phase problems for fully nonlinear elliptic equations of second order. I. Lipschitz free boundaries are
 Communications on Pure and Applied Mathematics 2000,53(7):799–810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q
Communications on Pure and Applied Mathematics 2000,53(7):799–810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lewis, J.L., Vogel, A.L. Symmetry Theorems and Uniform Rectifiability. Bound Value Probl 2007, 030190 (2006). https://doi.org/10.1155/2007/30190
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/30190
 -Laplace operator. I. The exterior convex case. Journal für die reine und angewandte Mathematik 2000, 521: 85–97.
-Laplace operator. I. The exterior convex case. Journal für die reine und angewandte Mathematik 2000, 521: 85–97. -Laplace operator. II. The interior convex case. Indiana University Mathematics Journal 2000,49(1):311–323.
-Laplace operator. II. The interior convex case. Indiana University Mathematics Journal 2000,49(1):311–323. -Laplacian with non-constant Bernoulli boundary condition. Transactions of the American Mathematical Society 2002,354(6):2399–2416. 10.1090/S0002-9947-02-02892-1
-Laplacian with non-constant Bernoulli boundary condition. Transactions of the American Mathematical Society 2002,354(6):2399–2416. 10.1090/S0002-9947-02-02892-1 -growth. Journal of Differential Equations 1988,76(2):203–212. 10.1016/0022-0396(88)90070-8
-growth. Journal of Differential Equations 1988,76(2):203–212. 10.1016/0022-0396(88)90070-8 -subharmonic functions. Annales Academiæ Scientiarium Fennicæ. Mathematica 2003,28(1):181–192.
-subharmonic functions. Annales Academiæ Scientiarium Fennicæ. Mathematica 2003,28(1):181–192. -harmonic functions with applications to quasiregular mappings. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1991,16(2):361–375.
-harmonic functions with applications to quasiregular mappings. Annales Academiae Scientiarum Fennicae. Series A I. Mathematica 1991,16(2):361–375. (without bounds on their smoothness). Indiana University Mathematics Journal 1990,39(4):985–1004. 10.1512/iumj.1990.39.39047
(without bounds on their smoothness). Indiana University Mathematics Journal 1990,39(4):985–1004. 10.1512/iumj.1990.39.39047 -integrability of the partial derivatives of a quasiconformal mapping. Acta Mathematica 1973,130(1):265–277. 10.1007/BF02392268
-integrability of the partial derivatives of a quasiconformal mapping. Acta Mathematica 1973,130(1):265–277. 10.1007/BF02392268 -theorem. Journal of the American Mathematical Society 2003,16(1):19–28. 10.1090/S0894-0347-02-00401-0
-theorem. Journal of the American Mathematical Society 2003,16(1):19–28. 10.1090/S0894-0347-02-00401-0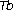 -theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4
-theorems on nonhomogeneous spaces. Duke Mathematical Journal 2002,113(2):259–312. 10.1215/S0012-7094-02-11323-4 for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8
for nondoubling measures in terms of a grand maximal operator. Transactions of the American Mathematical Society 2003,355(1):315–348. 10.1090/S0002-9947-02-03131-8 Communications on Pure and Applied Mathematics 2000,53(7):799–810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q
Communications on Pure and Applied Mathematics 2000,53(7):799–810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q