- Research Article
- Open access
- Published:
Existence of Positive Solutions for Boundary Value Problems of Nonlinear Functional Difference Equation with  -Laplacian Operator
-Laplacian Operator
Boundary Value Problems volume 2007, Article number: 038230 (2007)
Abstract
The existence of positive solutions for boundary value problems of nonlinear functional difference equations with -Laplacian operator is investigated. Sufficient conditions are obtained for the existence of at least one positive solution and two positive solutions.
-Laplacian operator is investigated. Sufficient conditions are obtained for the existence of at least one positive solution and two positive solutions.
References
Erbe LH, Wang H: On the existence of positive solutions of ordinary differential equations. Proceedings of the American Mathematical Society 1994,120(3):743–748. 10.1090/S0002-9939-1994-1204373-9
Grimm LJ, Schmitt K: Boundary value problems for differential equations with deviating arguments. Aequationes Mathematicae 1970,4(1–2):176–190. 10.1007/BF01817758
Gustafson GB, Schmitt K: Nonzero solutions of boundary value problems for second order ordinary and delay-differential equations. Journal of Differential Equations 1972,12(1):129–147. 10.1016/0022-0396(72)90009-5
Weng PX, Jiang D: Existence of positive solutions for boundary value problem of second-order FDE. Computers & Mathematics with Applications 1999,37(10):1–9. 10.1016/S0898-1221(99)00120-0
Weng PX, Tian Y: Existence of positive solution for singular
 conjugate boundary value problem with delay. Far East Journal of Mathematical Sciences 1999,1(3):367–382.
conjugate boundary value problem with delay. Far East Journal of Mathematical Sciences 1999,1(3):367–382.Wong F-H: Existence of positive solutions for
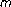 -Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11–17. 10.1016/S0893-9659(98)00164-5
-Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11–17. 10.1016/S0893-9659(98)00164-5Yang SJ, Shi B, Gai MJ: Boundary value problems for functional differential systems. Indian Journal of Pure and Applied Mathematics 2005,36(12):685–705.
Weng PX, Guo ZH: Existence of positive solutions to BVPs for a nonlinear functional difference equation with
 -Laplacian operator. Acta Mathematica Sinica 2006,49(1):187–194.
-Laplacian operator. Acta Mathematica Sinica 2006,49(1):187–194.Ntouyas SK, Sficas YG, Tsamatos PCh: Boundary value problems for functional-differential equations. Journal of Mathematical Analysis and Applications 1996,199(1):213–230. 10.1006/jmaa.1996.0137
Guo DJ: Nonlinear Functional Analysis. Shandong Scientific Press, Jinan, China; 1985.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, S., Shi, B. & Zhang, D. Existence of Positive Solutions for Boundary Value Problems of Nonlinear Functional Difference Equation with  -Laplacian Operator.
Bound Value Probl 2007, 038230 (2007). https://doi.org/10.1155/2007/38230
-Laplacian Operator.
Bound Value Probl 2007, 038230 (2007). https://doi.org/10.1155/2007/38230
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/38230
 conjugate boundary value problem with delay. Far East Journal of Mathematical Sciences 1999,1(3):367–382.
conjugate boundary value problem with delay. Far East Journal of Mathematical Sciences 1999,1(3):367–382.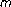 -Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11–17. 10.1016/S0893-9659(98)00164-5
-Laplacian boundary value problems. Applied Mathematics Letters 1999,12(3):11–17. 10.1016/S0893-9659(98)00164-5 -Laplacian operator. Acta Mathematica Sinica 2006,49(1):187–194.
-Laplacian operator. Acta Mathematica Sinica 2006,49(1):187–194.