- Research Article
- Open access
- Published:
Subsolutions of Elliptic Operators in Divergence Form and Application to Two-Phase Free Boundary Problems
Boundary Value Problems volume 2007, Article number: 057049 (2006)
Abstract
Let be a divergence form operator with Lipschitz continuous coefficients in a domain
be a divergence form operator with Lipschitz continuous coefficients in a domain , and let
, and let be a continuous weak solution of
be a continuous weak solution of in
in . In this paper, we show that if
. In this paper, we show that if satisfies a suitable differential inequality, then
satisfies a suitable differential inequality, then is a subsolution of
is a subsolution of away from its zero set. We apply this result to prove
away from its zero set. We apply this result to prove regularity of Lipschitz free boundaries in two-phase problems.
regularity of Lipschitz free boundaries in two-phase problems.
References
Caffarelli LA:A Harnack inequality approach to the regularity of free boundaries. I. Lipschitz free boundaries are
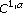 . Revista Matemática Iberoamericana 1987,3(2):139-162.
. Revista Matemática Iberoamericana 1987,3(2):139-162.Feldman M: Regularity for nonisotropic two-phase problems with Lipschitz free boundaries. Differential and Integral Equations 1997,10(6):1171-1179.
Wang P-Y:Regularity of free boundaries of two-phase problems for fully nonlinear elliptic equations of second order. I. Lipschitz free boundaries are
 . Communications on Pure and Applied Mathematics 2000,53(7):799-810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q
. Communications on Pure and Applied Mathematics 2000,53(7):799-810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-QFeldman M: Regularity of Lipschitz free boundaries in two-phase problems for fully nonlinear elliptic equations. Indiana University Mathematics Journal 2001,50(3):1171-1200.
Cerutti MC, Ferrari F, Salsa S:Two-phase problems for linear elliptic operators with variable coefficients: Lipschitz free boundaries are
 . Archive for Rational Mechanics and Analysis 2004,171(3):329-348. 10.1007/s00205-003-0290-5
. Archive for Rational Mechanics and Analysis 2004,171(3):329-348. 10.1007/s00205-003-0290-5Ferrari F:Two-phase problems for a class of fully nonlinear elliptic operators. Lipschitz free boundaries are
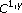 . American Journal of Mathematics 2006,128(3):541-571. 10.1353/ajm.2006.0023
. American Journal of Mathematics 2006,128(3):541-571. 10.1353/ajm.2006.0023Caffarelli LA: A Harnack inequality approach to the regularity of free boundaries. II. Flat free boundaries are Lipschitz. Communications on Pure and Applied Mathematics 1989,42(1):55-78. 10.1002/cpa.3160420105
Caffarelli LA, Fabes E, Mortola S, Salsa S: Boundary behavior of nonnegative solutions of elliptic operators in divergence form. Indiana University Mathematics Journal 1981,30(4):621-640. 10.1512/iumj.1981.30.30049
Jerison DS, Kenig CE: Boundary behavior of harmonic functions in nontangentially accessible domains. Advances in Mathematics 1982,46(1):80-147. 10.1016/0001-8708(82)90055-X
Brelot M: Axiomatique des Fonctions Harmoniques, Séminaire de Mathématiques Supérieures - Été 1965. Les Presses de l'Université de Montréal, Quebec; 1966.
Hervé R-M: Recherches axiomatiques sur la théorie des fonctions surharmoniques et du potentiel. Annales de l'Institut Fourier. Université de Grenoble 1962, 12: 415-571.
Hervé R-M:Un principe du maximum pour les sous-solutions locales d'une équation uniformément elliptique de la forme
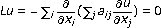 . Annales de l'Institut Fourier. Université de Grenoble 1964,14(2):493-507. 10.5802/aif.185
. Annales de l'Institut Fourier. Université de Grenoble 1964,14(2):493-507. 10.5802/aif.185Hervé R-M, Hervé M: Les fonctions surharmoniques associées à un opérateur elliptique du second ordre à coefficients discontinus. Annales de l'Institut Fourier. Université de Grenoble 1969,19(1):305-359. 10.5802/aif.320
Littman W, Stampacchia G, Weinberger HF: Regular points for elliptic equations with discontinuous coefficients. Annali della Scuola Normale Superiore di Pisa, Serie III 1963, 17: 43-77.
Hervé R-M:Quelques propriétés des fonctions surharmoniques associées à une équation uniformément elliptique de la form
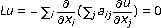 . Annales de l'Institut Fourier. Université de Grenoble 1965,15(2):215-223. 10.5802/aif.214
. Annales de l'Institut Fourier. Université de Grenoble 1965,15(2):215-223. 10.5802/aif.214Caffarelli LA:A Harnack inequality approach to the regularity of free boundaries. III. Existence theory, compactness, and dependence on
 . Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1988,15(4):583-602 (1989).
. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1988,15(4):583-602 (1989).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ferrari, F., Salsa, S. Subsolutions of Elliptic Operators in Divergence Form and Application to Two-Phase Free Boundary Problems. Bound Value Probl 2007, 057049 (2006). https://doi.org/10.1155/2007/57049
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/57049
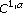 . Revista Matemática Iberoamericana 1987,3(2):139-162.
. Revista Matemática Iberoamericana 1987,3(2):139-162. . Communications on Pure and Applied Mathematics 2000,53(7):799-810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q
. Communications on Pure and Applied Mathematics 2000,53(7):799-810. 10.1002/(SICI)1097-0312(200007)53:7<799::AID-CPA1>3.0.CO;2-Q . Archive for Rational Mechanics and Analysis 2004,171(3):329-348. 10.1007/s00205-003-0290-5
. Archive for Rational Mechanics and Analysis 2004,171(3):329-348. 10.1007/s00205-003-0290-5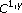 . American Journal of Mathematics 2006,128(3):541-571. 10.1353/ajm.2006.0023
. American Journal of Mathematics 2006,128(3):541-571. 10.1353/ajm.2006.0023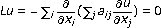 . Annales de l'Institut Fourier. Université de Grenoble 1964,14(2):493-507. 10.5802/aif.185
. Annales de l'Institut Fourier. Université de Grenoble 1964,14(2):493-507. 10.5802/aif.185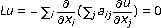 . Annales de l'Institut Fourier. Université de Grenoble 1965,15(2):215-223. 10.5802/aif.214
. Annales de l'Institut Fourier. Université de Grenoble 1965,15(2):215-223. 10.5802/aif.214 . Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1988,15(4):583-602 (1989).
. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1988,15(4):583-602 (1989).