- Research Article
- Open access
- Published:
A Boundary Harnack Principle for Infinity-Laplacian and Some Related Results
Boundary Value Problems volume 2007, Article number: 078029 (2007)
Abstract
We prove a boundary comparison principle for positive infinity-harmonic functions for smooth boundaries. As consequences, we obtain (a) a doubling property for certain positive infinity-harmonic functions in smooth bounded domains and the half-space, and (b) the optimality of blowup rates of Aronsson's examples of singular solutions in cones.
References
Bhattacharya T:On the properties of
 -harmonic functions and an application to capacitary convex rings. Electronic Journal of Differential Equations 2002,2002(101):1-22.
-harmonic functions and an application to capacitary convex rings. Electronic Journal of Differential Equations 2002,2002(101):1-22.Bauman P: Positive solutions of elliptic equations in nondivergence form and their adjoints. Arkiv för Matematik 1984,22(2):153-173. 10.1007/BF02384378
Caffarelli L, Fabes E, Mortola S, Salsa S: Boundary behavior of nonnegative solutions of elliptic operators in divergence form. Indiana University Mathematics Journal 1981,30(4):621-640. 10.1512/iumj.1981.30.30049
Fabes E, Garofalo N, Marín-Malave S, Salsa S: Fatou theorems for some nonlinear elliptic equations. Revista Matemática Iberoamericana 1988,4(2):227-251.
Manfredi JJ, Weitsman A:On the Fatou theorem for
 -harmonic functions. Communications in Partial Differential Equations 1988,13(6):651-668. 10.1080/03605308808820556
-harmonic functions. Communications in Partial Differential Equations 1988,13(6):651-668. 10.1080/03605308808820556Aronsson G:Construction of singular solutions to the
 -harmonic equation and its limit equation for
-harmonic equation and its limit equation for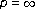 . Manuscripta Mathematica 1986,56(2):135-158. 10.1007/BF01172152
. Manuscripta Mathematica 1986,56(2):135-158. 10.1007/BF01172152Bhattacharya T: A note on non-negative singular infinity-harmonic functions in the half-space. Revista Matemática Complutense 2005,18(2):377-385.
Aronsson G, Crandall MG, Juutinen P: A tour of the theory of absolutely minimizing functions. Bulletin of the American Mathematical Society. New Series 2004,41(4):439-505. 10.1090/S0273-0979-04-01035-3
Crandall MG, Evans LC, Gariepy RF: Optimal Lipschitz extensions and the infinity Laplacian. Calculus of Variations and Partial Differential Equations 2001,13(2):123-139.
Bhattacharya T, DiBenedetto E, Manfredi JJ:Limits as
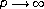 of
of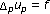 and related extremal problems. Some topics in nonlinear PDEs (Turin, 1989). Rendiconti del Seminario Matematico. Università e Politecnico di Torino 1989, 15-68 (1991). special issue
and related extremal problems. Some topics in nonlinear PDEs (Turin, 1989). Rendiconti del Seminario Matematico. Università e Politecnico di Torino 1989, 15-68 (1991). special issueBhattacharya T:On the behaviour of
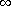 -harmonic functions near isolated points. Nonlinear Analysis. Theory, Methods & Applications 2004,58(3-4):333-349. 10.1016/j.na.2004.02.028
-harmonic functions near isolated points. Nonlinear Analysis. Theory, Methods & Applications 2004,58(3-4):333-349. 10.1016/j.na.2004.02.028Bhattacharya T:On the behaviour of
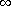 -harmonic functions on some special unbounded domains. Pacific Journal of Mathematics 2005,219(2):237-253. 10.2140/pjm.2005.219.237
-harmonic functions on some special unbounded domains. Pacific Journal of Mathematics 2005,219(2):237-253. 10.2140/pjm.2005.219.237Lindqvist P, Manfredi JJ:The Harnack inequality for
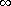 -harmonic functions. Electronic Journal of Differential Equations 1995,1995(4):1-5.
-harmonic functions. Electronic Journal of Differential Equations 1995,1995(4):1-5.Savin O:
 regularity for infinity harmonic functions in two dimensions. Archive for Rational Mechanics and Analysis 2005,176(3):351-361. 10.1007/s00205-005-0355-8
regularity for infinity harmonic functions in two dimensions. Archive for Rational Mechanics and Analysis 2005,176(3):351-361. 10.1007/s00205-005-0355-8Barles G, Busca J: Existence and comparison results for fully nonlinear degenerate elliptic equations without zeroth-order term. Communications in Partial Differential Equations 2001,26(11-12):2323-2337. 10.1081/PDE-100107824
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bhattacharya, T. A Boundary Harnack Principle for Infinity-Laplacian and Some Related Results. Bound Value Probl 2007, 078029 (2007). https://doi.org/10.1155/2007/78029
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/78029
 -harmonic functions and an application to capacitary convex rings. Electronic Journal of Differential Equations 2002,2002(101):1-22.
-harmonic functions and an application to capacitary convex rings. Electronic Journal of Differential Equations 2002,2002(101):1-22. -harmonic functions. Communications in Partial Differential Equations 1988,13(6):651-668. 10.1080/03605308808820556
-harmonic functions. Communications in Partial Differential Equations 1988,13(6):651-668. 10.1080/03605308808820556 -harmonic equation and its limit equation for
-harmonic equation and its limit equation for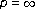 . Manuscripta Mathematica 1986,56(2):135-158. 10.1007/BF01172152
. Manuscripta Mathematica 1986,56(2):135-158. 10.1007/BF01172152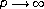 of
of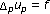 and related extremal problems. Some topics in nonlinear PDEs (Turin, 1989). Rendiconti del Seminario Matematico. Università e Politecnico di Torino 1989, 15-68 (1991). special issue
and related extremal problems. Some topics in nonlinear PDEs (Turin, 1989). Rendiconti del Seminario Matematico. Università e Politecnico di Torino 1989, 15-68 (1991). special issue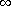 -harmonic functions near isolated points. Nonlinear Analysis. Theory, Methods & Applications 2004,58(3-4):333-349. 10.1016/j.na.2004.02.028
-harmonic functions near isolated points. Nonlinear Analysis. Theory, Methods & Applications 2004,58(3-4):333-349. 10.1016/j.na.2004.02.028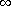 -harmonic functions on some special unbounded domains. Pacific Journal of Mathematics 2005,219(2):237-253. 10.2140/pjm.2005.219.237
-harmonic functions on some special unbounded domains. Pacific Journal of Mathematics 2005,219(2):237-253. 10.2140/pjm.2005.219.237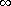 -harmonic functions. Electronic Journal of Differential Equations 1995,1995(4):1-5.
-harmonic functions. Electronic Journal of Differential Equations 1995,1995(4):1-5. regularity for infinity harmonic functions in two dimensions. Archive for Rational Mechanics and Analysis 2005,176(3):351-361. 10.1007/s00205-005-0355-8
regularity for infinity harmonic functions in two dimensions. Archive for Rational Mechanics and Analysis 2005,176(3):351-361. 10.1007/s00205-005-0355-8