- Research Article
- Open access
- Published:
Existence and Nonexistence Results for a Class of Quasilinear Elliptic Systems
Boundary Value Problems volume 2007, Article number: 085621 (2007)
Abstract
Using variational methods, we prove the existence and nonexistence of positive solutions for a class of -Laplacian systems with a parameter.
-Laplacian systems with a parameter.
References
Perera K: Multiple positive solutions for a class of quasilinear elliptic boundary-value problems. Electronic Journal of Differential Equations 2003, (7):5.
Maya C, Shivaji R: Multiple positive solutions for a class of semilinear elliptic boundary value problems. Nonlinear Analysis 1999,38(4):497-504. 10.1016/S0362-546X(98)00211-9
de Thélin F: Première valeur propre d'un système elliptique non linéaire. Comptes Rendus de l'Académie des Sciences 1990,311(10):603-606.
Anane A:Simplicité et isolation de la première valeur propre du
 -laplacien avec poids. Comptes Rendus des Séances de l'Académie des Sciences 1987,305(16):725-728.
-laplacien avec poids. Comptes Rendus des Séances de l'Académie des Sciences 1987,305(16):725-728.DiBenedetto E:
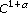 local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis 1983,7(8):827-850. 10.1016/0362-546X(83)90061-5
local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis 1983,7(8):827-850. 10.1016/0362-546X(83)90061-5Trudinger NS: On Harnack type inequalities and their application to quasilinear elliptic equations. Communications on Pure and Applied Mathematics 1967,20(4):721-747. 10.1002/cpa.3160200406
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. American Mathematical Society, Washington, DC, USA; 1986:viii+100.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
El Manouni, S., Perera, K. Existence and Nonexistence Results for a Class of Quasilinear Elliptic Systems. Bound Value Probl 2007, 085621 (2007). https://doi.org/10.1155/2007/85621
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/85621
 -laplacien avec poids. Comptes Rendus des Séances de l'Académie des Sciences 1987,305(16):725-728.
-laplacien avec poids. Comptes Rendus des Séances de l'Académie des Sciences 1987,305(16):725-728.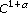 local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis 1983,7(8):827-850. 10.1016/0362-546X(83)90061-5
local regularity of weak solutions of degenerate elliptic equations. Nonlinear Analysis 1983,7(8):827-850. 10.1016/0362-546X(83)90061-5