- Research Article
- Open access
- Published:
Solvability of Second-Order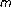 -Point Boundary Value Problems with Impulses
-Point Boundary Value Problems with Impulses
Boundary Value Problems volume 2007, Article number: 097067 (2007)
Abstract
By Leray-Schauder continuation theorem and the nonlinear alternative of Leray-Schauder type, the existence of a solution for an -point boundary value problem with impulses is proved.
-point boundary value problem with impulses is proved.
References
Gupta CP: Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. Journal of Mathematical Analysis and Applications 1992,168(2):540-551. 10.1016/0022-247X(92)90179-H
Gupta CP, Ntouyas SK, Tsamatos PCh:Solvability of an
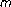 -point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036
-point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036Ma R:Existence of positive solutions for superlinear semipositone
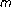 -point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391
-point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391Agarwal RP, O'Regan D: A multiplicity result for second order impulsive differential equations via the Leggett Williams fixed point theorem. Applied Mathematics and Computation 2005,161(2):433-439. 10.1016/j.amc.2003.12.096
Mawhin J: Topological Degree Methods in Nonlinear Boundary Value Problems, CBMS Regional Conference Series in Mathematics. Volume 40. American Mathematical Society, Providence, RI, USA; 1979:v+122.
Agarwal RP, O'Regan D, Wong PJY: Positive Solutions of Differential, Difference and Integral Equations. Kluwer Academic, Dordrecht, The Netherlands; 1999:xii+417.
Baĭnov DD, Simeonov PS: Impulsive Differential Equations: Periodic Solutions and Applications, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 66. Longman Scientific & Technical, Harlow, UK; 1993:x+228.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, J., Liu, S. Solvability of Second-Order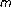 -Point Boundary Value Problems with Impulses.
Bound Value Probl 2007, 097067 (2007). https://doi.org/10.1155/2007/97067
-Point Boundary Value Problems with Impulses.
Bound Value Probl 2007, 097067 (2007). https://doi.org/10.1155/2007/97067
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/97067
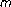 -point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036
-point boundary value problem for second order ordinary differential equations. Journal of Mathematical Analysis and Applications 1995,189(2):575-584. 10.1006/jmaa.1995.1036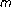 -point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391
-point boundary-value problems. Proceedings of the Edinburgh Mathematical Society. Series II 2003,46(2):279-292. 10.1017/S0013091502000391