- Research Article
- Open access
- Published:
Multiplicity Results via Topological Degree for Impulsive Boundary Value Problems under Non-Well-Ordered Upper and Lower Solution Conditions
Boundary Value Problems volume 2008, Article number: 197205 (2008)
Abstract
Some multiplicity results for solutions of an impulsive boundary value problem are obtained under the condition of non-well-ordered upper and lower solutions. The main ideas of this paper are to associate a Leray-Schauder degree with the lower or upper solution.
1. Introduction
In this paper, we study multiplicity of solutions of the impulsive boundary value problem

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Impulsive differential equations arise naturally in a wide variety of applications, such as spacecraft control, inspection processes in operations research, drug administration, and threshold theory in biology. In the past twenty years, a significant development in the theory of impulsive differential equations was seen. Many authors have studied impulsive differential equations using a variety of methods (see [1–5] and the references therein).
The purpose of this paper is to study the multiplicity of solutions of the impulsive boundary value problems (1.1) by the method of upper and lower solutions. The method of lower and upper solutions has a very long history. Some of the ideas can be traced back to Picard [6]. This method deals mainly with existence results for various boundary value problems. For an overview of this method for ordinary differential equations, the reader is referred to [7]. Usually, when one uses the method of upper and lower solutions to study the existence and multiplicity of solutions of impulsive differential equations, one assumes that the upper solution is larger than the lower solution, that is, the condition that upper and lower solutions are well ordered. For example, Guo [1] studied the PBVP for second-order integrodifferential equations of mixed type in real Banach space  :
:

where  ,
,  and
and  are two linear operators,
are two linear operators,  ,
,  are constants. In [1] Guo first obtained a comparison result, and then, by establishing two increasing and decreasing sequences, he proved an existence result for maximal and minimal solutions of the PBVP (1.2) in the ordered interval defined by the lower and upper solutions.
are constants. In [1] Guo first obtained a comparison result, and then, by establishing two increasing and decreasing sequences, he proved an existence result for maximal and minimal solutions of the PBVP (1.2) in the ordered interval defined by the lower and upper solutions.
However, to the best of our knowledge, only in the last few years, it was shown that existence and multiplicity for impulsive differential equation under the condition that the upper solution is not larger than the lower solution, that is, the condition of non-well-ordered upper and lower solutions. In [8], Rach nková and Tvrdý studied the existence of solutions of the nonlinear impulsive periodic boundary value problem
nková and Tvrdý studied the existence of solutions of the nonlinear impulsive periodic boundary value problem

where  ,
,  . Using Leray-Schauder degree, the authors of [8] showed some existence results for (1.3) under the non-well-ordered upper and lower solutions condition. For other results related to non-well-ordered upper and lower solutions, the reader is referred to [7, 9–14]. Also, here we mention the main results of a very recent paper [15]. In that paper, we studied the second-order three-point boundary value problem
. Using Leray-Schauder degree, the authors of [8] showed some existence results for (1.3) under the non-well-ordered upper and lower solutions condition. For other results related to non-well-ordered upper and lower solutions, the reader is referred to [7, 9–14]. Also, here we mention the main results of a very recent paper [15]. In that paper, we studied the second-order three-point boundary value problem

where  ,
,  ,
,  . In [15], we made the following assumption.
. In [15], we made the following assumption.
 There exists
There exists  such that
such that

Let the function  be
be  for
for  . In [15], we proved the following theorem (see, [15, Theorem 3.4]).
. In [15], we proved the following theorem (see, [15, Theorem 3.4]).
Theorem 1.1.
Suppose that  holds,
holds,  and
and  are two strict lower solutions of (1.4),
are two strict lower solutions of (1.4),  and
and  are two strict upper solutions of (1.4), and
are two strict upper solutions of (1.4), and  ,
,  ,
,  ,
,  . Moreover, assume
. Moreover, assume

for some  . Then the three-point boundary value problem (1.4) has at least six solutions
. Then the three-point boundary value problem (1.4) has at least six solutions  .
.
Theorem 1.1 establishes the existence of at least six solutions of the three-point boundary value problem (1.4) only under the condition of two pairs of strict lower and upper solutions. The positions of  and six solutions
and six solutions  in Theorem 1.1 can be illustrated roughly by Figure 1.
in Theorem 1.1 can be illustrated roughly by Figure 1.
In some sense, we can say that these two pairs of lower and upper solutions are parallel to each other. The position of these two pairs of lower and upper solutions is sharply different from that of the lower and upper solutions of the main results in [14, 16, 17]. The technique to prove our main results of [15] is to use the fixed-point index of some increasing operator with respect to some closed convex sets, which are translations of some special cones (see  ,
,  of [15]).
of [15]).
This paper is a continuation of the paper [15]. The aim of this paper is to study the multiplicity of solutions of the impulsive boundary value problem (1.1) under the conditions of non-well-ordered upper and lower solutions. In this paper, we will permit the presence of impulses and the first derivative. The main ideas of this paper are to associate a Leray-Schauder degree with the lower or upper solution. We will give some multiplicity results for at least eight solutions. To obtain this multiplicity result, an additional pair of lower and upper solutions is needed, that is, we will employ a condition of three pairs of lower and upper solutions. The position of these three pairs of lower and upper solutions will be illustrated in Remark 2.16.
2. Results for at Least Eight Solutions
Let  ,
,  is a map from
is a map from  into
into  such that
such that  is continuous at
is continuous at  , left continuous at
, left continuous at  and its right-hand limit
and its right-hand limit  at
at  exits
exits , and
, and  is a map from
is a map from  into
into  such that
such that  and
and  are continuous at
are continuous at  , left continuous at
, left continuous at  and their right-hand limits
and their right-hand limits  and
and  at
at  exits
exits . For each
. For each  , let
, let

where  and
and  . Then,
. Then,  is a real Banach space with the norm
is a real Banach space with the norm  . The function
. The function  is called a solution of the boundary value problem (1.1) if it satisfies all the equalities of (1.1).
is called a solution of the boundary value problem (1.1) if it satisfies all the equalities of (1.1).
Now, for convenience, we make the following assumptions.
 .
.
 is increasing on
is increasing on  .
.
Let  . Now, we define the ordering
. Now, we define the ordering  by
by

Definition 2.1.
The function  is called a strict lower solution of (1.1) if
is called a strict lower solution of (1.1) if

whenever  or
or  for some
for some  and some
and some 

whenever  for each
for each  and
and  ,
,  for each
for each  .
.
The function  is called a strict upper solution of (1.1) if
is called a strict upper solution of (1.1) if

whenever  or
or  for some
for some  and some
and some 

and whenever  for each
for each  and
and  ,
,  for each
for each  .
.
Definition 2.2.
Let  ,
,  for all
for all  . We say that
. We say that  satisfies Nagumo condition with respect to
satisfies Nagumo condition with respect to  if there exists function
if there exists function  such that
such that

Definition 2.3.
Let  be strict upper solutions of (1.1) and
be strict upper solutions of (1.1) and  for each
for each  . Then, we say the upper solutions
. Then, we say the upper solutions  are well ordered if for each
are well ordered if for each  , there exist
, there exist  and
and  small enough such that
small enough such that

Definition 2.4.
Let  be strict lower solutions of (1.1) and
be strict lower solutions of (1.1) and  for each
for each  . Then, we say the lower solutions
. Then, we say the lower solutions  are well ordered if for each
are well ordered if for each  , there exist
, there exist  and
and  small enough such that
small enough such that

From [18, Lemma 5.4.1], we have the following lemma.
Lemma 2.5.
 is a relative compact set if and only if for all
is a relative compact set if and only if for all  ,
,  and
and  are uniformly bounded on
are uniformly bounded on  and equicontinuous on each
and equicontinuous on each  , where
, where  .
.
The following lemma can be easily proved.
Lemma 2.6.
Suppose that  satisfies
satisfies

Then

Lemma 2.7.
Let  and
and  . Then,
. Then,  is a solution of
is a solution of

if and only if  satisfies
satisfies

Proof. .
Let  be a solution of (2.12). From Lemma 2.6, we have
be a solution of (2.12). From Lemma 2.6, we have

Thus,

Using the boundary value condition  , we have
, we have

The equality (2.13) now follows from (2.14) and (2.16).
On the other hand, if  satisfies (2.13), by direct computation, we can easily show that
satisfies (2.13), by direct computation, we can easily show that  satisfies (2.12). The proof is complete.
satisfies (2.12). The proof is complete.
Let us define the operator  by
by

From Lemma 2.5,  is a completely continuous operator.
is a completely continuous operator.
Theorem 2.8.
Suppose that  and
and  hold. Let
hold. Let  be
be  pairs of strict lower and upper solution, and
pairs of strict lower and upper solution, and

Suppose that  ,
,  ,
,  satisfies Nagumo condition with respect to
satisfies Nagumo condition with respect to  . Moreover, the strict lower solutions
. Moreover, the strict lower solutions  and the strict upper solutions
and the strict upper solutions  are well ordered whenever
are well ordered whenever  or
or  for some
for some  and some
and some  . Then, there exist
. Then, there exist  and
and  sufficiently large such that for each
sufficiently large such that for each  and
and 

where

Proof .
We only prove the case when  or
or  for some
for some  and some
and some  . The conclusion is achieved in four steps.
. The conclusion is achieved in four steps.
Step 1.
Since  satisfies Nagumo condition with respect to
satisfies Nagumo condition with respect to  , then there exists
, then there exists  such that
such that

Let  . Take
. Take  such that
such that

and  such that
such that

Let  . Define the functions
. Define the functions  by
by

For each  , let us define the functions
, let us define the functions  by
by

It is easy to see that there exists  such that
such that

Let us define the operator  by
by

By (2.26), we have

From (2.28), we have  for each
for each  . Let
. Let  . Then,
. Then,  . By the properties of the Leray-Schauder degree, we have
. By the properties of the Leray-Schauder degree, we have

Thus,  has at least one fixed point
has at least one fixed point  . From Lemma 2.7,
. From Lemma 2.7,  satisfies
satisfies

Step 2.
Next, we will show that


We first show that

To begin, we show that  for all
for all  . Suppose not, then there exists
. Suppose not, then there exists  such that
such that  . Set
. Set  for
for  . There are a number of cases to consider.
. There are a number of cases to consider.
-
(1)
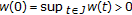 , then, we have
, then, we have 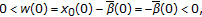 (2.34)
(2.34)
which is a contradiction.
-
(2)
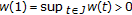 ; assume without loss of generality that
; assume without loss of generality that  and
and  for some
for some 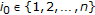 , then, we have
, then, we have 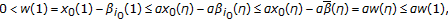 (2.35)
(2.35)
which is a contradiction.
-
(3)
There exist
 and
and  such that
such that  . Assume without loss of generality that
. Assume without loss of generality that  for some
for some 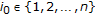 . We have the following two cases:
. We have the following two cases:
(3A)  for each
for each  and
and  ;
;
(3B) there exists  such that
such that  .
.
For case (3A), there exists  small enough such that
small enough such that  and
and

Then,  ,
,  is the maximum of
is the maximum of  on
on  . Thus,
. Thus,  . By (2.30), we have
. By (2.30), we have

which is a contradiction.
For case (3B), set  for
for  . For any
. For any  , we have
, we have

This implies that  is a local maximum. Since
is a local maximum. Since  , then
, then  ,
,  . Therefore,
. Therefore,

which is a contradiction.
-
(4)
There exists
 such that
such that 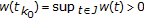 . Without loss of generality, we may assume
. Without loss of generality, we may assume 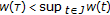 for each
for each  and
and 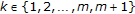 . (Otherwise, if there exists
. (Otherwise, if there exists  for some
for some 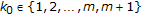 such that
such that 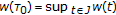 , then we can get a contradiction as in case (3)). In this case, we have the following two subcases:
, then we can get a contradiction as in case (3)). In this case, we have the following two subcases:
(4A) there exists  such that
such that  for
for  and
and  ;
;
(4B) there exists a subset  such that
such that

while  for each
for each  .
.
First, we consider case (4A). Since  is increasing on
is increasing on  , then
, then

Then, there exists  small enough such that
small enough such that  for
for  and so
and so  for
for  . Since
. Since  is a strict upper solution, we have
is a strict upper solution, we have

Since  for each
for each  , then we have
, then we have  . Similarly, we have
. Similarly, we have  . Therefore,
. Therefore,

which is contradiction.
Now we consider case (4B). Since  is increasing, then we have
is increasing, then we have

while  for each
for each  . For case (4B), we have two subcases:
. For case (4B), we have two subcases:
(4Ba) there exists  small enough and
small enough and  such that
such that  for
for  ;
;
(4Bb) there exists  small enough and
small enough and  ,
,  such that
such that

For case (4Ba) as in case (4A), we can easily obtain a contradiction. For case (4Bb), we have

In the same way as in the proof of case (4A), we see that  ,
,  and we have
and we have  . Note that
. Note that  , and we have
, and we have

which is a contradiction.
-
(5)
There exists a
 such that
such that  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  for each
for each 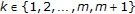 and
and 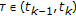 . We have two subcases:
. We have two subcases:
(5A) there exists  such that
such that  for each
for each  ;
;
(5B) there exists a subset  such that
such that

while  for each
for each  .
.
Since  is increasing, then for case (5A), we have
is increasing, then for case (5A), we have

and for case (5B), we have  and
and

while  for each
for each  . Therefore, we can use the same method as in case (4) to obtain a contradiction.
. Therefore, we can use the same method as in case (4) to obtain a contradiction.
From the discussions of (1)–(5), we see that  for
for  . Similarly, we can prove that
. Similarly, we can prove that  for
for  . Thus, (2.33) holds.
. Thus, (2.33) holds.
Next, we prove that  . If the inequality
. If the inequality  does not hold, then either there exists
does not hold, then either there exists  such that
such that  or there exists
or there exists  such that
such that  . Set
. Set  for
for  . Then, we have either
. Then, we have either  or
or  for some
for some  . Essentially the same reasoning as in (1)–(5) above yields a contradiction. Thus,
. Essentially the same reasoning as in (1)–(5) above yields a contradiction. Thus,  . Similarly,
. Similarly,  . Consequently, (2.31) holds.
. Consequently, (2.31) holds.
Step 3.
Now, we show (2.32). Suppose not, then we have the following two subcases:
(I)there exists  such that
such that  ;
;
(II)there exists  such that
such that  .
.
We only consider case (II). A similar argument works for case (I). We may assume without loss of generality that  . By the mean-value theorem, there exists
. By the mean-value theorem, there exists  such that
such that

Let  be such that
be such that  , then, there exist??
, then, there exist?? such that
such that  ,
,  ,
,  , and
, and  for
for  . Therefore,
. Therefore,

Consequently,

On the other hand,

which is a contradiction. Thus, (2.32) holds.
Step 4.
From the excision property of Leray-Schauder degree and (2.29), we have

From (2.31) and (2.32), we see that  for each
for each  , and so
, and so

The proof is complete.
Remark 2.9.
From the proof of Theorem 2.8, we see that  has no fixed point on
has no fixed point on 
Theorem 2.10.
Suppose that  ,
,  hold,
hold,  are strict lower solutions,
are strict lower solutions,  are strict upper solutions,
are strict upper solutions,  ,
,  ,
,  for some
for some  , and??
, and?? satisfies Nagumo condition with respect to
satisfies Nagumo condition with respect to  . Moreover, the strict lower solutions
. Moreover, the strict lower solutions  are well ordered whenever
are well ordered whenever  or
or  for some
for some  and some
and some  . Then, (1.1) has at least three solutions
. Then, (1.1) has at least three solutions  , and
, and  , such that
, such that

and  for some
for some  .
.
Proof .
Set  for
for  , and
, and  for each
for each  . From Theorem 2.8, we see that there exist
. From Theorem 2.8, we see that there exist  and
and  large enough such that
large enough such that

where  ,
,  , and
, and  . Then,
. Then,  has fixed points
has fixed points  and
and  , respectively. From the conditions of Theorem 2.10, we see that
, respectively. From the conditions of Theorem 2.10, we see that  . Let
. Let  be a continuous function on
be a continuous function on  such that its graph passes the points
such that its graph passes the points  and
and  , and satisfies
, and satisfies  . By the well-known Weierstrass approximation theorem, there exists
. By the well-known Weierstrass approximation theorem, there exists  such that
such that

It is easy to see that  , and so
, and so  is a nonempty open set. Note
is a nonempty open set. Note  has no fixed point on
has no fixed point on  , and
, and  . From (2.58), we have
. From (2.58), we have

Thus,  has at least one fixed point
has at least one fixed point  . Since
. Since  , then there exist
, then there exist  such that
such that  and
and  . The proof is complete.
. The proof is complete.
Remark 2.11.
Theorem 2.10 is a partial generalization of the main results of [16, Theorem 2.2]. Here, we do not need to assume that  satisfies
satisfies  .
.
Remark 2.12.
The position of  in Theorem 2.10 can be illustrated roughly by Figure 2.
in Theorem 2.10 can be illustrated roughly by Figure 2.
Remark 2.13.
The relationship of  is different from that of [12, Theorems 9 and 10].
is different from that of [12, Theorems 9 and 10].
Similarly, we have the following result.
Theorem 2.14.
Suppose that  ,
,  hold,
hold,  are strict lower solutions of (1.1),
are strict lower solutions of (1.1),  and
and  are strict upper solutions of (1.1),
are strict upper solutions of (1.1),  ,
,  ,
,  for some
for some  , and??
, and?? satisfies Nagumo condition with respect to
satisfies Nagumo condition with respect to  . Moreover, the strict upper solutions
. Moreover, the strict upper solutions  are well ordered whenever
are well ordered whenever  or
or  for some
for some  and some
and some  . Then, (1.1) has at least three solutions
. Then, (1.1) has at least three solutions  such that
such that

and  for some
for some  .
.
From Theorems 2.10 and 2.14, we have the following Theorem 2.15.
Theorem 2.15.
Suppose that  ,
,  hold,
hold,  are three strict lower solutions of (1.1),
are three strict lower solutions of (1.1),  are three strict upper solutions of (1.1),
are three strict upper solutions of (1.1),  ,
,  ,
,  for some
for some  , and??
, and?? satisfies Nagumo conditions with respect to
satisfies Nagumo conditions with respect to  . Moreover, the strict lower solutions
. Moreover, the strict lower solutions  and the strict upper solutions
and the strict upper solutions  are well ordered whenever
are well ordered whenever  or
or  for some
for some  and some
and some  . Then, (1.1) has at least eight solutions.
. Then, (1.1) has at least eight solutions.
Proof .
Now Theorem 2.10 guarantees that (1.1) has at least three solutions  such that
such that

and  for some
for some  .
.
Also (1.1) has at least two solutions  and
and  such that
such that

and  .
.
Now Theorem 2.14 guarantees that (1.1) has at least two solutions  such that
such that

and  .
.
Also (1.1) has at least one solution  such that
such that  and
and  for some
for some  . It is easy to see that
. It is easy to see that  are distinct eight solutions of (1.1). The proof is complete.
are distinct eight solutions of (1.1). The proof is complete.
Remark 2.16.
The position of  in Theorem 2.15 can be illustrated roughly by Figure 3.
in Theorem 2.15 can be illustrated roughly by Figure 3.
3. Further Discussions
For simplicity, in this section, we will always assume that

In this case, (1.1) can be reduced to the following three-point boundary value problem

where  and
and  .
.
In this section, we will use the following assumptions.
 Suppose that
Suppose that  are two strict lower solutions,
are two strict lower solutions,  are two strict upper solutions of (1.1),
are two strict upper solutions of (1.1),  ,
,  , and
, and  for some
for some  .
.
Recently, this multipoint boundary value problem has been studied by many authors, see [16, 17, 19–21] and the references therein. The goal of this section is to prove some multiplicity results for (3.2) using the condition of two pairs of strict upper and lower solutions. As we can see from [13], some bounding condition on the nonlinear term is needed. Instead of the space  , in this section we will use the space
, in this section we will use the space  . First, we have the following theorem.
. First, we have the following theorem.
Theorem 3.1.
Suppose that  holds, and
holds, and

for some  . Then, (3.2) has at least eight solutions.
. Then, (3.2) has at least eight solutions.
Proof .
First, we show that there exist strict lower and upper solutions  such that
such that

Let  . Now, we consider the following boundary value problem:
. Now, we consider the following boundary value problem:

Let

By Lemma 2.7, we have

It is easy to see that  and
and  for each
for each  . Thus,
. Thus,  for each
for each  , and therefore,
, and therefore,  ,
,  for
for  . On the other hand, from (3.5), it is easy to see that
. On the other hand, from (3.5), it is easy to see that  is a strict upper solution of (1.1). Similarly, we can show the existence of
is a strict upper solution of (1.1). Similarly, we can show the existence of  . Then, by Theorem 2.15, the conclusion holds.
. Then, by Theorem 2.15, the conclusion holds.
Remark 3.2.
Obviously, the condition (3.3) is restrictive. In the following, we will make use of a weaker condition. We study the multiplicity of solutions of (3.2) under a Nagumo-Knobloch-Schmitt condition. For this kind of bounding condition, the reader is referred to [13].
Theorem 3.3.
Suppose  holds, and there exists function
holds, and there exists function  such that
such that



where  ,
,  ,
,

Then, (3.2) has at least eight solutions.
Proof .
Let  for each
for each  , and
, and

Now, we consider the following boundary value problem:

From  and (3.8), we see that
and (3.8), we see that  are strict lower solutions of (3.13), and
are strict lower solutions of (3.13), and  and
and  are two strict upper solutions of (3.13). By Theorem 3.1, (3.13) has at least eight solutions
are two strict upper solutions of (3.13). By Theorem 3.1, (3.13) has at least eight solutions  . We need only to show that
. We need only to show that  are solutions of (3.2). We claim that
are solutions of (3.2). We claim that

We only show that  for
for  . If
. If  for some
for some  , then
, then  for some
for some  , where
, where  for
for  . If
. If  , then
, then  , and so
, and so

which contradicts (3.9).
From Lemma 2.6, we have

and so

This implies that  . Therefore, (3.14) holds. Integrating (3.14), we have
. Therefore, (3.14) holds. Integrating (3.14), we have

From (3.13)–(3.18), we see that  are eight solutions of (3.2). The proof is complete.
are eight solutions of (3.2). The proof is complete.
Remark 3.4.
We also can replace (3.3) by other bounding conditions, see [13].
Remark 3.5.
To end this paper, we point out that the results of this paper can be applied to study the multiplicity of radial solutions of elliptic differential equation in an annulus with impulses at some radii.
References
Guo D: Periodic boundary value problems for second order impulsive integro-differential equations in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 1997,28(6):983-997. 10.1016/S0362-546X(97)82855-6
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Guo D:Multiple positive solutions of a boundary value problem for
 th-order impulsive integro-differential equations in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2004,56(7):985-1006. 10.1016/j.na.2003.10.023
th-order impulsive integro-differential equations in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2004,56(7):985-1006. 10.1016/j.na.2003.10.023Erbe LH, Liu X: Quasi-solutions of nonlinear impulsive equations in abstract cones. Applicable Analysis 1989,34(3-4):231-250. 10.1080/00036818908839897
Liu X: Nonlinear boundary value problems for first order impulsive integro-differential equations. Applicable Analysis 1990,36(1-2):119-130. 10.1080/00036819008839925
Picard E: Sur l'application des méthodes d'approximations successives à l' étude de certaines équations différentielles ordinaries. Journal de Mathématiques Pures et Appliquées 1893, 9: 217-271.
De Coster C, Habets P: An overview of the method of lower and upper solutions for ODEs. In Nonlinear Analysis and Its Applications to Differential Equations. Volume 43. Birkhauser, Boston, Mass, USA; 2001:3-22.
Rachunková I, Tvrdý M: Non-ordered lower and upper functions in second order impulsive periodic problems. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2005,12(3-4):397-415.
Amann H, Ambrosetti A, Mancini G: Elliptic equations with noninvertible Fredholm linear part and bounded nonlinearities. Mathematische Zeitschrift 1978,158(2):179-194. 10.1007/BF01320867
De Coster C, Henrard M: Existence and localization of solution for second order elliptic BVP in presence of lower and upper solutions without any order. Journal of Differential Equations 1998,145(2):420-452. 10.1006/jdeq.1998.3423
Rachunková I, Tvrdý M:Periodic problems with
 -Laplacian involving non-ordered lower and upper functions. Fixed Point Theory 2005,6(1):99-112.
-Laplacian involving non-ordered lower and upper functions. Fixed Point Theory 2005,6(1):99-112.Rachunková I: Upper and lower solutions and topological degree. Journal of Mathematical Analysis and Applications 1999,234(1):311-327. 10.1006/jmaa.1999.6375
Rachunková I: Upper and lower solutions and multiplicity results. Journal of Mathematical Analysis and Applications 2000,246(2):446-464. 10.1006/jmaa.2000.6798
Habets P, Omari P: Existence and localization of solutions of second order elliptic problems using lower and upper solutions in the reversed order. Topological Methods in Nonlinear Analysis 1996,8(1):25-56.
Xu X, O'Regan D, Sun J: Multiplicity results for three-point boundary value problems with a non-well-ordered upper and lower solution condition. Mathematical and Computer Modelling 2007,45(1-2):189-200. 10.1016/j.mcm.2006.05.003
Khan RA, Webb JRL: Existence of at least three solutions of a second-order three-point boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2006,64(6):1356-1366. 10.1016/j.na.2005.06.040
Xian X: Three solutions for three-point boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2005,62(6):1053-1066. 10.1016/j.na.2005.04.017
Guo D, Sun J, Liu Z: The Funtional Method for Nonlinear Ordinary Differential Equations. Shandong Science and Technology Press, Jinan, China; 1995.
Liu B: Positive solutions of second-order three-point boundary value problems with change of sign. Computers & Mathematics with Applications 2004,47(8-9):1351-1361. 10.1016/S0898-1221(04)90128-9
Gupta CP, Trofimchuk SI: Existence of a solution of a three-point boundary value problem and the spectral radius of a related linear operator. Nonlinear Analysis: Theory, Methods & Applications 1998,34(4):489-507. 10.1016/S0362-546X(97)00584-1
Ma R, Castaneda N:Existence of solutions of nonlinear
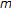 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
Acknowledgments
This paper is supported by Natural Science Foundation of Jiangsu Education Committee (04KJB110138) and China Postdoctoral Science Foundation (2005037712).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xian, X., O'Regan, D. & Agarwal, R. Multiplicity Results via Topological Degree for Impulsive Boundary Value Problems under Non-Well-Ordered Upper and Lower Solution Conditions. Bound Value Probl 2008, 197205 (2008). https://doi.org/10.1155/2008/197205
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/197205

 and six solutions
and six solutions  in Theorem 1. 1.
in Theorem 1. 1.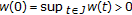 , then, we have
, then, we have 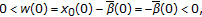
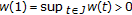 ; assume without loss of generality that
; assume without loss of generality that 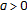 and
and  for some
for some 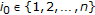 , then, we have
, then, we have 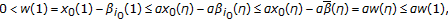
 and
and  such that
such that  . Assume without loss of generality that
. Assume without loss of generality that  for some
for some 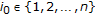 . We have the following two cases:
. We have the following two cases: such that
such that 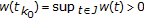 . Without loss of generality, we may assume
. Without loss of generality, we may assume 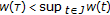 for each
for each  and
and 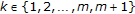 . (Otherwise, if there exists
. (Otherwise, if there exists  for some
for some 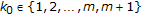 such that
such that 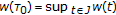 , then we can get a contradiction as in case (3)). In this case, we have the following two subcases:
, then we can get a contradiction as in case (3)). In this case, we have the following two subcases: such that
such that  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  for each
for each 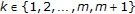 and
and 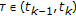 . We have two subcases:
. We have two subcases:
 in Theorem 2. 10.
in Theorem 2. 10.
 in Theorem 2. 15.
in Theorem 2. 15. th-order impulsive integro-differential equations in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2004,56(7):985-1006. 10.1016/j.na.2003.10.023
th-order impulsive integro-differential equations in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2004,56(7):985-1006. 10.1016/j.na.2003.10.023 -Laplacian involving non-ordered lower and upper functions. Fixed Point Theory 2005,6(1):99-112.
-Laplacian involving non-ordered lower and upper functions. Fixed Point Theory 2005,6(1):99-112.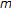 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320