- Research Article
- Open access
- Published:
Existence Result for a Class of Elliptic Systems with Indefinite Weights in 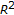
Boundary Value Problems volume 2008, Article number: 217636 (2008)
Abstract
We obtain the existence of a nontrivial solution for a class of subcritical elliptic systems with indefinite weights in  . The proofs base on Trudinger-Moser inequality and a generalized linking theorem introduced by Kryszewski and Szulkin.
. The proofs base on Trudinger-Moser inequality and a generalized linking theorem introduced by Kryszewski and Szulkin.
1. Introduction
In this paper, we study the existence of a nontrivial solution for the following systems of two semilinear coupled Poisson equations

where  and
and  are continuous functions on
are continuous functions on  and have the maximal growth on
and have the maximal growth on  which allows to treat problem (P) variationally,
which allows to treat problem (P) variationally,  is the Laplace operator.
is the Laplace operator.
Recently, there exists an extensive bibliography in the study of elliptic problem in  [1–6]. As dimensions
[1–6]. As dimensions  in 1998, de Figueiredo and Yang [5] considered the following coupled elliptic systems:
in 1998, de Figueiredo and Yang [5] considered the following coupled elliptic systems:

where  are radially symmetric in
are radially symmetric in  and satisfied the following Ambrosetti-Rabinowitz condition:
and satisfied the following Ambrosetti-Rabinowitz condition:

and for some  . They obtained the decay, symmetry, and existence of solutions for problem (1.2). In 2004, Li and Yang [6] proved that problem (1.2) possesses at least a positive solution when the nonlinearities
. They obtained the decay, symmetry, and existence of solutions for problem (1.2). In 2004, Li and Yang [6] proved that problem (1.2) possesses at least a positive solution when the nonlinearities  and
and  are "asymptotically linear" at infinity and "superlinear" at zero, that is,
are "asymptotically linear" at infinity and "superlinear" at zero, that is,
(1) uniformly in
uniformly in 
(2) uniformly with respect to
uniformly with respect to 
In 2006, Colin and Frigon [1] studied the following systems of coupled Poission equations with critical growth in unbounded domains:

where  is critical Sobolev exponent,
is critical Sobolev exponent, 
 and
and  with
with  for a domain containing the origin
for a domain containing the origin  Here,
Here,  denotes the open ball centered at the origin of radius
denotes the open ball centered at the origin of radius  . The existence of a nontrivial solution was obtained by using a generalized linking theorem.
. The existence of a nontrivial solution was obtained by using a generalized linking theorem.
As it is well known in dimensions  the nonlinearities are required to have polynomial growth at infinity, so that one can define associated functionals in Sobolev spaces. Coming to dimension
the nonlinearities are required to have polynomial growth at infinity, so that one can define associated functionals in Sobolev spaces. Coming to dimension  much faster growth is allowed for the nonlinearity. In fact, the Trudinger-Moser estimates in
much faster growth is allowed for the nonlinearity. In fact, the Trudinger-Moser estimates in  replace the Sobolev embedding theorem used in
replace the Sobolev embedding theorem used in 
In dimension  Adimurth and Yadava [7], de Figueiredo et al. [8] discussed the solvability of problems of the type
Adimurth and Yadava [7], de Figueiredo et al. [8] discussed the solvability of problems of the type

where  is some bounded domain in
is some bounded domain in  Shen et al. [9] considered the following nonlinear elliptic problems with critical potential:
Shen et al. [9] considered the following nonlinear elliptic problems with critical potential:

and obtained some existence results. In the whole space  some authors considered the following single semilinear elliptic equations:
some authors considered the following single semilinear elliptic equations:

As the potential  and the nonlinearity
and the nonlinearity  are asymptotic to a constant function, Cao [10] obtained the existence of a nontrivial solution. As the potential
are asymptotic to a constant function, Cao [10] obtained the existence of a nontrivial solution. As the potential  and the nonlinearity
and the nonlinearity  are asymptotically periodic at infinity, Alves et al. [11] proved the existence of at least one positive weak solution.
are asymptotically periodic at infinity, Alves et al. [11] proved the existence of at least one positive weak solution.
Our aim in this paper is to establish the existence of a nontrivial solution for problem (P) in subcritical case. To our knowledge, there are no results in the literature establishing the existence of solutions to these problems in the whole space. However, it contains a basic difficulty. Namely, the energy functional associated with problem (P) has strong indefinite quadratic part, so there is not any more mountain pass structure but linking one. Therefore, the proofs of our main results cannot rely on classical min-max results. Combining a generalized linking theorem introduced by Kryszewski and Szulkin [12] and Trudinger-Moser inequality, we prove an existence result for problem (P).
The paper is organized as follows. In Section 2, we recall some results and state our main results. In Section 3, main result is proved.
2. Preliminaries and Main Results
Consider the Hilbert space [13]

and denote the product space  endowed with the inner product:
endowed with the inner product:

If we define

It is easy to check that  since
since

Let us denote by  (resp.,
(resp.,  ) the projection of
) the projection of  on to
on to  (resp.,
(resp.,  ), we have
), we have

Now, we define the functional

where

Let  and let
and let  we define
we define

Here, we assume the following condition:
(H1) 
(H2)  uniformly with respect to
uniformly with respect to 
(H3) there exist  and
and  such that
such that

Assume (H1), (H2), and (H3), and suppose
(1) where
where  is sequentially lower semicontinu- ous, bounded below, and
is sequentially lower semicontinu- ous, bounded below, and  is weakly sequentially continuous;
is weakly sequentially continuous;
(2)there exist  , and
, and  , such that
, such that

Then, there exist  and a sequence
and a sequence  such that
such that

Moreover, 
Theorem 2.2.
Under the assumptions (H1), (H2), and (H3), if  and
and  has subcritical growth (see definition below), problem (P) possesses a nontrivial weak solution.
has subcritical growth (see definition below), problem (P) possesses a nontrivial weak solution.
In the whole space  do Ó and Souto [15] proved a version of Trudinger-Moser inequality, that is,
do Ó and Souto [15] proved a version of Trudinger-Moser inequality, that is,
(i)if  , we have
, we have

(ii)if  and
and  then there exists a constant
then there exists a constant  such that
such that

Deffinition.
We say has subcritical growth at  if for all
if for all  there exists a positive constant
there exists a positive constant  such that
such that

3. Proof of Theorem 2.2
In this section, we will prove Theorem 2.2. under our assumptions and (2.14), there exist  such that
such that

Then, we obtain

Therefore, the functional  is well defined. Furthermore, using standard arguments, we obtain the functional
is well defined. Furthermore, using standard arguments, we obtain the functional  is
is  functional in
functional in  and
and

Consequently, the weak solutions of problem (P) are exactly the critical points of  in
in  Now, we prove that the functional
Now, we prove that the functional  satisfied the geometry of Lemma 2.1.
satisfied the geometry of Lemma 2.1.
Lemma 3.1.
There exist  and
and  such that
such that 
Proof.
By (2.14) and assumption (H2), there exists  such that
such that

and thus on  we have
we have

So, by the Sobolev embedding theorem and (2.12), we can choose  sufficiently small, such that
sufficiently small, such that

Lemma 3.2.
There exist  and
and  such that
such that 
Proof.
-
(1)
By assumption (H3), we have on

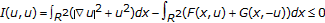 (3.7)
(3.7)
because  for any
for any 
-
(2)
Assumption (H3) implies that there exist
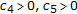 such that
such that  (3.8)
(3.8)
Now, we choose  such that
such that  , then
, then

Because  it follows that for
it follows that for 

and so, taking  large, we get
large, we get 
Proof of Theorem 2.2.
By Lemma 3.1, there exist  and
and  such that
such that  By Lemma 3.2, there exist
By Lemma 3.2, there exist  and
and  such that
such that  Since
Since  , we have
, we have

From (2.14), (3.1), and assumption (H3),  and
and  is sequentially lower semicontinuous by
is sequentially lower semicontinuous by  and Fatou's lemma;
and Fatou's lemma;  is weakly sequentially continuous. Thus, by Lemma 2.1
is weakly sequentially continuous. Thus, by Lemma 2.1 there exists a sequence
there exists a sequence  such that
such that

Claim 3.3.
There is  such that
such that  for any
for any  Indeed, from (3.12), we obtain that the sequence
Indeed, from (3.12), we obtain that the sequence  satisfies
satisfies

where  as
as  Taking
Taking  in (3.13) and assumption (H3), we have
in (3.13) and assumption (H3), we have

where  depends only on
depends only on  and
and  in assumption (H3). Since
in assumption (H3). Since  we have
we have  and thus
and thus

On the other hand, let  in (3.13), we obtain
in (3.13), we obtain

that is,

Now, we recall the following inequality (see [7, Lemma 2.4]):

Let  and
and  where
where  is defined in (2.14), we have
is defined in (2.14), we have

By (2.12), we have  By (2.14), we have
By (2.14), we have

Hence, we have

for some positive constant  So we have
So we have

Using a similar argument, we obtain

for some positive constant  Combining (3.22) and (3.23), we have
Combining (3.22) and (3.23), we have

for some positive constant  which implies that
which implies that  . Thus, for a subsequence still denoted by
. Thus, for a subsequence still denoted by  there is
there is  such that
such that

Then, there exists  such that
such that  From (2.12) and (2.14), we have
From (2.12) and (2.14), we have  this implies
this implies

Similarly, we can obtain

From these, we have  , so
, so  is weak solution of problem (P).
is weak solution of problem (P).
Claim 3.4.
 is nontrivial. By contradiction, since
is nontrivial. By contradiction, since  has subcritical growth, from (2.14) and Hölder inequality, we have
has subcritical growth, from (2.14) and Hölder inequality, we have

where  Choosing suitable
Choosing suitable  and
and  we have
we have

Then, we obtain

Since  in
in  as
as  this will lead to
this will lead to

Similarly, we have

Using assumption (H3), we obtain

This together with  we have
we have

Thus, we see that

which is a contradiction to  as
as 
Consequently, we have a nontrivial critical point of the functional  and conclude the proof of Theorem 2.2.
and conclude the proof of Theorem 2.2.
References
Colin F, Frigon M: Systems of coupled Poisson equations with critical growth in unbounded domains. Nonlinear Differential Equations and Applications 2006,13(3):369-384. 10.1007/s00030-006-4012-1
Ding Y, Li S: Existence of entire solutions for some elliptic systems. Bulletin of the Australian Mathematical Society 1994,50(3):501-519. 10.1017/S0004972700013605
de Figueiredo DG: Nonlinear elliptic systems. Anais da Academia Brasileira de Ciências 2000,72(4):453-469. 10.1590/S0001-37652000000400002
de Figueiredo DG, do Ó JM, Ruf B: Critical and subcritical elliptic systems in dimension two. Indiana University Mathematics Journal 2004,53(4):1037-1054. 10.1512/iumj.2004.53.2402
de Figueiredo DG, Yang J: Decay, symmetry and existence of solutions of semilinear elliptic systems. Nonlinear Analysis: Theory, Methods & Applications 1998,33(3):211-234. 10.1016/S0362-546X(97)00548-8
Li G, Yang J: Asymptotically linear elliptic systems. Communications in Partial Differential Equations 2004,29(5-6):925-954.
Adimurthi , Yadava SL:Multiplicity results for semilinear elliptic equations in a bounded domain of
 involving critical exponents. Annali della Scuola Normale Superiore di Pisa 1990,17(4):481-504.
involving critical exponents. Annali della Scuola Normale Superiore di Pisa 1990,17(4):481-504.de Figueiredo DG, Miyagaki OH, Ruf B:Elliptic equations in
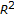 with nonlinearities in the critical growth range. Calculus of Variations and Partial Differential Equations 1995,3(2):139-153. 10.1007/BF01205003
with nonlinearities in the critical growth range. Calculus of Variations and Partial Differential Equations 1995,3(2):139-153. 10.1007/BF01205003Shen Y, Yao Y, Chen Z:On a class of nonlinear elliptic problem with critical potential in
 . Science in China Series A 2004, 34: 610-624.
. Science in China Series A 2004, 34: 610-624.Cao DM:Nontrivial solution of semilinear elliptic equation with critical exponent in
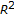 . Communications in Partial Differential Equations 1992,17(3-4):407-435. 10.1080/03605309208820848
. Communications in Partial Differential Equations 1992,17(3-4):407-435. 10.1080/03605309208820848Alves CO, do Ó JM, Miyagaki OH:On nonlinear perturbations of a periodic elliptic problem in
 involving critical growth. Nonlinear Analysis: Theory, Methods & Applications 2004,56(5):781-791. 10.1016/j.na.2003.06.003
involving critical growth. Nonlinear Analysis: Theory, Methods & Applications 2004,56(5):781-791. 10.1016/j.na.2003.06.003Kryszewski W, Szulkin A: Generalized linking theorem with an application to a semilinear Schrödinger equation. Advances in Differential Equations 1998,3(3):441-472.
Willem M: Minimax Theorems, Progress in Nonlinear Differential Equations and Their Applications. Volume 24. Birkhäuser, Boston, Mass, USA; 1996:x+162.
Li G, Szulkin A: An asymptotically periodic Schrödinger equation with indefinite linear part. Communications in Contemporary Mathematics 2002,4(4):763-776. 10.1142/S0219199702000853
do Ó JM, Souto MAS:On a class of nonlinear Schrödinger equations in
 involving critical growth. Journal of Differential Equations 2001,174(2):289-311. 10.1006/jdeq.2000.3946
involving critical growth. Journal of Differential Equations 2001,174(2):289-311. 10.1006/jdeq.2000.3946
Acknowledgment
This work is supported by Innovation Program of Shanghai Municipal Education Commission under Grant no. 08 YZ93.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, G., Liu, S. Existence Result for a Class of Elliptic Systems with Indefinite Weights in 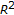 .
Bound Value Probl 2008, 217636 (2008). https://doi.org/10.1155/2008/217636
.
Bound Value Probl 2008, 217636 (2008). https://doi.org/10.1155/2008/217636
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/217636

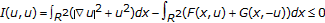
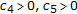 such that
such that 
 involving critical exponents. Annali della Scuola Normale Superiore di Pisa 1990,17(4):481-504.
involving critical exponents. Annali della Scuola Normale Superiore di Pisa 1990,17(4):481-504.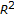 with nonlinearities in the critical growth range. Calculus of Variations and Partial Differential Equations 1995,3(2):139-153. 10.1007/BF01205003
with nonlinearities in the critical growth range. Calculus of Variations and Partial Differential Equations 1995,3(2):139-153. 10.1007/BF01205003 . Science in China Series A 2004, 34: 610-624.
. Science in China Series A 2004, 34: 610-624.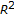 . Communications in Partial Differential Equations 1992,17(3-4):407-435. 10.1080/03605309208820848
. Communications in Partial Differential Equations 1992,17(3-4):407-435. 10.1080/03605309208820848 involving critical growth. Nonlinear Analysis: Theory, Methods & Applications 2004,56(5):781-791. 10.1016/j.na.2003.06.003
involving critical growth. Nonlinear Analysis: Theory, Methods & Applications 2004,56(5):781-791. 10.1016/j.na.2003.06.003 involving critical growth. Journal of Differential Equations 2001,174(2):289-311. 10.1006/jdeq.2000.3946
involving critical growth. Journal of Differential Equations 2001,174(2):289-311. 10.1006/jdeq.2000.3946