- Research Article
- Open access
- Published:
Multiple Nodal Solutions for Some Fourth-Order Boundary Value Problems via Admissible Invariant Sets
Boundary Value Problems volume 2008, Article number: 403761 (2008)
Abstract
Existence and multiplicity results for nodal solutions are obtained for the fourth-order boundary value problem (BVP)  ,
,  ,
,  , where
, where  is continuous. The critical point theory and admissible invariant sets are employed to discuss this problem.
is continuous. The critical point theory and admissible invariant sets are employed to discuss this problem.
1. Introduction
In this paper, we consider the existence of nodal solutions to the semilinear fourth-order equation:


where  is continuous.
is continuous.
Owning to the importance of higher-order differential equations in physics, the existence and multiplicity of the solutions to such problems have been studied by many authors. They obtained the existence of solutions by the cone expansion or compression fixed point theorem [1–6]; sub-sup solution method [7–9]; critical point theory [10–13]; Morse theory [14, 15]; and eta [16, 17]. There are also papers which study nodal solutions for elliptic equations [18, 19]. In particular, in [20], Han and Li obtained multiple positive, negative, and sign-changing solutions by combining the critical point theory and the method of sub-sup solutions for the (BVP) (1.2). The main result is as follows:
 there exist a strict subsolution
there exist a strict subsolution  and a strict supersolution
and a strict supersolution  of (BVP) (1.2) with
of (BVP) (1.2) with  ,
,  , and
, and  ;
;
 is strictly increasing in
is strictly increasing in  ;
;
 is locally Lipschitz continuous in
is locally Lipschitz continuous in  ;
;
 there exist
there exist  and
and  such that
such that  for all
for all  and
and 
Theorem 1.1 (see [20]).
Assume that  hold. Then, (BVP) (1.2) has at least four solutions.
hold. Then, (BVP) (1.2) has at least four solutions.
Motivated by their ideas, we cannot help wondering if there are no strict subsolution and supersolution of (BVP) (1.2), can we still get the nodal solutions just by critical point theory? In this paper, we will use the admissible invariant sets and critical point theory to settle this problem. But we should point out that in all theorems of our paper, the nonlinearity  is assumed to be odd in
is assumed to be odd in  , while no such symmetry is required in [20].
, while no such symmetry is required in [20].
The paper is organized as follows: in Section 2, we give some preliminaries, including the critical point theorems which will be used in our main results and some concepts concerning the partially ordered Banach space. The main results and proofs are established in Section 3.
2. Preliminaries
Let  be a Hilbert space and
be a Hilbert space and  a Banach space densely embedded in
a Banach space densely embedded in  . Assume that
. Assume that  has a closed convex cone
has a closed convex cone  and that
and that  has interior points in
has interior points in  , that is,
, that is,  with
with  the interior and
the interior and  the boundary of
the boundary of  in
in  .
.
Let  and
and  for
for  . We use the following notation:
. We use the following notation:  ,
,  ,
,  ,
,  for
for  . Let
. Let  and
and  denote the norms in
denote the norms in  and
and  , respectively.
, respectively.
Lemma 2.1 (see [21]).
Assume  is a Hilbert space, and
is a Hilbert space, and  is a closed convex set of
is a closed convex set of  ,
,  , and
, and  . Then, there exists a pseudogradient vector field
. Then, there exists a pseudogradient vector field  for
for  , and
, and  . Furthermore, if
. Furthermore, if  is even,
is even,  , then
, then  is odd.
is odd.
Consider the pseudogradient flow  on
on  associated with the vector field
associated with the vector field  ,
,

We see that  is odd in
is odd in  , if
, if  is odd in
is odd in  . Since
. Since  for
for  and
and  the Brezis-Martin theorem [22] implies that
the Brezis-Martin theorem [22] implies that  for
for  .
.
Definition 2.2 (see [21, 23]).
With the flow  , a subset
, a subset  is called an invariant set if
is called an invariant set if  for
for  .
.
Let us assume that
(F) ,
,  for
for  ,
,  is continuous.
is continuous.
Under condition  , we have
, we have  for
for  and
and  is continuous in
is continuous in  .
.
Definition 2.3 (see [21]).
Let  be an invariant set under
be an invariant set under  .
.  is said to be an admissible invariant set for
is said to be an admissible invariant set for  if (a)
if (a)  is the closure of an open set in
is the closure of an open set in  , that is,
, that is,  ; (b) if
; (b) if  for some
for some  and
and  in
in  as
as  for some
for some  , then
, then  in
in  ; (c) if
; (c) if  such that
such that  in
in  , then
, then  in
in  ; (d) for any
; (d) for any  ,
,  for
for  .
.
Lemma 2.4 (see [24]).
Let  and
and  hold. Assume
hold. Assume  is even, bounded from below,
is even, bounded from below,  and satisfies (PS) condition. Assume that the positive cone
and satisfies (PS) condition. Assume that the positive cone  is an admissible invariant set for
is an admissible invariant set for  and
and  for all
for all  . Suppose there is a linear subspace
. Suppose there is a linear subspace  with
with  , such that
, such that  for some
for some  , where
, where  Then,
Then,  has at least
has at least  pairs of critical points with negative critical values. More precisely,
pairs of critical points with negative critical values. More precisely,
(i)if ,
,  has at least one pair of critical points in
has at least one pair of critical points in and at least
and at least pairs of critical points in
pairs of critical points in
(ii)if
 has at least one pair of critical points in
has at least one pair of critical points in and at least
and at least pairs of critical points in
pairs of critical points in
Lemma 2.5 (see [21]).
Let  and
and  hold. Assume
hold. Assume  is even,
is even,  , and
, and  satisfies (PS) condition. Assume that the positive cone
satisfies (PS) condition. Assume that the positive cone  is an admissible invariant set for
is an admissible invariant set for  and
and  for all
for all  . Suppose there exist linear subspaces
. Suppose there exist linear subspaces  and
and  with
with  ,
,  (
( , resp.),
, resp.),  , such that for some
, such that for some  ,
,  and
and  . Then,
. Then,  has at least
has at least  (
( , resp.) pairs of critical points in
, resp.) pairs of critical points in  with negative critical values.
with negative critical values.
Lemma 2.6 (see [21]).
Let  and
and  hold. Assume
hold. Assume  is even,
is even,  and
and  satisfies (PS) condition. Assume that the positive cone
satisfies (PS) condition. Assume that the positive cone  is an admissible invariant set for
is an admissible invariant set for  and
and  for all
for all  . Suppose there exist linear subspaces
. Suppose there exist linear subspaces  and
and  with
with  ,
,  ,
,  , such that for some
, such that for some  ,
,  and
and  . Then for
. Then for  (
( , resp.),
, resp.),  has at least
has at least  (
( , resp.) pairs of critical points in
, resp.) pairs of critical points in  with positive critical values.
with positive critical values.
Assume  is even,
is even,  , satisfies
, satisfies  and
and  condition for
condition for  . Assume that
. Assume that  is an admissible invariant set for
is an admissible invariant set for  ,
,  for all
for all  .
.  , where
, where  are finite-dimensional subspaces of
are finite-dimensional subspaces of  , and for each
, and for each  , let
, let  and
and  Assume for each
Assume for each  there exist
there exist  such that
such that  , where
, where  ,
,  as
as  . Then,
. Then,  has a sequence of critical points
has a sequence of critical points  such that
such that  as
as  , provided
, provided  for large
for large  .
.
Next, we need some basic concepts of ordered Banach spaces.
Definition 2.8.
An ordered real Banach space is a pair  , where
, where  is a real Banach space and
is a real Banach space and  a closed convex subset of
a closed convex subset of  such that
such that  and
and  . The partial order on
. The partial order on  is given by the cone
is given by the cone  . For
. For  , we write
, we write

If  has nonempty interior, then it is called a solid cone. If every ordered interval is bounded, then
has nonempty interior, then it is called a solid cone. If every ordered interval is bounded, then  is called a normal cone. An operator
is called a normal cone. An operator  is called order preserving (in the literature sometimes increasing) if
is called order preserving (in the literature sometimes increasing) if

strictly order preserving if

and strongly order preserving if

3. Main Results
In this section, we will employ the abstract results in Section 2 to establish some existence theorems on sign-changing solutions of (BVP) (1.2). Firstly, we give some lemmas to change (BVP) (1.2) to a variational problem. Let  be the usual real Banach space with the norm
be the usual real Banach space with the norm  for all
for all  . We can easily verify that
. We can easily verify that

is also a Banach space with respect to  . Let
. Let

then  is a normal solid cone in
is a normal solid cone in  and
and

By  , we denote the usual real Hilbert space with the inner product
, we denote the usual real Hilbert space with the inner product  for all
for all 
It is well known that the solution of (BVP) (1.2) in  is equivalent to the solution of the following integral equation in
is equivalent to the solution of the following integral equation in  :
:

where  is the Green's function of the linear boundary value problem
is the Green's function of the linear boundary value problem  for all
for all  subject to
subject to  that is,
that is,

Define operators  by
by

Since  , (3.4) is equivalent to the following operator equation in
, (3.4) is equivalent to the following operator equation in  :
:

Remark 3.1.
It is easy to see that
-
(i)
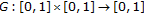 is nonnegative continuous;
is nonnegative continuous; -
(ii)
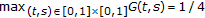 ;
; -
(iii)
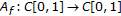 is bounded and continuous.
is bounded and continuous.
Lemma 3.2 (see [20]).
 is a linear completely continuous operator and also a linear completely continuous operator from
is a linear completely continuous operator and also a linear completely continuous operator from  In addition,
In addition,  is strongly order-preserving.
is strongly order-preserving.
From the definition of  , we can obtain that
, we can obtain that  for all
for all  with
with  . Therefore,
. Therefore,  for all
for all  with
with  . It is well known that all eigenvalues of
. It is well known that all eigenvalues of  are
are

which have the corresponding orthonormal eigenfunctions

and  .
.
Lemma 3.3 (see [10]).
 The operator equation
The operator equation

has a solution in  if and only if the operator equation
if and only if the operator equation

has a solution in  .
.
 The uniqueness of the solution for these two above equations is also equivalent.
The uniqueness of the solution for these two above equations is also equivalent.
Remark 3.4.
From the proof of Lemma 3.3 [10], it is very clear if  is a solution for (3.11), then
is a solution for (3.11), then  is a solution for (3.7). Furthermore, if
is a solution for (3.7). Furthermore, if  is a solution for (3.11), then
is a solution for (3.11), then  is a solution for (3.7) with the same sign, which follows from Lemma 3.2.
is a solution for (3.7) with the same sign, which follows from Lemma 3.2.
Lemma 3.5 (see [10]).
Let  ,
,  . Then,
. Then,
(i) is Fréchet differentiable on
is Fréchet differentiable on and
and for all
for all
(ii) is Fréchet differentiable on
is Fréchet differentiable on and
and for all
for all
Choose  and
and  to be our Hilbert space and Banach space, respectively. Define a functional
to be our Hilbert space and Banach space, respectively. Define a functional  :
:

Then, according to Lemma 3.5, we have

Hence, Lemma 3.3 implies that the operator equation  has a solution in
has a solution in  if and only if the functional
if and only if the functional  has a critical point in
has a critical point in  . Thus, (BVP) (1.2) has been transformed into a variational problem.
. Thus, (BVP) (1.2) has been transformed into a variational problem.
We refer the following assumption:
 is continuous and increasing in
is continuous and increasing in  .
.
Lemma 3.6.
Under  ,
,  is satisfied, and
is satisfied, and  is strongly order-preserving.
is strongly order-preserving.
Proof.
The proof is similar to [20], and we omit it here.
Lemma 3.7.
Under  ,
,  is an admissible invariant set for
is an admissible invariant set for  .
.
Proof.
We know that  is strongly order-preserving, so does
is strongly order-preserving, so does  given in Lemma 2.1. The Brezis-Martin theory implies that
given in Lemma 2.1. The Brezis-Martin theory implies that  and
and  are invariant sets under the negative pesudogradient flow of
are invariant sets under the negative pesudogradient flow of  . Requirement (a) is satisfied automatically. For (d), we note that for all
. Requirement (a) is satisfied automatically. For (d), we note that for all  , we have
, we have  , similar to the proof in [23],
, similar to the proof in [23],  . To prove (b), let
. To prove (b), let  for some
for some  , so
, so  , let
, let  be a sequence such that
be a sequence such that  in
in  for some
for some  , then
, then  in
in  . For (c), if
. For (c), if  , then
, then  , if
, if  in
in  , for
, for  , then
, then  and
and  , so
, so  in
in  , and the proof is completed.
, and the proof is completed.
Lemma 3.8 (see [15]).
Any bounded sequence  such that
such that  as
as  has a convergent subsequence.
has a convergent subsequence.
Next, we make more assumptions:
(f
2
) uniformly for
uniformly for  ;
;
(f
3
) , uniformly for
, uniformly for  and some
and some  ;
;
(f
4
) is odd in
is odd in  .
.
Theorem 3.9 (sublinear nonlinearity).
Under  , (BVP) (1.2) has at least one pair of one-sign solutions
, (BVP) (1.2) has at least one pair of one-sign solutions  ,
,  , and at least
, and at least  pairs of nodal solutions
pairs of nodal solutions  for
for  .
.
Proof.
It is easy to see that  and
and  holds.
holds.  is an admissible invariant set for
is an admissible invariant set for  , and
, and  for
for  . Also,
. Also,  is even,
is even,  . By
. By  , there exist
, there exist  ,
,  such that
such that  for all
for all  , then
, then

So  is coercive, bounded from below, and satisfies (PS) condition.
is coercive, bounded from below, and satisfies (PS) condition.
Take  ; from
; from  , there exist
, there exist  ,
,  such that
such that  ,
,  , choose
, choose  , then
, then 
 , and
, and

so  for
for  small. Result follows from Lemma 2.4.
small. Result follows from Lemma 2.4.
Next, we consider an asymptotically linear problem:
(f
5
) uniformly for
uniformly for  ;
;
(f
6
) , uniformly for
, uniformly for  .
.
Theorem 3.10 (asymptotically linear case).
Under  ,
,  ,
,  , and
, and  , (BVP) (1.2) has at least
, (BVP) (1.2) has at least  pairs of nodal solutions provided
pairs of nodal solutions provided  or
or  . Here,
. Here,  , if
, if  ; and
; and  , if
, if  .
.
Proof.
Take  and
and  such that for
such that for  ,
,  . Now let
. Now let  be a (PS) sequence for
be a (PS) sequence for  . Writing
. Writing  with
with  ,
,  , and taking inner product of
, and taking inner product of  and
and  , we see that
, we see that

So  is bounded, where
is bounded, where  . Then,
. Then,  satisfies the (PS) condition.
satisfies the (PS) condition.
If  , let
, let  , and
, and  , then
, then  , and
, and  .
.
From  , we know that there exist
, we know that there exist  and
and  such that
such that

Then, for  ,
,  , we can obtain, when
, we can obtain, when  ,
,

So, choose  , then
, then  .
.
From  , we can get there exist
, we can get there exist  ,
,  such that
such that

Then, when  , we have
, we have

Choose  large enough such that
large enough such that  , and
, and  , result follows from Lemma 2.6.
, result follows from Lemma 2.6.
If  , let
, let  ,
,  , then
, then  ,
,  . From (3.17), when
. From (3.17), when  ,
,

When  , we know from (3.19),
, we know from (3.19),

which means  , then result follows from Lemma 2.5.
, then result follows from Lemma 2.5.
Next, we consider a superlinear problem. Assume that
 there is
there is  such that
such that  for
for  large;
large;
 there are
there are  ,
,  such that
such that  for
for  large.
large.
Theorem 3.11 (superlinear nonlinearity).
Under  ,
,  ,
,  , and
, and  , (BVP) (1.2) has infinitely many nodal solutions.
, (BVP) (1.2) has infinitely many nodal solutions.
Proof.
From condition  by the standard argument,
by the standard argument,  satisfies
satisfies  condition for every
condition for every  . Let
. Let  . From
. From  , we obtain
, we obtain  for all
for all  . Define
. Define  , it is very clear
, it is very clear  and
and  , so
, so  and
and  . So if
. So if  ,
,

Choosing  , we obtain, if
, we obtain, if  and
and  ,
,

Let  . From
. From  , after integrating, we obtain the existence of
, after integrating, we obtain the existence of  such that
such that  for
for  . Hence, we have
. Hence, we have  for
for  and
and  is constant. Therefore, when
is constant. Therefore, when  ,
,

Noting  , choose
, choose  large enough, such that
large enough, such that  , and
, and

Result follows from Lemma 2.7.
Remark 3.12.
If there exist no strict supsolution and supersolution required in [20], just only using the functional  to get the critical point [10, 11], then we just know that (BVP) (1.2) has solutions, even we can know the sign of the critical point of the functional
to get the critical point [10, 11], then we just know that (BVP) (1.2) has solutions, even we can know the sign of the critical point of the functional  because
because  is not strongly order-preserving in
is not strongly order-preserving in  . In our paper, using admissible invariant sets in
. In our paper, using admissible invariant sets in  , we can settle the problem.
, we can settle the problem.
References
Davis JM, Eloe PW, Henderson J: Triple positive solutions and dependence on higher order derivatives. Journal of Mathematical Analysis and Applications 1999,237(2):710-720. 10.1006/jmaa.1999.6500
Davis JM, Henderson J, Wong PJY: General Lidstone problems: multiplicity and symmetry of solutions. Journal of Mathematical Analysis and Applications 2000,251(2):527-548. 10.1006/jmaa.2000.7028
Bai Z, Wang H: On positive solutions of some nonlinear fourth-order beam equations. Journal of Mathematical Analysis and Applications 2002,270(2):357-368. 10.1016/S0022-247X(02)00071-9
Graef JR, Qian C, Yang B: Multiple symmetric positive solutions of a class of boundary value problems for higher order ordinary differential equations. Proceedings of the American Mathematical Society 2003,131(2):577-585. 10.1090/S0002-9939-02-06579-6
Li Y: Positive solutions of fourth-order periodic boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2003,54(6):1069-1078. 10.1016/S0362-546X(03)00127-5
Yao Q: Positive solutions for eigenvalue problems of fourth-order elastic beam equations. Applied Mathematics Letters 2004,17(2):237-243. 10.1016/S0893-9659(04)90037-7
Ruyun M, Jihui Z, Shengmao F: The method of lower and upper solutions for fourth-order two-point boundary value problems. Journal of Mathematical Analysis and Applications 1997,215(2):415-422. 10.1006/jmaa.1997.5639
Bai Z: The method of lower and upper solutions for a bending of an elastic beam equation. Journal of Mathematical Analysis and Applications 2000,248(1):195-202. 10.1006/jmaa.2000.6887
Charkrit S, Kananthai A: Existence of solutions for some higher order boundary value problems. Journal of Mathematical Analysis and Applications 2007,329(2):830-850. 10.1016/j.jmaa.2006.06.092
Li F, Zhang Q, Liang Z: Existence and multiplicity of solutions of a kind of fourth-order boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2005,62(5):803-816. 10.1016/j.na.2005.03.054
Liu X-L, Li W-T: Existence and multiplicity of solutions for fourth-order boundary value problems with parameters. Journal of Mathematical Analysis and Applications 2007,327(1):362-375. 10.1016/j.jmaa.2006.04.021
Li F, Li Y, Liang Z: Existence of solutions to nonlinear Hammerstein integral equations and applications. Journal of Mathematical Analysis and Applications 2006,323(1):209-227. 10.1016/j.jmaa.2005.10.014
Li F, Li Y, Liang Z:Existence and multiplicity of solutions to
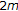 th-order ordinary differential equations. Journal of Mathematical Analysis and Applications 2007,331(2):958-977. 10.1016/j.jmaa.2006.09.025
th-order ordinary differential equations. Journal of Mathematical Analysis and Applications 2007,331(2):958-977. 10.1016/j.jmaa.2006.09.025Han G, Xu Z: Multiple solutions of some nonlinear fourth-order beam equations. Nonlinear Analysis: Theory, Methods & Applications 2008,68(12):3646-3656. 10.1016/j.na.2007.04.007
Yang Y, Zhang J: Existence of solutions for some fourth-order boundary value problems with parameters. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1364-1375. 10.1016/j.na.2007.06.035
Agarwal RP, Kiguradze I: Two-point boundary value problems for higher-order linear differential equations with strong singularities. Boundary Value Problems 2006, 2006:-32.
Perera K, Zhang Z:Multiple positive solutions of singular
 -Laplacian problems by variational methods. Boundary Value Problems 2005,2005(3):377-382. 10.1155/BVP.2005.377
-Laplacian problems by variational methods. Boundary Value Problems 2005,2005(3):377-382. 10.1155/BVP.2005.377Cao D, Noussair ES:Multiplicity of positive and nodal solutions for nonlinear elliptic problems in
 . Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1996,13(5):567-588.
. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1996,13(5):567-588.Cao D, Noussair ES, Yan S: Solutions with multiple peaks for nonlinear elliptic equations. Proceedings of the Royal Society of Edinburgh. Section A 1999,129(2):235-264. 10.1017/S030821050002134X
Han G, Li F: Multiple solutions of some fourth-order boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,66(11):2591-2603. 10.1016/j.na.2006.03.042
Qian A, Li S: Multiple nodal solutions for elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2004,57(4):615-632. 10.1016/j.na.2004.03.010
Chang KC: Infinite-Dimensional Morse Theory and Multiple Solution Problems, Progress in Nonlinear Differential Equations and Their Applications. Birkhäuser, Boston, Mass, USA; 1993:x+312.
Liu Z, Sun J: Invariant sets of descending flow in critical point theory with applications to nonlinear differential equations. Journal of Differential Equations 2001,172(2):257-299. 10.1006/jdeq.2000.3867
Li S, Wang Z-Q: Ljusternik-Schnirelman theory in partially ordered Hilbert spaces. Transactions of the American Mathematical Society 2002,354(8):3207-3227. 10.1090/S0002-9947-02-03031-3
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. American Mathematical Society, Washington, DC, USA; 1986:viii+100.
Acknowledgments
The authors are grateful to the referees for their useful suggestions which have improved the writing of the paper. Jihui Zhang thanks Z. Zhang and the members of AMSS very much for their hospitality and invitation to visit the Academy of Mathematics and Systems Sciences (AMSS), Academia Sinica, in January 2008. The authors also would like to thank Professor D. Cao, Professor S. Li, Professor Y. Ding, and Professor H. Yin for their help and many valuable discussions. This research was supported by the NNSF of China (Grant no.10871096), Foundation of Major Project of Science and Technology of Chinese Education Ministry, SRFDP of Higher Education, and NSF of Education Committee of Jiangsu Province. Zhitao Zhang was supported by NNSF of China (Grant no.10671195).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, Y., Zhang, J. & Zhang, Z. Multiple Nodal Solutions for Some Fourth-Order Boundary Value Problems via Admissible Invariant Sets. Bound Value Probl 2008, 403761 (2008). https://doi.org/10.1155/2008/403761
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/403761
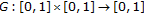 is nonnegative continuous;
is nonnegative continuous;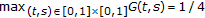 ;
;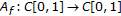 is bounded and continuous.
is bounded and continuous.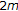 th-order ordinary differential equations. Journal of Mathematical Analysis and Applications 2007,331(2):958-977. 10.1016/j.jmaa.2006.09.025
th-order ordinary differential equations. Journal of Mathematical Analysis and Applications 2007,331(2):958-977. 10.1016/j.jmaa.2006.09.025 -Laplacian problems by variational methods. Boundary Value Problems 2005,2005(3):377-382. 10.1155/BVP.2005.377
-Laplacian problems by variational methods. Boundary Value Problems 2005,2005(3):377-382. 10.1155/BVP.2005.377 . Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1996,13(5):567-588.
. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1996,13(5):567-588.