- Research Article
- Open access
- Published:
Hermitean Cauchy Integral Decomposition of Continuous Functions on Hypersurfaces
Boundary Value Problems volume 2008, Article number: 425256 (2008)
Abstract
We consider Hölder continuous circulant  matrix functions
matrix functions  defined on the Ahlfors-David regular boundary
defined on the Ahlfors-David regular boundary  of a domain
of a domain  in
in  . The main goal is to study under which conditions such a function
. The main goal is to study under which conditions such a function  can be decomposed as
can be decomposed as  , where the components
, where the components  are extendable to two-sided
are extendable to two-sided  -monogenic functions in the interior and the exterior of
-monogenic functions in the interior and the exterior of  , respectively.
, respectively.  -monogenicity is a concept from the framework of Hermitean Clifford analysis, a higher dimensional function theory centered around the simultaneous null solutions of two first-order vector-valued differential operators, called Hermitean Dirac operators.
-monogenicity is a concept from the framework of Hermitean Clifford analysis, a higher dimensional function theory centered around the simultaneous null solutions of two first-order vector-valued differential operators, called Hermitean Dirac operators.  -monogenic functions then are the null solutions of a
-monogenic functions then are the null solutions of a  matrix Dirac operator, having these Hermitean Dirac operators as its entries; such functions have been crucial for the development of function theoretic results in the Hermitean Clifford context.
matrix Dirac operator, having these Hermitean Dirac operators as its entries; such functions have been crucial for the development of function theoretic results in the Hermitean Clifford context.
1. Introduction
Clifford analysis essentially is a higher dimensional function theory offering both a generalization of the theory of holomorphic functions in the complex plane and a refinement of classical multidimensional harmonic analysis. The standard case, nowadays also called Euclidean Clifford analysis, focuses on monogenic functions, that is, the null solutions of the vector-valued Dirac operator  , factorizing the
, factorizing the  -dimensional Laplacian:
-dimensional Laplacian:  . Here
. Here  is an orthonormal basis for the quadratic space
is an orthonormal basis for the quadratic space  underlying the construction of the real Clifford algebra
underlying the construction of the real Clifford algebra  . The fundamental group leaving the Dirac operator invariant is the special orthogonal group
. The fundamental group leaving the Dirac operator invariant is the special orthogonal group  , doubly covered by the spin(
, doubly covered by the spin( ) group of the Clifford algebra
) group of the Clifford algebra  . For this reason, the Dirac operator is called a rotation invariant operator. Standard references for Euclidean Clifford analysis are [1–4].
. For this reason, the Dirac operator is called a rotation invariant operator. Standard references for Euclidean Clifford analysis are [1–4].
In a series of recent papers, the so-called Hermitean Clifford analysis has emerged as yet a refinement of the Euclidean case. One of the ways for introducing it is by considering the complex Clifford algebra  and a so-called complex structure on it, that is, an
and a so-called complex structure on it, that is, an  -element
-element  for which
for which  . It is precisely the requirement that such a complex structure exists, which forces the dimension of the underlying vector space to be even:
. It is precisely the requirement that such a complex structure exists, which forces the dimension of the underlying vector space to be even:  . The resulting function theory focuses on the simultaneous null solutions of two complex Hermitean Dirac operators
. The resulting function theory focuses on the simultaneous null solutions of two complex Hermitean Dirac operators  and
and  which no longer factorize, but still decompose the Laplace operator in the sense that
which no longer factorize, but still decompose the Laplace operator in the sense that  . The fundamental group symmetry of this system breaks down to the action of the special unitary group. The study of complex Dirac operators was initiated in [5–8]; a systematic development of the associated function theory, including the invariance properties with respect to the underlying Lie groups and Lie algebras, is still in full progress (see, e.g., [9–13]).
. The fundamental group symmetry of this system breaks down to the action of the special unitary group. The study of complex Dirac operators was initiated in [5–8]; a systematic development of the associated function theory, including the invariance properties with respect to the underlying Lie groups and Lie algebras, is still in full progress (see, e.g., [9–13]).
In the paper [14], a Cauchy integral formula for Hermitean monogenic functions was established, obviously an essential result in the function theory. However, as in some very particular cases Hermitean monogenicity turns out to be equivalent with anti-holomorphy in  complex variables
complex variables  (see [11]), it was predictable that such a representation formula could not, in the present setting, take the traditional form as in the complex plane or in Euclidean Clifford analysis. Indeed, a matrix approach had to be followed in order to obtain the desired result, leading to the concept of (left or right)
(see [11]), it was predictable that such a representation formula could not, in the present setting, take the traditional form as in the complex plane or in Euclidean Clifford analysis. Indeed, a matrix approach had to be followed in order to obtain the desired result, leading to the concept of (left or right)  -monogenic functions, introduced as circulant
-monogenic functions, introduced as circulant  matrix functions, which are (left or right) null solutions of a
matrix functions, which are (left or right) null solutions of a  circulant matrix Dirac operator, having the Hermitean Dirac operators
circulant matrix Dirac operator, having the Hermitean Dirac operators  and
and  as its entries.
as its entries.
Although the  -monogenic system thus arose as an auxiliary concept in Hermitean Clifford analysis, it deserves to be further studied for its own intrinsic value. In this paper, we consider Hölder continuous circulant
-monogenic system thus arose as an auxiliary concept in Hermitean Clifford analysis, it deserves to be further studied for its own intrinsic value. In this paper, we consider Hölder continuous circulant  matrix functions
matrix functions  defined on the Ahlfors-David regular boundary
defined on the Ahlfors-David regular boundary  of a domain
of a domain  in
in  , and we investigate under which conditions such a function
, and we investigate under which conditions such a function  can be decomposed as
can be decomposed as  , where the components
, where the components  are extendable to two-sided
are extendable to two-sided  -monogenic functions in the interior and the exterior of
-monogenic functions in the interior and the exterior of  , respectively. Such type of decomposition (or "jump") problem was considered already in Euclidean Clifford analysis in, for example, [15].
, respectively. Such type of decomposition (or "jump") problem was considered already in Euclidean Clifford analysis in, for example, [15].
The present decomposition problem is discussed using the matrix Cauchy integral  of
of  (see also [16]) and its singular version
(see also [16]) and its singular version  , called the Hilbert transform; they are shown to be related to each other by Plemelj-Sokhotzki type formulae for the continuous boundary values of
, called the Hilbert transform; they are shown to be related to each other by Plemelj-Sokhotzki type formulae for the continuous boundary values of  . Moreover, a result is obtained connecting the two-sided
. Moreover, a result is obtained connecting the two-sided  -monogenicity of a function
-monogenicity of a function  in
in  to a conservation law for the Hilbert transforms
to a conservation law for the Hilbert transforms  and
and  of its trace on the boundary.
of its trace on the boundary.
2. Preliminaries
Let  be an orthonormal basis of the Euclidean space
be an orthonormal basis of the Euclidean space  , and consider the complex Clifford algebra
, and consider the complex Clifford algebra  constructed over
constructed over  . The noncommutative (also called geometric) multiplication in
. The noncommutative (also called geometric) multiplication in  is governed by the rules
is governed by the rules

The Clifford algebra  thus is generated additively by elements of the form
thus is generated additively by elements of the form  , where
, where  is such that
is such that  , and so the dimension of
, and so the dimension of  is
is  . For
. For  , one puts
, one puts  , the identity element. Any Clifford number
, the identity element. Any Clifford number  may thus be written as
may thus be written as  and its Hermitean conjugate
and its Hermitean conjugate  is defined by
is defined by

where the bar denotes the usual real Clifford algebra conjugation, that is, the main anti-involution for which  , and
, and  denotes the standard complex conjugation. Note that, as any complex Clifford number
denotes the standard complex conjugation. Note that, as any complex Clifford number  may also be written as
may also be written as  ,
,  , the Hermitean conjugation also takes the form
, the Hermitean conjugation also takes the form  .
.
Euclidean space  is embedded in the Clifford algebra
is embedded in the Clifford algebra  by identifying
by identifying  with the real Clifford vector
with the real Clifford vector  given by
given by

The square of  is scalar-valued and equals the norm squared up to a minus sign:
is scalar-valued and equals the norm squared up to a minus sign:  . The Fischer dual of the vector
. The Fischer dual of the vector  is the vector-valued first-order differential operator
is the vector-valued first-order differential operator

called Dirac operator; it is precisely this Dirac operator which underlies the notion of monogenicity of a function, the higher dimensional counterpart of holomorphy in the complex plane. The functions under consideration are defined on an open subset  of
of  and take values in the Clifford algebra
and take values in the Clifford algebra  . They are of the form
. They are of the form  , where the functions
, where the functions  are complex-valued. Whenever a property such as continuity, differentiability, and so forth is ascribed to
are complex-valued. Whenever a property such as continuity, differentiability, and so forth is ascribed to  , it is meant that all the components
, it is meant that all the components  possess the cited property. Such function
possess the cited property. Such function  , assumed to be differentiable in
, assumed to be differentiable in  , is called left monogenic or right monogenic in
, is called left monogenic or right monogenic in  if and only if
if and only if  , or
, or  respectively. Functions which are both left and right monogenic are called two-sided monogenic. As the Dirac operator factorizes the Laplacian
respectively. Functions which are both left and right monogenic are called two-sided monogenic. As the Dirac operator factorizes the Laplacian  , monogenicity can be regarded as a refinement of harmonicity. Within the even part of the Clifford algebra, one can realize the spin group, given by
, monogenicity can be regarded as a refinement of harmonicity. Within the even part of the Clifford algebra, one can realize the spin group, given by

where  denotes the unit sphere containing vectors
denotes the unit sphere containing vectors  for which
for which  . The group
. The group  yields a double cover for the orthogonal group
yields a double cover for the orthogonal group  , defined by the map
, defined by the map  , with
, with  . For a
. For a  -valued function
-valued function  , the induced action of a spin element
, the induced action of a spin element  is given by
is given by  ; it is well known (see [1]) that the Dirac operator commutes with this action, whence we call it rotation invariant.
; it is well known (see [1]) that the Dirac operator commutes with this action, whence we call it rotation invariant.
The transition from the Euclidean Clifford setting described above to Hermitean Clifford analysis now is essentially based on the introduction of a complex structure  . This is a particular element of
. This is a particular element of  , satisfying
, satisfying  . Note that such an element cannot exist when the dimension
. Note that such an element cannot exist when the dimension  of the underlying vector space is odd, whence from now on, we will put
of the underlying vector space is odd, whence from now on, we will put  . In terms of our basis, a particular realization of the complex structure is given by
. In terms of our basis, a particular realization of the complex structure is given by  and
and  . The two projection operators
. The two projection operators  associated to this complex structure
associated to this complex structure  then produce the main objects in the Hermitean Clifford setting by acting upon the corresponding objects in the Euclidean one. First of all, the vector space
then produce the main objects in the Hermitean Clifford setting by acting upon the corresponding objects in the Euclidean one. First of all, the vector space  thus decomposes as
thus decomposes as  into two isotropic subspaces.
into two isotropic subspaces.
The real Clifford vector  is now denoted as
is now denoted as

and the Dirac operator  as
as

while we will also consider their so-called "twisted" counterparts, obtained through the action of  , that is,
, that is,

As was the case with  , a notion of monogenicity may be associated in a natural way to
, a notion of monogenicity may be associated in a natural way to  as well. Note that the vectors
as well. Note that the vectors  and
and  anticommute, as do the Dirac operators
anticommute, as do the Dirac operators  and
and  , while it also holds that
, while it also holds that  and
and  . The projections of the vector variable
. The projections of the vector variable  and the Dirac operator
and the Dirac operator  on the spaces
on the spaces  then give rise to the Hermitean Clifford variables
then give rise to the Hermitean Clifford variables  and
and  , given by
, given by

and (up to a factor) to the Hermitean Dirac operators  and
and  given by
given by

(see [9, 10]). Observe for further use that the Hermitean vector variables and Dirac operators are isotropic, that is,  and
and  , whence the Laplacian allows for the decomposition
, whence the Laplacian allows for the decomposition

while also

These objects lie at the core of the Hermitean function theory by means of the following definition (see, e.g., [9, 10]).
Definition 2.1.
A continuously differentiable function  in
in  with values in
with values in  is called left Hermitean monogenic (or left h-monogenic for short) in
is called left Hermitean monogenic (or left h-monogenic for short) in  , if and only if it satisfies in
, if and only if it satisfies in  the system
the system

or, equivalently, the system

In a similar way, right h-monogenicity is defined. Functions which are both left and right h-monogenic are called two-sided h-monogenic.
This definition inspires the statement that h-monogenicity constitutes a refinement of monogenicity.
The main point of difference between the Hermitean framework and the Euclidean one, is the underlying group invariance of the considered Dirac operators. To this end, we consider the group  , given by
, given by

its definition involving the spin element  corresponding to the complex structure:
corresponding to the complex structure:  . It has been proved that this group constitutes a realization in the Clifford algebra of the unitary group
. It has been proved that this group constitutes a realization in the Clifford algebra of the unitary group  , and moreover, that the Hermitean Dirac operators commute with its associated action. Less precisely, one thus says that these operators are invariant under the action of the unitary group, and so is the notion of h-monogenicity.
, and moreover, that the Hermitean Dirac operators commute with its associated action. Less precisely, one thus says that these operators are invariant under the action of the unitary group, and so is the notion of h-monogenicity.
3. A Pair of Cauchy Integrals and Hilbert Transforms in the Euclidean Setting
From now on, we denote by  a Jordan domain in
a Jordan domain in  , and we put
, and we put  and
and  , where both open sets are assumed to be connected. Furthermore, we assume the boundary
, where both open sets are assumed to be connected. Furthermore, we assume the boundary  of
of  to be a
to be a  -dimensional compact topological and oriented hypersurface, which moreover is Ahlfors-David regular (see [17]). The latter means that there exists a constant
-dimensional compact topological and oriented hypersurface, which moreover is Ahlfors-David regular (see [17]). The latter means that there exists a constant  such that for all
such that for all  and all
and all 

where  denotes the
denotes the  -dimensional Hausdorff measure and
-dimensional Hausdorff measure and  denotes, as usual, the closed ball with radius
denotes, as usual, the closed ball with radius  and centred at the point
and centred at the point  .
.
Now take a function  , that is,
, that is,  is
is  -Hölder continuous on
-Hölder continuous on  , with
, with  . We may then consider the Cauchy integrals
. We may then consider the Cauchy integrals  and
and  in
in  , defined by
, defined by

as well as their respective singular versions  and
and  in
in  , also called Hilbert transforms, defined by
, also called Hilbert transforms, defined by

The so-called Cauchy kernels  and
and  in the above definitions are derived from the fundamental solutions of the Dirac operators
in the above definitions are derived from the fundamental solutions of the Dirac operators  and
and  , and are, respectively, given by
, and are, respectively, given by

where  denotes the surface area of the unit sphere
denotes the surface area of the unit sphere  in
in  . Furthermore,
. Furthermore,

stands for the unit normal vector on  at the point
at the point  (as introduced by Federer, see [18]) and
(as introduced by Federer, see [18]) and  is its twisted counterpart. Note that
is its twisted counterpart. Note that  (resp.,
(resp.,  ) is left monogenic in
) is left monogenic in  with regards to the Dirac operator
with regards to the Dirac operator  (resp.,
(resp.,  ) and that
) and that

For the sake of completeness, we recall some basic properties of the singular Cauchy integrals  and
and  , which are generalizations to the case of Clifford analysis of the properties established in the complex plane as follows:
, which are generalizations to the case of Clifford analysis of the properties established in the complex plane as follows:
(i) and
and  are bounded linear operators on
are bounded linear operators on  ;
;
(ii) and
and  are involutions on
are involutions on  , that is,
, that is,  and
and  for all
for all  ;
;
-
(iii)
the following Plemelj-Sokhotzki formulae hold for any function
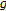 in
in 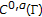 (with
(with 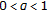 ):
):  (3.7)
(3.7)
Formulae (3.7) express the boundary values of the Cauchy integrals in terms of their singular versions. The study of this boundary behaviour, in the Euclidean Clifford analysis context, has been the subject of intensive research in the last years, see for example [19–23]. We must remark that these formulae also hold for a wider class of rectifiable surfaces, containing as proper subclasses for instance differentiable, chord-arc, piecewise smooth, Liapunov, and Lipschitz surfaces as well as simple Lipschitz graphs.
From the above properties, it is clear that the singular Cauchy integral  gives rise to two important operators, that is,
gives rise to two important operators, that is,

which are mutually complementary projection operators on the same space:  , and
, and  . The same holds for
. The same holds for  , where we introduce
, where we introduce

4. The Hermitean Cauchy Integral: A Matrix Approach
Starting from the pair of fundamental solutions  of the Euclidean Dirac operators
of the Euclidean Dirac operators  and
and  , we now construct the distributions
, we now construct the distributions  and
and  . Explicitly they are given by
. Explicitly they are given by

with

Note that  and
and  are not the fundamental solutions to the respective Hermitean Dirac operators
are not the fundamental solutions to the respective Hermitean Dirac operators  and
and  , but surprisingly, introducing the particular circulant
, but surprisingly, introducing the particular circulant  matrices
matrices

where  is the Dirac delta distribution, one obtains that
is the Dirac delta distribution, one obtains that  , so that
, so that  may be considered as a fundamental solution of the operator
may be considered as a fundamental solution of the operator  in a matricial context. It was exactly this simple observation which has lead to the idea of following a matrix approach in order to establish a Cauchy integral formula and the related function theoretic results in the Hermitean Clifford setting, see [14, 16]. Moreover, it inspired the following definition.
in a matricial context. It was exactly this simple observation which has lead to the idea of following a matrix approach in order to establish a Cauchy integral formula and the related function theoretic results in the Hermitean Clifford setting, see [14, 16]. Moreover, it inspired the following definition.
Definition 4.1.
Let  be continuously differentiable functions defined in
be continuously differentiable functions defined in  and taking values in
and taking values in  , and consider the matrix function
, and consider the matrix function

Then  is called left (resp., right)
is called left (resp., right)  -monogenic in
-monogenic in  if and only if it satisfies in
if and only if it satisfies in  the system
the system

Here  denotes the matrix with zero entries.
denotes the matrix with zero entries.
Explicitly, the system for left  -monogenicity reads
-monogenicity reads

Note that we have found above that  is left (and in fact also right)
is left (and in fact also right)  -monogenic in
-monogenic in  .
.
In general, the  -monogenicity of the matrix function
-monogenicity of the matrix function  does not imply the h-monogenicity of its entry functions
does not imply the h-monogenicity of its entry functions  and
and  . However, choosing in particular
. However, choosing in particular  and
and  , the
, the  -monogenicity of the corresponding diagonal matrix
-monogenicity of the corresponding diagonal matrix  is seen to be equivalent to the h-monogenicity of the function
is seen to be equivalent to the h-monogenicity of the function  .
.
Defining the matrix Laplacian by

we may call the matrix function  harmonic in the domain
harmonic in the domain  if and only if it satisfies the equation
if and only if it satisfies the equation  . It is a simple, yet remarkable, fact that the Dirac matrix
. It is a simple, yet remarkable, fact that the Dirac matrix  still in some sense "factorizes the Laplacian" (as does the Cauchy-Riemann operator in the complex plane) since
still in some sense "factorizes the Laplacian" (as does the Cauchy-Riemann operator in the complex plane) since

This property guarantees that any  -monogenic matrix function
-monogenic matrix function  also is harmonic in
also is harmonic in  , and moreover, its entries are harmonic in the classical sense.
, and moreover, its entries are harmonic in the classical sense.
The above matrix approach will form the key towards the construction of a boundary value theory of h-monogenic functions. In what follows, we will restrict to left monogenicity, unless explicitly stated.
From now on the notations  and
and  are reserved for Clifford vectors associated to points in
are reserved for Clifford vectors associated to points in  . Their Hermitean counterparts are denoted by
. Their Hermitean counterparts are denoted by

while the Hermitean vector pair  still corresponds, as before, to the orthogonal pair
still corresponds, as before, to the orthogonal pair  .
.
Given functions  , we then introduce the vector space
, we then introduce the vector space

and we define, for  , its Hermitean matrix Cauchy integral
, its Hermitean matrix Cauchy integral  to be
to be

which is  -monogenic in
-monogenic in  , that is,
, that is,  in
in  . Here we have introduced the additional circulant matrix
. Here we have introduced the additional circulant matrix

containing (up to a factor) the Hermitean projections  and
and  of the outward unit normal vector
of the outward unit normal vector  at the point
at the point  , given by
, given by

and the matrix Hausdorff measure

A direct calculation reveals that the Hermitean Cauchy integral can be expressed in terms of the Euclidean Cauchy integrals  and
and  as follows:
as follows:

In particular, for the special case of the matrix function  (i.e.,
(i.e.,  and
and  ) this is reduced to
) this is reduced to

Remark 4.2.
It is clear that, in general,  will not turn out to be a diagonal matrix, whence its entries will not be h-monogenic functions. The particular situation where
will not turn out to be a diagonal matrix, whence its entries will not be h-monogenic functions. The particular situation where  , giving rise to an interpretation in terms of h-monogenicity, is explicitly treated below.
, giving rise to an interpretation in terms of h-monogenicity, is explicitly treated below.
We aim at establishing a generalization of the Plemelj-Sokhotzki formulae to the case of  -monogenic matrix functions. To that end, and at the same time inspired by the structure of the above expressions (4.15)-(4.16), let us introduce the singular matrix Cauchy integral
-monogenic matrix functions. To that end, and at the same time inspired by the structure of the above expressions (4.15)-(4.16), let us introduce the singular matrix Cauchy integral

its action on the matrix functions  and
and  being given by matrix multiplication, followed by an operator action on the level of the entries, that is,
being given by matrix multiplication, followed by an operator action on the level of the entries, that is,

Invoking the expressions (4.15)-(4.16) for  in terms of
in terms of  and
and  , and taking into account the Plemelj-Sokhotzki formulae (3.7), the following result is then readily obtained.
, and taking into account the Plemelj-Sokhotzki formulae (3.7), the following result is then readily obtained.
Theorem 4.3.
Let  , then the continuous boundary values of its Hermitean Cauchy integral
, then the continuous boundary values of its Hermitean Cauchy integral  exist and are given by
exist and are given by

Moreover, some properly adapted analogues of the basic properties of  and
and  , mentioned in the previous section, hold for the matrix operator
, mentioned in the previous section, hold for the matrix operator  .
.
Theorem 4.4.
The singular Hermitean Cauchy integral  satisfies the following properties:
satisfies the following properties:
(i) is a bounded linear operator on
is a bounded linear operator on  ;
;
(ii) is an involution on
is an involution on  , that is,
, that is,  , where
, where  is the
is the  identity matrix operator.
identity matrix operator.
Similarly we put

where the operators  and
and  were introduced in (3.8) and the operators
were introduced in (3.8) and the operators  and
and  in (3.9). It is directly seen that
in (3.9). It is directly seen that  , with
, with  and
and  . The following result is then obtained.
. The following result is then obtained.
Theorem 4.5.
The operators  and
and  are mutually complementary projection operators on the same space, that is,
are mutually complementary projection operators on the same space, that is,  and
and  .
.
This theorem entails the direct decomposition

so that each function  admits a unique decomposition into components belonging to
admits a unique decomposition into components belonging to  and
and  , respectively. In what follows, we will use the notations
, respectively. In what follows, we will use the notations

when dealing with left  -monogenic functions. Likewise, in the case of right
-monogenic functions. Likewise, in the case of right  -monogenicity, we will use
-monogenicity, we will use  and
and  .
.
5. The Jump Problem for  -Monogenic Functions
-Monogenic Functions
In this section, we will study the so-called jump (or decomposition) problem for left  -monogenic functions, that is, we will investigate under which conditions a given matrix function
-monogenic functions, that is, we will investigate under which conditions a given matrix function  can be decomposed as
can be decomposed as

where the components  are extendable to left (resp., right)
are extendable to left (resp., right)  -monogenic functions in
-monogenic functions in  , vanishing at infinity. First, it should be noted that if this jump problem has a solution, then it is necessarily unique. This assertion can easily be proved using the Painlevé and Liouville theorems in the Clifford analysis setting, see [1, 15]. Next, under the condition that
, vanishing at infinity. First, it should be noted that if this jump problem has a solution, then it is necessarily unique. This assertion can easily be proved using the Painlevé and Liouville theorems in the Clifford analysis setting, see [1, 15]. Next, under the condition that  , Theorem 4.3 ensures the solvability of the jump problem (5.1) for left
, Theorem 4.3 ensures the solvability of the jump problem (5.1) for left  -monogenic functions, its unique solution is given by
-monogenic functions, its unique solution is given by

The solvability for right  -monogenic functions can be formulated similarly.
-monogenic functions can be formulated similarly.
Now consider the special case of the matrix function  , or equivalently, of a single nonzero entry
, or equivalently, of a single nonzero entry  . The above decomposition problem (5.1) then obviously is strongly connected to the analogous problem for h-monogenic functions, as studied in [24]. In order to be able to rephrase the obtained result (5.2) in the h-monogenic setting, we only need to ensure that
. The above decomposition problem (5.1) then obviously is strongly connected to the analogous problem for h-monogenic functions, as studied in [24]. In order to be able to rephrase the obtained result (5.2) in the h-monogenic setting, we only need to ensure that  is interpretable as an h-monogenic function. In view of this observation and of [24, Remark 1, Theorem 2.2] may be reformulated into the present setting as follows.
is interpretable as an h-monogenic function. In view of this observation and of [24, Remark 1, Theorem 2.2] may be reformulated into the present setting as follows.
Theorem 5.1.
Let  and consider the corresponding matrix function
and consider the corresponding matrix function  . Then the jump problem (5.1) is solvable in terms of h-monogenic functions if and only if
. Then the jump problem (5.1) is solvable in terms of h-monogenic functions if and only if

Proof.
Clearly (5.3) is equivalent to the requirement that  , and thus
, and thus  . The remaining entry
. The remaining entry  of
of  then automatically is an h-monogenic function in
then automatically is an h-monogenic function in  .
.
The next result deals with a necessary and sufficient condition for the extendability of a given matrix function on the hypersurface  to an
to an  -monogenic function in
-monogenic function in  or in
or in  , vanishing at infinity. It is clear that the answer will have to involve the projection operators
, vanishing at infinity. It is clear that the answer will have to involve the projection operators  and
and  .
.
Theorem 5.2.
Let  .
.
-
(i)
In order for
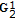 to be the boundary value of a matrix function
to be the boundary value of a matrix function  which is
which is 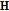 -monogenic in
-monogenic in  , it is necessary and sufficient that
, it is necessary and sufficient that 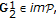 (5.4)
(5.4)
that is, there exists a matrix function  such that
such that  .
.
-
(ii)
In order for
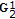 to be the boundary value of a matrix function
to be the boundary value of a matrix function 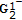 which is
which is 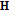 -monogenic in
-monogenic in 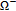 and vanishes at infinity, it is necessary and sufficient that
and vanishes at infinity, it is necessary and sufficient that 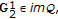 (5.5)
(5.5)
that is, there exists a matrix function  such that
such that  .
.
Proof.
First, let  be the boundary value of an
be the boundary value of an  -monogenic function
-monogenic function  in
in  . Then, as was already shown in [14],
. Then, as was already shown in [14],  is nothing but the Cauchy integral of
is nothing but the Cauchy integral of  , namely,
, namely,

Now let  and let
and let  . Then
. Then  , while, according to Theorem 4.3,
, while, according to Theorem 4.3,  . Thus,
. Thus,  , yielding (5.4). Conversely, assume that (5.4) holds and consider
, yielding (5.4). Conversely, assume that (5.4) holds and consider  given by (5.2), for
given by (5.2), for  . Then
. Then  is an
is an  -monogenic function in
-monogenic function in  and again by Theorem 4.3, we have that
and again by Theorem 4.3, we have that  , which proves (i). Similar considerations apply to (ii).
, which proves (i). Similar considerations apply to (ii).
Remark 5.3.
Condition (5.4) can be rewritten as

and condition (5.5) as

Remark 5.4.
For the special case of the matrix function  , condition (5.7) can be rephrased in terms of the entry function
, condition (5.7) can be rephrased in terms of the entry function  as
as  , which exactly is the criterion for the existence of an
, which exactly is the criterion for the existence of an  -monogenic extension of
-monogenic extension of  to
to  , obtained in [24]. Similarly, in
, obtained in [24]. Similarly, in  , (5.8) yields
, (5.8) yields  .
.
As an application of Theorem 5.2, we consider the Dirichlet boundary value problem for the operator  , which is stated as follows.
, which is stated as follows.
Dirichlet Problem
Given  (
( ), find a function
), find a function  such that
such that

From Theorem 5.2, we immediately see that a solution to this Dirichlet problem will not always exist, as not all functions  are extendable to an -monogenic function in
are extendable to an -monogenic function in  . Indeed, to this end, they need to satisfy condition (5.4) or equivalently, condition (5.7). If this is fulfilled, the solution of the Dirichlet problem will be given, up to a multiplicative constant, by the Cauchy integral of
. Indeed, to this end, they need to satisfy condition (5.4) or equivalently, condition (5.7). If this is fulfilled, the solution of the Dirichlet problem will be given, up to a multiplicative constant, by the Cauchy integral of  , namely,
, namely,

6. A Conservation Law for Two-Sided 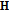 -Monogenic Functions
-Monogenic Functions
This section is devoted to the proof of a remarkable result, establishing a connection between two-sided  -monogenicity of a function
-monogenicity of a function  in a domain
in a domain  and the singular Cauchy integrals
and the singular Cauchy integrals  and
and  of its trace on the boundary
of its trace on the boundary  of
of  . We still mention that, in the context of Euclidean Clifford analysis, a similar "conservation law" was obtained in [25] for two-sided monogenicity.
. We still mention that, in the context of Euclidean Clifford analysis, a similar "conservation law" was obtained in [25] for two-sided monogenicity.
Theorem 6.1.
Let  , such that
, such that  in
in  . Then the following statements are equivalent:
. Then the following statements are equivalent:
(i) is two-sided
is two-sided  -monogenic in
-monogenic in  ;
;
(ii) .
.
Proof.
Suppose that, next to its already assumed left  -monogenicity,
-monogenicity,  also is right
also is right  -monogenic in
-monogenic in  . Then it holds that
. Then it holds that  , whence
, whence

Conversely, suppose that  . From the assumed left
. From the assumed left  -monogenicity of
-monogenicity of  , we have that
, we have that  and that for
and that for  the boundary value taken from the inside, denoted by
the boundary value taken from the inside, denoted by  , is given by
, is given by

In view of the assumption made, we thus have

Now put  . Then
. Then  is right
is right  -monogenic in
-monogenic in  and belongs to
and belongs to  , with
, with

Next, put  . Then
. Then  is harmonic in
is harmonic in  and it belongs to
and it belongs to  with
with  on
on  . The Dirichlet problem for harmonic matrix functions then implies that
. The Dirichlet problem for harmonic matrix functions then implies that  in
in  or
or  in
in  . Consequently,
. Consequently,  is also right
is also right  -monogenic in
-monogenic in  .
.
In the next theorem, we will show how the requirement  in the formulation of Theorem 6.1 can be avoided.
in the formulation of Theorem 6.1 can be avoided.
Theorem 6.2.
Let  be a continuous matrix function with trace
be a continuous matrix function with trace  . Then
. Then  is two-sided
is two-sided  -monogenic in
-monogenic in  if and only if it is harmonic in
if and only if it is harmonic in  and
and

Proof.
Suppose that  is two-sided
is two-sided  -monogenic in
-monogenic in  . By Cauchy's integral formula (see [14]), we have that
. By Cauchy's integral formula (see [14]), we have that

The Plemelj-Sokhotzki formulae (see Theorem 4.3) then imply that

Consequently,  for all
for all  . Conversely, assume that
. Conversely, assume that  is harmonic in
is harmonic in  and
and  . Let us define the matrix functions
. Let us define the matrix functions

They are left and right  -monogenic, respectively, and hence both are harmonic in
-monogenic, respectively, and hence both are harmonic in  . Combining Theorems 4.3 and 4.4, we can assert that
. Combining Theorems 4.3 and 4.4, we can assert that  and
and  are also continuous on
are also continuous on  . As
. As  is harmonic in
is harmonic in  and
and  , it follows that
, it follows that  for
for  . The proof is completed by showing that
. The proof is completed by showing that  in
in  .
.
7. Main Theorem
Theorem 7.1.
Let  . Then the following statements are equivalent:
. Then the following statements are equivalent:
(i) can be decomposed as in (5.1), the components
can be decomposed as in (5.1), the components  being extendable to two-sided
being extendable to two-sided  -monogenic functions in
-monogenic functions in  , vanishing at infinity;
, vanishing at infinity;
(ii) is a two-sided
is a two-sided  -monogenic in
-monogenic in  .
.
Proof.
Assuming (i) to hold, we may directly check, invoking Theorem 5.2, that  . We thus get that
. We thus get that  , which yields (ii) in view of Theorem 6.1. This completes the proof since the inverse implication is trivial.
, which yields (ii) in view of Theorem 6.1. This completes the proof since the inverse implication is trivial.
References
Brackx F, Delanghe R, Sommen F: Clifford Analysis, Research Notes in Mathematics. Volume 76. Pitman, Boston, Mass, USA; 1982:x+308.
Delanghe R, Sommen F, Soucek V: Clifford Algebra and Spinor-Valued Functions, Mathematics and Its Applications. Volume 53. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xviii+485.
Gürlebeck K, Sprößig W: Quaternionic and Clifford Calculus for Physicists and Engineers. John Wiley & Sons, Chichester, UK; 1998.
Gilbert JE, Murray MAM: Clifford Algebras and Dirac Operators in Harmonic Analysis, Cambridge Studies in Advanced Mathematics. Volume 26. Cambridge University Press, Cambridge, UK; 1991:viii+334.
Ryan J: Complexified Clifford analysis. Complex Variables: Theory & Application 1982,1(1):119-149.
Rocha-Chávez R, Shapiro M, Sommen F: Integral Theorems for Functions and Differential Forms in Cm, Chapman & Hall/CRC Research Notes in Mathematics. Volume 428. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:x+204.
Sabadini I, Sommen F: Hermitian Clifford analysis and resolutions. Mathematical Methods in the Applied Sciences 2002,25(16–18):1395-1413.
Colombo F, Sabadini I, Sommen F, Struppa DC: Analysis of Dirac Systems and Computational Algebra, Progress in Mathematical Physics. Volume 39. Birkhäuser, Boston, Mass, USA; 2004:xiv+332.
Brackx F, De Schepper H, Sommen F: The Hermitian Clifford analysis toolbox. accepted for Advances in Applied Clifford Algebras
Brackx F, Bureš J, De Schepper H, Eelbode D, Sommen F, Soucek V: Fundaments of Hermitean Clifford analysis. I. Complex structure. Complex Analysis and Operator Theory 2007,1(3):341-365. 10.1007/s11785-007-0010-5
Brackx F, Bureš J, De Schepper H, Eelbode D, Sommen F, Soucek V:Fundaments of Hermitean Clifford analysis. II. Splitting of
 -monogenic equations. Complex Variables and Elliptic Equations 2007,52(10-11):1063-1079. 10.1080/17476930701466614
-monogenic equations. Complex Variables and Elliptic Equations 2007,52(10-11):1063-1079. 10.1080/17476930701466614Eelbode D: Zonal Hermitean monogenic functions. Proceedings of the 15th International Conference on Finite or Infinite Dimensional Complex Analysis and Applications (ICFIDCAA '07), July-August 2007, Osaka, Japan
Sommen F, Peña-Peña D: A Martinelli-Bochner formula for the Hermitian Dirac equation. Mathematical Methods in the Applied Sciences 2007,30(9):1049-1055. 10.1002/mma.824
Brackx F, De Knock B, De Schepper H, Peña-Peña D, Sommen F: On Cauchy and Martinelli-Bochner integral formulae in Hermitean Clifford analysis. submitted
Abreu-Blaya R, Bory-Reyes J, Peña-Peña D: Jump problem and removable singularities for monogenic functions. The Journal of Geometric Analysis 2007,17(1):1-13. 10.1007/s00039-006-0585-4
Brackx F, De Knock B, De Schepper H: A matrix Hilbert transform in Hermitean Clifford analysis. Journal of Mathematical Analysis and Applications 2008,344(2):1068-1078. 10.1016/j.jmaa.2008.03.043
David G, Semmes S: Analysis of and on Uniformly Rectifiable Sets, Mathematical Surveys and Monographs. Volume 38. American Mathematical Society, Providence, RI, USA; 1993:xii+356.
Federer H: Geometric Measure Theory, Die Grundlehren der Mathematischen Wissenschaften, Band 153. Springer, New York, NY, USA; 1969:xiv+676.
Abreu Blaya R, Peña-Peña D, Bory Reyes J:Clifford Cauchy type integrals on Ahlfors-David regular surfaces in
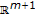 . Advances in Applied Clifford Algebras 2003,13(2):133-156. 10.1007/s00006-003-0008-7
. Advances in Applied Clifford Algebras 2003,13(2):133-156. 10.1007/s00006-003-0008-7Abreu-Blaya R, Bory-Reyes J, Gerus OF, Shapiro M: The Clifford-Cauchy transform with a continuous density: N. Davydov's theorem. Mathematical Methods in the Applied Sciences 2005,28(7):811-825. 10.1002/mma.594
Abreu Blaya R, Bory Reyes J, Moreno García T: Minkowski dimension and Cauchy transform in Clifford analysis. Complex Analysis and Operator Theory 2007,1(3):301-315. 10.1007/s11785-007-0015-0
Abreu-Blaya R, Bory-Reyes J, Moreno García T: Cauchy transform on nonrectifiable surfaces in Clifford analysis. Journal of Mathematical Analysis and Applications 2008,339(1):31-44. 10.1016/j.jmaa.2007.06.040
Bory Reyes J, Abreu Blaya R: Cauchy transform and rectifiability in Clifford analysis. Zeitschrift für Analysis und ihre Anwendungen 2005,24(1):167-178.
Abreu Blaya R, Bory Reyes J, Peña-Peña D, Sommen F: A boundary value problem for Hermitian monogenic functions. Boundary Value Problems 2008, 2008:-7.
Abreu Blaya R, Bory Reyes J, Delanghe R, Sommen F: Cauchy integral decomposition of multi-vector valued functions on hypersurfaces. Computational Methods and Function Theory 2005,5(1):111-134.
Acknowledgments
This paper was written while R. Abreu Blaya and J. Bory Reyes were visiting the Department of Mathematical Analysis of Ghent University. They were supported by the Special Research Fund no. 01T00807, obtained for the collaboration between the Clifford Research Group Ghent and the Cuban Research Group in Clifford analysis, on a project entitled Boundary Values Theory in Clifford Analysis. The authors wish to thank all members of this Department for their kind hospitality.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Blaya, R., Reyes, J., Brackx, F. et al. Hermitean Cauchy Integral Decomposition of Continuous Functions on Hypersurfaces. Bound Value Probl 2008, 425256 (2008). https://doi.org/10.1155/2008/425256
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/425256
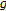 in
in 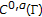 (with
(with 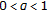 ):
): 
 -Monogenic Functions
-Monogenic Functions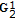 to be the boundary value of a matrix function
to be the boundary value of a matrix function  which is
which is 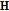 -monogenic in
-monogenic in  , it is necessary and sufficient that
, it is necessary and sufficient that 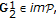
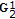 to be the boundary value of a matrix function
to be the boundary value of a matrix function 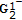 which is
which is 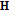 -monogenic in
-monogenic in 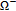 and vanishes at infinity, it is necessary and sufficient that
and vanishes at infinity, it is necessary and sufficient that 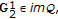
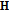 -Monogenic Functions
-Monogenic Functions -monogenic equations. Complex Variables and Elliptic Equations 2007,52(10-11):1063-1079. 10.1080/17476930701466614
-monogenic equations. Complex Variables and Elliptic Equations 2007,52(10-11):1063-1079. 10.1080/17476930701466614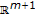 . Advances in Applied Clifford Algebras 2003,13(2):133-156. 10.1007/s00006-003-0008-7
. Advances in Applied Clifford Algebras 2003,13(2):133-156. 10.1007/s00006-003-0008-7