- Research Article
- Open access
- Published:
Blowup for a Non-Newtonian Polytropic Filtration System Coupled via Nonlinear Boundary Flux
Boundary Value Problems volume 2008, Article number: 847145 (2008)
Abstract
We study the global existence and the global nonexistence of a non-Newtonian polytropic filtration system coupled via nonlinear boundary flux. We first establish a weak comparison principle, then discuss the large time behavior of solutions by using modified upper and lower solution methods and constructing various upper and lower solutions. Necessary and sufficient conditions on the global existence of all positive (weak) solutions are obtained.
1. Introduction
In this paper, we consider the following Neumann problem:



where  ,
,  ,
,  is a bounded domain with smooth boundary
is a bounded domain with smooth boundary  ,
,  is the outward normal vector on the boundary
is the outward normal vector on the boundary  ,
,  , and
, and  are positive and satisfy the compatibility conditions.
are positive and satisfy the compatibility conditions.
Parabolic equations like (1.1) appear in population dynamics, chemical reactions, heat transfer, and so on. In particular, (1.1) may be used to describe the nonstationary flows in a porous medium of fluids with a power dependence of the tangential stress on the velocity of displacement under polytropic conditions. In this case, (1.1) are called the non-Newtonian polytropic filtration equations (see [ 1, 2, 3, 4, 5, 6] and the references therein). For the Neuman problem (1.1)–(1.3), the local existence of solutions in time has been established, see survey in [4].
Recall the single quasilinear parabolic equation with nonlinear boundary condition

with  . It is known that the solutions of (1.4) exist globally if and only if
. It is known that the solutions of (1.4) exist globally if and only if  for
for  ; they exist globally if and only if
; they exist globally if and only if  when
when  (see [7–10]).
(see [7–10]).
In [11, 12], M. Wang and S. Wang studied the following nonlinear diffusion system with nonlinear boundary conditions

with  . In [11], they obtained the necessary and sufficient conditions to the global existence of solutions for
. In [11], they obtained the necessary and sufficient conditions to the global existence of solutions for  . In [12], they considered the case of
. In [12], they considered the case of  or
or  and obtained the necessary and sufficient blowup conditions for the special case
and obtained the necessary and sufficient blowup conditions for the special case  (the ball centered at the origin in
(the ball centered at the origin in  with radius
with radius  ). However, for the general domain
). However, for the general domain  , they only gave some sufficient conditions to the global existence and the blowup of solutions.
, they only gave some sufficient conditions to the global existence and the blowup of solutions.
In [2], Wang considered the following system with nonlinear boundary conditions:

with  . They obtained the necessary and sufficient conditions on the global existence of all positive (weak) solutions.
. They obtained the necessary and sufficient conditions on the global existence of all positive (weak) solutions.
Sun and Wang in [13] studied the nonlinear equation with nonlinear boundary condition

They proved that all positive (weak) solutions of (1.7) exist globally if and only if  when
when  ; they exist globally if and only if
; they exist globally if and only if  when
when  .
.
The main purpose of this paper is to study the influence of nonlinear power exponents on the existence and nonexistence of global solutions of (1.1)–(1.3). By using upper- and lower-solution methods, we obtain the necessary and sufficient conditions on the existence of global (weak) solutions to (1.1)–(1.3). Our main results are stated as follows.
Theorem 1.1.
If  , then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if
, then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if  and
and  .
.
Theorem 1.2.
If  , then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if
, then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if  and
and  .
.
Theorem 1.3.
If  , then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if
, then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if  and
and  .
.
Theorem 1.4.
If  , then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if
, then all positive (weak) solutions of (1.1)–(1.3) exist globally if and only if  and
and  .
.
Remark 1.5.
If  , the results in [11] are included in Theorem 1.4, and if
, the results in [11] are included in Theorem 1.4, and if  or
or  , Theorems 1.1–1.3 improve the results of [12].
, Theorems 1.1–1.3 improve the results of [12].
Remark 1.6.
If we extend the solution to (1.6) to the interval  by symmetry, we get a solution to the same problem (1.6) with the condition at
by symmetry, we get a solution to the same problem (1.6) with the condition at  , substituted by a condition at
, substituted by a condition at  ,
, 
 Conversely, symmetric solutions to this latter problem are solutions to the original problem (1.6). The problem (1.1)–(1.3) is the more general
Conversely, symmetric solutions to this latter problem are solutions to the original problem (1.6). The problem (1.1)–(1.3) is the more general  -dimensional version of the problem (1.6). Theorems 1.1–1.4 extend the results of the problem (1.6) into multidimensional case and it seems to be a natural extension of Wang [2].
-dimensional version of the problem (1.6). Theorems 1.1–1.4 extend the results of the problem (1.6) into multidimensional case and it seems to be a natural extension of Wang [2].
Remark 1.7.
If  , the conclusions of Theorems 1.1 and 1.4 are consistent with those of the single equation (1.7). This paper generalizes the results of the single equation (1.7) to the system (1.1)–(1.3).
, the conclusions of Theorems 1.1 and 1.4 are consistent with those of the single equation (1.7). This paper generalizes the results of the single equation (1.7) to the system (1.1)–(1.3).
The rest of this paper is organized as follows. Some preliminaries will be given in Section 2 . Theorems 1.1–1.4 will be proved in Sections 3–5, respectively.
2. Preliminaries
As it is well known that degenerate and singular equations need not possess classical solutions, we give a precise definition of a weak solution to (1.1)–(1.3).
Definition 2.1.
Let  and
and  . A vector function
. A vector function  is called a weak upper (or lower) solution to (1.1)–(1.3) in
is called a weak upper (or lower) solution to (1.1)–(1.3) in  if
if
(i) ;
;
(ii) ;
;
(iii)for any positive two functions  one has
one has

In particular,  is called a weak solution of (1.1)–(1.3) if it is both a weak upper and a lower solution. For every
is called a weak solution of (1.1)–(1.3) if it is both a weak upper and a lower solution. For every  , if
, if  is a solution of (1.1)–(1.3) in
is a solution of (1.1)–(1.3) in  , we say that
, we say that  is global.
is global.
Next we give some preliminary propositions and lemmas.
Proposition 2.2 (comparison principle).
Assume that  are positive
are positive  functions and
functions and  is any weak solution of (1.1)–(1.3). Also assume that
is any weak solution of (1.1)–(1.3). Also assume that  and
and  are a lower and an upper solution of (1.1)–(1.3) in
are a lower and an upper solution of (1.1)–(1.3) in  , respectively, with nonlinear boundary flux
, respectively, with nonlinear boundary flux  and
and  , where
, where  . Then we have
. Then we have  in
in  .
.
Proof.
For small  , letting
, letting  and setting
and setting  , according to the definition of upper and lower solutions, we have
, according to the definition of upper and lower solutions, we have

Define

As in [14], by letting  we get
we get

that is,

where  . Similarly, we have
. Similarly, we have

Since  and
and  , it follows from the continuity of
, it follows from the continuity of  and
and  that there exists a
that there exists a  sufficiently small such that
sufficiently small such that  for
for  . It follows from (2.5) and (2.6) that
. It follows from (2.5) and (2.6) that  in
in  .
.
Denote  . We claim that
. We claim that  . Otherwise, from the continuity of
. Otherwise, from the continuity of  and
and  there exists
there exists  such that
such that  and
and  for all
for all  By (2.5) and (2.6) we obtain that
By (2.5) and (2.6) we obtain that  in
in  , which contradicts the definition of
, which contradicts the definition of  . Hence
. Hence  for all
for all 
Obviously,  is a lower solution of (1.1)–(1.3) in
is a lower solution of (1.1)–(1.3) in  . Therefore,
. Therefore,  in
in  . Using this fact, as in the above proof we can prove that
. Using this fact, as in the above proof we can prove that  in
in  .
.
For convenience, we denote  , which are fixed constants, and let
, which are fixed constants, and let  .
.
Proposition 2.3.
Assume  and that
and that  or
or  holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
Proof.
Without loss of generality, assume  . Consider the single equation
. Consider the single equation

We know from [13] that  blows up in finite time. Since
blows up in finite time. Since  , by the comparison principle,
, by the comparison principle,  is a lower solution of (1.1)–(1.3) and
is a lower solution of (1.1)–(1.3) and  blows up in finite time if
blows up in finite time if  .
.
The following propositions can be proved in the similar procedure.
Proposition 2.4.
Assume  and that
and that  or
or  holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
Proposition 2.5.
Assume  and that
and that  or
or  holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
Proposition 2.6.
Assume  and that
and that  or
or  holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
holds. Then the solutions of (1.1)–(1.3) blow up in finite time.
Let  be the first eigenfunction of
be the first eigenfunction of

with the first eigenvalue  , normalized by
, normalized by  , then
, then  in
in  and
and  and
and  on
on  (see [15–17]).
(see [15–17]).
Thus there exist some positive constants  such that
such that

We have also  provided
provided  with
with  and some positive constant
and some positive constant  . For the fixed
. For the fixed  , there exists a positive constant
, there exists a positive constant  such that
such that  if
if 
At the end of this section, we describe two simple lemmas without proofs.
Lemma 2.7.
Suppose that positive constants  satisfy
satisfy  , then for any two positive constants
, then for any two positive constants  , there exist two positive constants
, there exist two positive constants  such that
such that  and
and  .
.
Lemma 2.8.
For any constant  , there exist positive constants
, there exist positive constants  which depend only on
which depend only on  and
and  such that
such that

where  is a positive bounded function.
is a positive bounded function.
3. Proof of Theorem 1.1
Lemma 3.1.
Suppose  ,
,  . Then all positive solutions of (1.1)–(1.3) exist globally.
. Then all positive solutions of (1.1)–(1.3) exist globally.
Proof .
Construct

where  if
if  ,
,  if
if  , and
, and  if
if  ,
,  if
if  ,
,  are defined in (2.8) and (2.9),
are defined in (2.8) and (2.9),  are positive constants to be determined,
are positive constants to be determined,  and
and

We know that  since
since  for any
for any  . Thus for
. Thus for  a simple computation shows
a simple computation shows

In addition, we have

Similarly, we can get

Noting  on
on  , we have on the boundary that
, we have on the boundary that

Since  , there exist constants
, there exist constants  large such that
large such that

By (3.3)–(3.7), we know that  is a global upper solution of (1.1)–(1.3). The global existence of solutions to (1.1)–(1.3) follows from the comparison principle.
is a global upper solution of (1.1)–(1.3). The global existence of solutions to (1.1)–(1.3) follows from the comparison principle.
Lemma 3.2.
Suppose  ,
,  . Then all positive solutions of (1.1)–(1.3) blow up in finite time.
. Then all positive solutions of (1.1)–(1.3) blow up in finite time.
Proof .
Case 1.
 . Let
. Let  if
if  ,
,  if
if  , and
, and  if
if  ,
,  if
if  . In light of
. In light of  , we choose
, we choose  such that
such that

For the above  , we set
, we set  where
where  ,
,  , and
, and


By a direct computation, for  , we obtain that
, we obtain that


If  , we have
, we have  and thus
and thus

On the other hand, since  for any
for any  , we have
, we have

We have by (3.10), (3.13), and (3.14) that  for
for  .
.
If  , then
, then  and hence
and hence

We follow from (3.10), (3.11), and (3.15) that  for
for  .
.
Similarly, we can get  for
for  also.
also.
We have on the boundary that


Moreover, by (3.8) we have that

Equations (3.9), (3.16)–(3.18) imply that  Therefore
Therefore  is a lower solution of (1.1)–(1.3).
is a lower solution of (1.1)–(1.3).
Case 2.
 . Set
. Set  as above with
as above with 
Case 3.
 . Set
. Set  as above with
as above with 
Case 4.
 . Set
. Set 
By similar arguments, we conform that  is a lower solution of (1.1)–(1.3), which blows up in finite time. We know by the comparison principle that the solution
is a lower solution of (1.1)–(1.3), which blows up in finite time. We know by the comparison principle that the solution  blows up in finite time.
blows up in finite time.
We get the proof of Theorem 1.1 by combining Proposition 2.3 and Lemmas 3.1 and 3.2.
4. Proof of Theorems 1.2 and 1.3
Lemma 4.1.
Suppose  with
with  . Then all positive solutions of (1.1)–(1.3) exist globally.
. Then all positive solutions of (1.1)–(1.3) exist globally.
Proof .
Take

for  , where
, where  if
if  ,
,  if
if  ,
,  satisfying
satisfying  , and constants
, and constants  are to be determined. By performing direct calculations, we have, for
are to be determined. By performing direct calculations, we have, for  ,
,

By setting  if
if  ,
,  if
if  , we have on the boundary that
, we have on the boundary that

Since  , by Lemma 2.7 there exist two positive constants
, by Lemma 2.7 there exist two positive constants  such that
such that  ,
,  , and
, and

Set  By arguments in Lemma 3.1, for
By arguments in Lemma 3.1, for  , we have
, we have

On the other hand, since  , there exist two positive constants
, there exist two positive constants  such that
such that


By (4.2)–(4.7), it follows that  is an upper solution of (1.1)–(1.3). Thus the solutions of (1.1)–(1.3) are global.
is an upper solution of (1.1)–(1.3). Thus the solutions of (1.1)–(1.3) are global.
Lemma 4.2.
Suppose  with
with  . Then all positive solutions of (1.1)–(1.3) blow up in finite time.
. Then all positive solutions of (1.1)–(1.3) blow up in finite time.
Proof .
We first prove that there exist  such that
such that

When  ,
,  yields
yields  Hence there exist
Hence there exist  such that
such that  Set
Set  , and
, and 
When  , take
, take  ,
, 
When  , take
, take  ,
, 
Let  if
if  ,
,  if
if  , and
, and  ,
,  ,
,  .
.
Define  where
where  , and
, and


By a direct computation, for  , we have
, we have

By similar arguments in Lemma 3.2, we have  for
for  .
.
Moreover, for  , we have
, we have

By (4.8), we have

By (4.9), (4.12), and (4.13), we have that  is a lower solution of (1.1) and (1.3), which with the comparison principle implies that the solutions of (1.1)–(1.3) blow up in finite time.
is a lower solution of (1.1) and (1.3), which with the comparison principle implies that the solutions of (1.1)–(1.3) blow up in finite time.
It has been shown from Proposition 2.4 and Lemmas 4.1 and 4.2 that Theorem 1.2 is true.
In a similar way to the proof of Theorem 1.2, we have Theorem 1.3.
5. Proof of Theorem 1.4
Lemma 5.1.
Suppose  with
with  . Then all positive solutions of (1.1)–(1.3) exist globally.
. Then all positive solutions of (1.1)–(1.3) exist globally.
Proof .
Take  where
where  and
and  are the undetermined positive constants.
are the undetermined positive constants.
Calculating directly for  , we have by Lemma 2.8 that
, we have by Lemma 2.8 that

Let  if
if  ,
,  if
if  , and
, and  if
if  ,
,  if
if  . We have on the boundary that
. We have on the boundary that

Since  we know by Lemma 2.8 that there exist constants
we know by Lemma 2.8 that there exist constants  such that
such that

For the above constants  , we choose a constant
, we choose a constant  so large that
so large that

By (5.1)–(5.4), we know that  is an upper solution of (1.1)–(1.3), Thus the solutions of (1.1)–(1.3) are global.
is an upper solution of (1.1)–(1.3), Thus the solutions of (1.1)–(1.3) are global.
Lemma 5.2.
Suppose  with
with  . Then all positive solutions of (1.1)–(1.3) blow up in finite time.
. Then all positive solutions of (1.1)–(1.3) blow up in finite time.
Proof .
We first prove that there exist  such that
such that

In fact, when  ,
,  yields
yields  . Hence there exists
. Hence there exists  such that
such that  . Set
. Set  and
and 
When  and
and  , take
, take 

When  and
and  , let
, let 

Take  , and
, and  , where
, where  , and
, and


By a direct computation for  , we have
, we have


For  , we have
, we have

Moreover, (5.5) implies

It follows from (5.6), (5.8)–(5.11) that  is a lower solution of (1.1)–(1.3). Because
is a lower solution of (1.1)–(1.3). Because  blows up in finite time, and so does
blows up in finite time, and so does  .
.
By Proposition 2.6 and Lemmas 5.1 and 5.2, we see that Theorem 1.4 holds.
References
Tan Z, Liu XG: Non-Newton filtration equation with nonconstant medium void and critical Sobolev exponent. Acta Mathematica Sinica 2004,20(2):367-378. 10.1007/s10114-004-0361-z
Wang S: Doubly nonlinear degenerate parabolic systems with coupled nonlinear boundary conditions. Journal of Differential Equations 2002,182(2):431-469. 10.1006/jdeq.2001.4101
Wang Z, Yin J, Wang C: Critical exponents of the non-Newtonian polytropic filtration equation with nonlinear boundary condition. Applied Mathematics Letters 2007,20(2):142-147. 10.1016/j.aml.2006.03.008
Wu Z, Zhao J, Yin J, Li H: Nonlinear Diffusion Equations. World Scientific, River Edge, NJ, USA; 2001:xviii+502.
Yang Z, Lu Q: Nonexistence of positive solutions to a quasilinear elliptic system and blow-up estimates for a non-Newtonian filtration system. Applied Mathematics Letters 2003,16(4):581-587. 10.1016/S0893-9659(03)00040-5
Yang Z, Lu Q: Blow-up estimates for a quasi-linear reaction-diffusion system. Mathematical Methods in the Applied Sciences 2003,26(12):1005-1023. 10.1002/mma.409
Song X, Zheng S: Blow-up analysis for a quasilinear parabolic system with multi-coupled nonlinearities. Journal of Mathematical Analysis and Applications 2003,281(2):739-756. 10.1016/S0022-247X(03)00256-7
Wang M, Wu Y: Global existence and blow-up problems for quasilinear parabolic equations with nonlinear boundary conditions. SIAM Journal on Mathematical Analysis 1993,24(6):1515-1521. 10.1137/0524085
Wang M: The long-time behavior of solutions to a class of quasilinear parabolic equations with nonlinear boundary conditions. Acta Mathematica Sinica 1996,39(1):118-124.
Wolanski N: Global behavior of positive solutions to nonlinear diffusion problems with nonlinear absorption through the boundary. SIAM Journal on Mathematical Analysis 1993,24(2):317-326. 10.1137/0524021
Wang M, Wang S: Quasilinear reaction-diffusion systems with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 1999,231(1):21-33. 10.1006/jmaa.1998.6220
Wang M: Fast-slow diffusion systems with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2001,46(6):893-908. 10.1016/S0362-546X(00)00156-5
Sun WJ, Wang S: Nonlinear degenerate parabolic equation with nonlinear boundary condition. Acta Mathematica Sinica 2005,21(4):847-854. 10.1007/s10114-004-0512-2
Alt HW, Luckhaus S: Quasilinear elliptic-parabolic differential equations. Mathematische Zeitschrift 1983,183(3):311-341. 10.1007/BF01176474
Lindqvist P:On the equation
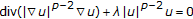 . Proceedings of the American Mathematical Society 1990,109(1):157-164.
. Proceedings of the American Mathematical Society 1990,109(1):157-164.Lindqvist P:Addendum to on the equation
 . Proceedings of the American Mathematical Society 1992,116(2):583-584.
. Proceedings of the American Mathematical Society 1992,116(2):583-584.Li Y, Xie C:Blow-up for
 -Laplacian parabolic equations. Electronic Journal of Differential Equations 2003,2003(20):1-12.
-Laplacian parabolic equations. Electronic Journal of Differential Equations 2003,2003(20):1-12.
Acknowledgments
This work was partially supported by NNSF of China (10771226), was partially supported by Natural Science Foundation Project of CQ CSTC (2007BB0124), and was partially supported by Natural Science Foundation Project of China West Normal University (07B047).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Z., Mu, C. & Li, Y. Blowup for a Non-Newtonian Polytropic Filtration System Coupled via Nonlinear Boundary Flux. Bound Value Probl 2008, 847145 (2008). https://doi.org/10.1155/2008/847145
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/847145
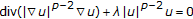 . Proceedings of the American Mathematical Society 1990,109(1):157-164.
. Proceedings of the American Mathematical Society 1990,109(1):157-164. . Proceedings of the American Mathematical Society 1992,116(2):583-584.
. Proceedings of the American Mathematical Society 1992,116(2):583-584. -Laplacian parabolic equations. Electronic Journal of Differential Equations 2003,2003(20):1-12.
-Laplacian parabolic equations. Electronic Journal of Differential Equations 2003,2003(20):1-12.