- Research Article
- Open access
- Published:
Existence and Iteration of Positive Solutions for One-Dimensional  -Laplacian Boundary Value Problems with Dependence on the First-Order Derivative
-Laplacian Boundary Value Problems with Dependence on the First-Order Derivative
Boundary Value Problems volume 2008, Article number: 860414 (2008)
Abstract
This paper deals with the existence and iteration of positive solutions for the following one-dimensional  -Laplacian boundary value problems:
-Laplacian boundary value problems:  ,
,  , subject to some boundary conditions. By making use of monotone iterative technique, not only we obtain the existence of positive solutions for the problems, but also we establish iterative schemes for approximating the solutions.
, subject to some boundary conditions. By making use of monotone iterative technique, not only we obtain the existence of positive solutions for the problems, but also we establish iterative schemes for approximating the solutions.
1. Introduction
In this paper, we are concerned with the existence and iteration of positive solutions for the following one-dimensional  -Laplacian boundary value problems:
-Laplacian boundary value problems:

subject to one of the following boundary conditions:

or

where  with
with  and
and  satisfy the following:
satisfy the following:
(H1) is continuous;
is continuous;
( )
) is continuous;
is continuous;
(H2) is nondecreasing in
is nondecreasing in  for all
for all  , that is,
, that is,  for all
for all  ;
;
( )
) is nondecreasing in
is nondecreasing in  for all
for all  , that is,
, that is,  for all
for all  ;
;
(H3) is measurable, and
is measurable, and  is not identically zero on any compact subinterval of
is not identically zero on any compact subinterval of  . Furthermore,
. Furthermore,  satisfies
satisfies  .
.
Here, a positive solution of (1.1), (1.2) or (1.1), (1.3) means a solution  of (1.1), (1.2) or (1.1), (1.3) satisfying
of (1.1), (1.2) or (1.1), (1.3) satisfying  .
.
The boundary value problems (1.1), (1.2) and (1.1), (1.3) deserve a special mention because these forms occur in the study of the  -dimensional
-dimensional  -Laplacian equation, non-Newtonian fluid theory and turbulent flow of a gas in a porous medium [1].
-Laplacian equation, non-Newtonian fluid theory and turbulent flow of a gas in a porous medium [1].
A consistent account on the existing literature on equation

is provided and it emphasizes the use of upper and lower solution technique and the fixed point theory, for instance, Krasnoselskii fixed point theorem, the fixed point index of a completely continuous operator with respect to a cone in a Banach space, one may see [2–5] and the references therein. In [6], by using the monotone iterative technique, Ma et al. obtained the existence of monotone positive solution and established the corresponding iterative schemes of (1.4) under the multipoint boundary value condition. However, in their discussion, the nonlinear term  is not involved with the first-order derivative
is not involved with the first-order derivative  .
.
Recently, there is much attention focused on the study of the boundary value problems like (1.1) which the nonlinear term  is involved with the first-order derivative explicitly. In [7], Bai et al. considered the boundary value problems (1.1), (1.2) and (1.1), (1.3) and they proved that problems (1.1), (1.2) and (1.1), (1.3) possessed at least three positive solutions by applying a fixed point theorem due to Avery and Peterson [8]. In [9], the authors also deal with the boundary value problem (1.1), (1.2) via Krasnoselskii fixed point theorem. Here, we should mention that Sun and Ge [10] have got the positive solution of the boundary value problem (1.1), (1.2) by making use of monotone iterative technique.
is involved with the first-order derivative explicitly. In [7], Bai et al. considered the boundary value problems (1.1), (1.2) and (1.1), (1.3) and they proved that problems (1.1), (1.2) and (1.1), (1.3) possessed at least three positive solutions by applying a fixed point theorem due to Avery and Peterson [8]. In [9], the authors also deal with the boundary value problem (1.1), (1.2) via Krasnoselskii fixed point theorem. Here, we should mention that Sun and Ge [10] have got the positive solution of the boundary value problem (1.1), (1.2) by making use of monotone iterative technique.
On the other hand, when  is involved with the first-order derivative explicitly, we can see easily that the results obtained in [1, 7, 9] are only the existence of positive solutions under some suitable conditions. Seeing such a fact, it is an interesting problem which shows how to find these solutions since they exist definitely. Motivated by the above-mentioned results, by making use of the classical monotone iterative technique, we will investigate not only the existence of positive solutions for the boundary value problems (1.1), (1.2) and (1.1), (1.3), but also give iterative schemes for approximating the solutions. Unlike the idea of [10], we will construct a special subset
is involved with the first-order derivative explicitly, we can see easily that the results obtained in [1, 7, 9] are only the existence of positive solutions under some suitable conditions. Seeing such a fact, it is an interesting problem which shows how to find these solutions since they exist definitely. Motivated by the above-mentioned results, by making use of the classical monotone iterative technique, we will investigate not only the existence of positive solutions for the boundary value problems (1.1), (1.2) and (1.1), (1.3), but also give iterative schemes for approximating the solutions. Unlike the idea of [10], we will construct a special subset  (see Section 3) and look at
(see Section 3) and look at  or
or  as a unit to overcome difficulties when
as a unit to overcome difficulties when  depends on both
depends on both  and
and  . It is worth starting that the first term of our iterative schemes are simple functions which are determined with some linear ordinary equations and cone
. It is worth starting that the first term of our iterative schemes are simple functions which are determined with some linear ordinary equations and cone  (see Remark 3.2). Therefore, the iterative schemes are significant and feasible. At the same time, we will correct some mistakes in [11–13] (see Remark 3.5).
(see Remark 3.2). Therefore, the iterative schemes are significant and feasible. At the same time, we will correct some mistakes in [11–13] (see Remark 3.5).
This paper is organized as follows. After this section, some definitions and lemmas will be established in Section 2. In Section 3, we will give our main results Theorems 3.1 and 3.4. Finally, an example is also presented to illustrate our results in Section 4.
2. Preliminaries
In this section, we provide some background material from the theory of cones in Banach spaces. We also state some lemmas which are important to proof our main results.
Definition 2.1.
Let  be a real Banach space. A nonempty closed set
be a real Banach space. A nonempty closed set  is called a cone, if it satisfies the following two conditions:
is called a cone, if it satisfies the following two conditions:
(i) for all
for all  and all
and all  ;
;
(ii) implies
implies  .
.
Definition 2.2.
A map  is said to be concave on
is said to be concave on  , if
, if

for all  and
and 
Consider the Banach space  equipped with the norm
equipped with the norm

and define the cone  by
by

Lemma 2.3 (see {[3]}).
If  , then
, then  , where
, where  .
.
Define the operator  as follows:
as follows:

Lemma 2.4.
Assume ( ), (
), ( ) hold, then
) hold, then  is completely continuous.
is completely continuous.
Proof.
From ( ), (
), ( ), it is obviously that
), it is obviously that  . Since
. Since  , we can see that
, we can see that  is continuous and nonincreasing on
is continuous and nonincreasing on  , that is,
, that is,  is concave on
is concave on  , so
, so  is well defined. The continuity of
is well defined. The continuity of  is clear because of the continuity of
is clear because of the continuity of  and
and  . Now, we will prove that
. Now, we will prove that  is compact. Let
is compact. Let  be a bounded set, then there exists
be a bounded set, then there exists  , such that
, such that  . For any
. For any  , we have
, we have 
 , then we have
, then we have

The Arzela-Ascoli theorem guarantees that  is relatively compact, which means that
is relatively compact, which means that  is compact. Then
is compact. Then  is completely continuous.
is completely continuous.
Lemma 2.5.
Assume ( ), (
), ( ) and (
) and ( ) hold. If
) hold. If  such that
such that  , then
, then  .
.
Proof.
Noticing that  is nondecreasing in
is nondecreasing in  , the proof is simple, here we omit it.
, the proof is simple, here we omit it.
3. Main Results
For convenience, we denote

where  . It is easy to see that
. It is easy to see that  .
.
Theorem 3.1.
Assume ( ), (
), ( ), and (
), and ( ) hold. Moreover, suppose that there exist six constants
) hold. Moreover, suppose that there exist six constants  , with
, with  and
and  , such that
, such that
(H4) ;
;
(H5) .
.
Then the boundary value problem (1.1), (1.2) has at least two nonincreasing positive solutions  and
and  with
with

and  , where
, where

 and
and  are arbitrary constants which satisfy
are arbitrary constants which satisfy  .
.
Proof.
We denote a set  by
by

Based on the preceding preliminaries, we can divide our proof into three steps.
Step 1.
We first prove  . Let
. Let  , note that
, note that  is nonincreasing on
is nonincreasing on  , then
, then

By Lemma 2.3, we have

Since  is nondecreasing in
is nondecreasing in  , and by assumptions (H4) and (H5), we obtain
, and by assumptions (H4) and (H5), we obtain

which imply that

On the other hand, for  , we have
, we have

In virtue of (3.8)-(3.9),  .
.
Step 2.
Let  ,
,  is an arbitrary constant which satisfies
is an arbitrary constant which satisfies  , then
, then  . Hence,
. Hence,  . Let
. Let  , next we claim that
, next we claim that  . Indeed, it is easy to check that
. Indeed, it is easy to check that

Using assumptions  and
and  , we have
, we have 
 , these imply that
, these imply that

Therefore,  . We denote
. We denote

Since  From Lemma 2.4,
From Lemma 2.4,  is compact, we assert that
is compact, we assert that  has a convergent subsequence
has a convergent subsequence  and there exists
and there exists  , such that
, such that  . Now, since
. Now, since  , for
, for  , we have
, we have

This combined with Lemma 2.5 gives

so

By induction,

Hence, we assert that  . Let
. Let  in (3.12) to obtain
in (3.12) to obtain  since
since  is continuous. Since
is continuous. Since  and
and  is a nonnegative concave function on
is a nonnegative concave function on  , we conclude that
, we conclude that  . It is well known that the fixed point of operator
. It is well known that the fixed point of operator  is the solution of the boundary value problem (1.1), (1.2). Therefore,
is the solution of the boundary value problem (1.1), (1.2). Therefore,  is a positive, nonincreasing solution of the boundary value problem (1.1), (1.2).
is a positive, nonincreasing solution of the boundary value problem (1.1), (1.2).
Step 3.
Put  ,
,  is an arbitrary constant satisfying
is an arbitrary constant satisfying  , then
, then  . Hence,
. Hence,  . From the definition of
. From the definition of  and
and  , we derive that
, we derive that

Setting  , in what follows, we will prove that
, in what follows, we will prove that  . In fact, similar to (3.10)-(3.11), combined with the above inequalities, one has
. In fact, similar to (3.10)-(3.11), combined with the above inequalities, one has

We deduce from (3.18) that  . Denote
. Denote

Since  , from Lemma 2.4, we have
, from Lemma 2.4, we have

By Lemma 2.5, we get

so  . By induction,
. By induction,  Hence, we assert that
Hence, we assert that  , and
, and  . Therefore,
. Therefore,  is a positive, nonincreasing solution of the boundary value problem (1.1), (1.2).
is a positive, nonincreasing solution of the boundary value problem (1.1), (1.2).
Remark 3.2.
-
(i)
We can easily get that
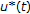 and
and 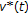 are the maximal and minimal solutions of the boundary value problem (1.1), (1.2) in
are the maximal and minimal solutions of the boundary value problem (1.1), (1.2) in  . Of course
. Of course 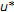 and
and 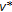 may coincide and then the boundary value problem (1.1), (1.2) has only one solution in
may coincide and then the boundary value problem (1.1), (1.2) has only one solution in 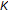 .
. -
(ii)
It is worth pointing out that
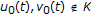 . In fact,
. In fact, 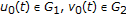 , which are determined with some linear ordinary equations and the cone
, which are determined with some linear ordinary equations and the cone  , this is different from the results in [6, 10], where
, this is different from the results in [6, 10], where 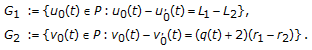 (3.22)
(3.22)
Corollary 3.3.
Assume (H1), (H2) and (H3) hold, suppose that
(H6) ;
;
(H7) .
.
(Particularly,  ). Then there exist four constants
). Then there exist four constants  , with
, with 
 , such that the boundary value problem (1.1), (1.2) has at least two nonincreasing positive solutions
, such that the boundary value problem (1.1), (1.2) has at least two nonincreasing positive solutions  and
and  with
with

and  , where
, where

 and
and  are arbitrary constants which satisfy
are arbitrary constants which satisfy  .
.
Proof.
It is very easy to verify the conditions (H4) and (H5) can be obtained from (H6) and (H7), so we omit the proof.
Obviously, though the similar arguments of Theorem 3.1, we could get the following theorem.
Theorem 3.4.
Assume ( ), (
), ( ) and (
) and ( ) hold, suppose that there exist six positive constants
) hold, suppose that there exist six positive constants  , with
, with  and
and  , such that
, such that
(H8) ;
;
(H9) .
.
Then the boundary value problem (1.1), (1.3) has at least two nondecreasing positive solutions  and
and  with
with

and  , where
, where

 and
and  are arbitrary constants which satisfy
are arbitrary constants which satisfy  .
.
Remark 3.5.
In [11], Liu and Zhang studied the following boundary value problem:

where  and
and  is an increasing positive homomorphism and homeomorphism with
is an increasing positive homomorphism and homeomorphism with  (for more details, see [11–13]). In that paper, the authors claimed that
(for more details, see [11–13]). In that paper, the authors claimed that  is a solution if and only if
is a solution if and only if  is a solution of the following integral equation:
is a solution of the following integral equation:

where  , if
, if  ;
;  , if
, if  , otherwise
, otherwise  is a solution of the equation
is a solution of the equation

where

Unfortunately, such a claim is incorrect since

Similar reason, the results in [12, 13] are also incorrect, as they deal with the nonlinear systems. Under the boundary condition (1.3), we could avoid (3.31) to occur. With the similar argument of Theorem 3.4, we could have the similar theorem to Theorem 3.4 for the following boundary value problem:

Here, we omit the proofs.
4. Example
In this section, we will give an example to illustrate our results.
Example 4.1.
Consider the boundary value problem

where  with
with  , take
, take  ,
,

we have  and
and  . Take
. Take  , we get
, we get  . Choose
. Choose  , and
, and  , so
, so  satisfies the following:
satisfies the following:
(1) is continuous;
is continuous;
(2) is nondecreasing in
is nondecreasing in  for all
for all  ;
;
(3)
 ;
;
(4)
 .
.
Therefore, by Theorem 3.1, the boundary value problem (4.1) has at least two nonincreasing positive solutions  and
and  , such that
, such that

and  , where
, where

 and
and  are arbitrary constants which satisfy
are arbitrary constants which satisfy  .
.
For  the two iterative schemes are
the two iterative schemes are  ,
,  is arbitrary constant with
is arbitrary constant with 

 ,
,  is arbitrary constant with
is arbitrary constant with 

Remark 4.2.
The nonlinear term  in
in  is nonincreasing, so the results in [10] do not hold.
is nonincreasing, so the results in [10] do not hold.
References
O'Regan D:Some general existence principles and results for
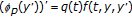 ,
,  SIAM Journal on Mathematical Analysis 1993,24(3):648-668. 10.1137/0524040
SIAM Journal on Mathematical Analysis 1993,24(3):648-668. 10.1137/0524040Jiang D, Gao W:Upper and lower solution method and a singular boundary value problem for the one-dimensional
 -Laplacian. Journal of Mathematical Analysis and Applications 2000,252(2):631-648. 10.1006/jmaa.2000.7012
-Laplacian. Journal of Mathematical Analysis and Applications 2000,252(2):631-648. 10.1006/jmaa.2000.7012Wang J:The existence of positive solutions for the one-dimensional
 -Laplacian. Proceedings of the American Mathematical Society 1997,125(8):2275-2283. 10.1090/S0002-9939-97-04148-8
-Laplacian. Proceedings of the American Mathematical Society 1997,125(8):2275-2283. 10.1090/S0002-9939-97-04148-8Guo Y, Ge W:Three positive solutions for the one-dimensional
 -Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1
-Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1Kong L, Wang J:Multiple positive solutions for the one-dimensional
 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2000,42(8):1327-1333. 10.1016/S0362-546X(99)00143-1
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2000,42(8):1327-1333. 10.1016/S0362-546X(99)00143-1Ma D-X, Du Z-J, Ge W-G:Existence and iteration of monotone positive solutions for multipoint boundary value problem with
 -Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016
-Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016Bai Z, Gui Z, Ge W:Multiple positive solutions for some
 -Laplacian boundary value problems. Journal of Mathematical Analysis and Applications 2004,300(2):477-490. 10.1016/j.jmaa.2004.06.053
-Laplacian boundary value problems. Journal of Mathematical Analysis and Applications 2004,300(2):477-490. 10.1016/j.jmaa.2004.06.053Avery RI, Peterson AC: Three positive fixed points of nonlinear operators on ordered Banach spaces. Computers & Mathematics with Applications 2001,42(3–5):313-322.
Wang Z, Zhang J:Positive solutions for one-dimensional
 -Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012
-Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012Sun B, Ge W:Existence and iteration of positive solutions for some
 -Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(6):1820-1830. 10.1016/j.na.2006.08.025
-Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(6):1820-1830. 10.1016/j.na.2006.08.025Liu B, Zhang J: The existence of positive solutions for some nonlinear boundary value problems with linear mixed boundary conditions. Journal of Mathematical Analysis and Applications 2005,309(2):505-516. 10.1016/j.jmaa.2004.09.036
Liu B, Zhang J: The existence of positive solutions for some nonlinear equation systems. Journal of Mathematical Analysis and Applications 2006,324(2):970-981. 10.1016/j.jmaa.2005.12.049
Ji D, Feng H, Ge W: The existence of symmetric positive solutions for some nonlinear equation systems. Applied Mathematics and Computation 2008,197(1):51-59. 10.1016/j.amc.2007.07.031
Acknowledgments
The project is supported by Foundation of Major Project of Science and Technology of Chinese Education Ministry, SRFDP of Higher Education, NSF of Education Committee of Jiangsu Province, and Graduate Innovation Foundation of Jiangsu Province (1612005022).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Z., Zhang, J. Existence and Iteration of Positive Solutions for One-Dimensional  -Laplacian Boundary Value Problems with Dependence on the First-Order Derivative.
Bound Value Probl 2008, 860414 (2008). https://doi.org/10.1155/2008/860414
-Laplacian Boundary Value Problems with Dependence on the First-Order Derivative.
Bound Value Probl 2008, 860414 (2008). https://doi.org/10.1155/2008/860414
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/860414
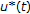 and
and 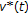 are the maximal and minimal solutions of the boundary value problem (1.1), (1.2) in
are the maximal and minimal solutions of the boundary value problem (1.1), (1.2) in  . Of course
. Of course 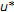 and
and 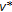 may coincide and then the boundary value problem (1.1), (1.2) has only one solution in
may coincide and then the boundary value problem (1.1), (1.2) has only one solution in 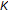 .
.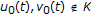 . In fact,
. In fact, 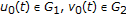 , which are determined with some linear ordinary equations and the cone
, which are determined with some linear ordinary equations and the cone  , this is different from the results in [
, this is different from the results in [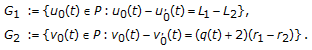
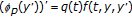 ,
,  SIAM Journal on Mathematical Analysis 1993,24(3):648-668. 10.1137/0524040
SIAM Journal on Mathematical Analysis 1993,24(3):648-668. 10.1137/0524040 -Laplacian. Journal of Mathematical Analysis and Applications 2000,252(2):631-648. 10.1006/jmaa.2000.7012
-Laplacian. Journal of Mathematical Analysis and Applications 2000,252(2):631-648. 10.1006/jmaa.2000.7012 -Laplacian. Proceedings of the American Mathematical Society 1997,125(8):2275-2283. 10.1090/S0002-9939-97-04148-8
-Laplacian. Proceedings of the American Mathematical Society 1997,125(8):2275-2283. 10.1090/S0002-9939-97-04148-8 -Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1
-Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2000,42(8):1327-1333. 10.1016/S0362-546X(99)00143-1
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2000,42(8):1327-1333. 10.1016/S0362-546X(99)00143-1 -Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016
-Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016 -Laplacian boundary value problems. Journal of Mathematical Analysis and Applications 2004,300(2):477-490. 10.1016/j.jmaa.2004.06.053
-Laplacian boundary value problems. Journal of Mathematical Analysis and Applications 2004,300(2):477-490. 10.1016/j.jmaa.2004.06.053 -Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012
-Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012 -Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(6):1820-1830. 10.1016/j.na.2006.08.025
-Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(6):1820-1830. 10.1016/j.na.2006.08.025