- Research Article
- Open access
- Published:
On the Solvability of Second-Order Impulsive Differential Equations with Antiperiodic Boundary Value Conditions
Boundary Value Problems volume 2008, Article number: 864297 (2008)
Abstract
We prove existence results for second-order impulsive differential equations with antiperiodic boundary value conditions in the presence of classical fixed point theorems. We also obtain the expression of Green's function of related linear operator in the space of piecewise continuous functions.
1. Introduction and Preliminaries
Many evolution processes are characterized by the fact that at certain moments of time they experience a change of state abruptly. Consequently, it is natural to assume that these perturbations act instantaneously, that is, in the form of impulses. It is known that many biological phenomena involving threshold, bursting rhythm models in medicine and biology, optimal control models in economics, pharmacokinetics, and frequency modulated systems do exhibit impulse effects. The branch of modern, applied analysis known as "impulsive" differential equations provides a natural framework to mathematically describe the aforementioned jumping processes. The reader is referred to monographs [1–4] and references therein for some nice examples and applications to the above areas.
In this paper, we mainly study the following second-order impulsive differential equations with antiperiodic boundary value conditions:

where  and
and  is continuous on
is continuous on  ,
,  are continuous functions.
are continuous functions.
In [4–12], the authors studied the existence of antiperiodic solutions for first-order, second-order, or high-order differential equations without impulses, and in [3, 13–16] the authors were concerned with the antiperiodic solutions of first-order impulsive differential equations. Also we should mention the work by Cabada et al. in [17] which is concerned with a certain  th order linear differential equation with constant impulses at fixed times and nonhomogeneous periodic boundary conditions. So far, to the best of our knowledge, this is the first work to deal with the antiperiodic solutions to second-order differential equations with nonconstant impulses. Our method to prove the existence of antiperiodic solutions is based on the works in [13, 18, 19]. We should point out that it is Christopher C. Tisdell who started with this method.
th order linear differential equation with constant impulses at fixed times and nonhomogeneous periodic boundary conditions. So far, to the best of our knowledge, this is the first work to deal with the antiperiodic solutions to second-order differential equations with nonconstant impulses. Our method to prove the existence of antiperiodic solutions is based on the works in [13, 18, 19]. We should point out that it is Christopher C. Tisdell who started with this method.
The article is organized as follows. In Section 2, we present the expression of Green's functions of related linear operator in the space of piecewise continuous functions. Section 3 contains the main results of the paper and is devoted to the existence of solutions to (1.1). There, differential inequalities are developed and applied to prove the existence of at least one solution to (1.1). In Section 4, a couple of examples are given to illustrate how the main results work.
To understand the notation used above and the ideas in the remainder of the paper, we now briefly introduce some appropriate concepts connected with impulsive differential equations. Most of the following notation can be found in [1, 2, 4, 5]. We assume that  ,
,  exist and
exist and  . We introduce and denote the Banach space
. We introduce and denote the Banach space  by
by

with the norm  where
where  is the usual Euclidean norm and
is the usual Euclidean norm and  will be the Euclidean inner product.
will be the Euclidean inner product.
In a similar fashion to the above, define and denote the Banach space  by
by

with the norm 
The following fixed point theorem is our main tool to prove the existence of at least one solution to (1.1).
Schaefer's Fixed Point Theorem (19)
Let  be a Banach space and let
be a Banach space and let  be a completely continuous operator. Then, either
be a completely continuous operator. Then, either
-
(i)
the operator equation
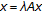 has a solution for
has a solution for 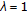 , or
, or -
(ii)
the set
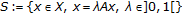 is unbounded.
is unbounded.
2. Expression of Green's Function
In this part, we present the expression of Green's functions for second order impulsive equations with antiperiodic conditions.
Lemma 2.1.
Assume  and
and  are two constants. Let
are two constants. Let  ,
,  . Then for any
. Then for any  ,
,  solves
solves

if and only if  is the solution of integral equation
is the solution of integral equation

where


Proof.
Assume  is a solution of (2.1) and let
is a solution of (2.1) and let  for
for  . We have
. We have

Then for  ,
,

This implies  . Consequently, from the impulsive condition in (2.1) we get that
. Consequently, from the impulsive condition in (2.1) we get that

where  . Now we integrate (2.3) from
. Now we integrate (2.3) from  to
to  and use (2.5) to obtain
and use (2.5) to obtain

It follows that

Similarly, we have for  that
that

To sum up, we have for  that
that

Since  , we can deduce in a similar way as to deal with
, we can deduce in a similar way as to deal with  to obtain
to obtain

Now we are in position to show the expression of  for
for  To do that, we need to compute
To do that, we need to compute  in (2.10). In what follows we present the expression of
in (2.10). In what follows we present the expression of  for
for  step by step and then obtain the general form of
step by step and then obtain the general form of  for
for  .
.
First of all, for  , we have
, we have

See that

Consequently,

Integrate  by parts to get
by parts to get

Thus,

Similarly, we have for  that
that

Now we consider  for
for  . Clearly,
. Clearly,

Noting that  , we have
, we have

where  is denoted by
is denoted by  Similarly, for
Similarly, for  there holds
there holds

Thus, for  ,
,

By the boundary condition of (2.1), we have

Substituting (2.21) into (2.20), and also noting that for 

we see that  is the solution of (2.2).
is the solution of (2.2).
Now assume  is a solution of (2.2). Then for
is a solution of (2.2). Then for 


It is easy to verify

For  we compute straightforwardly to get
we compute straightforwardly to get

which implies

Now, we prove  is a solution of (2.1). Then the proof is completed.
is a solution of (2.1). Then the proof is completed.
For later use, we present the following estimations:

Corollary 2.2.
Assume in (2.1) that  and
and  . Then for any
. Then for any  ,
,  is the solution of
is the solution of

if and only if  is the solution of integral equation
is the solution of integral equation

where

Obviously, there hold

We now give Green's function of (2.1) for  .
.
Lemma 2.3.
For any  ,
,  is the solution of
is the solution of

if and only if  satisfies the integral equation
satisfies the integral equation

where

Since the proof is very similar to that of Lemma 2.1, we omit it here. We can check easily that  satisfies (2.34) and hence
satisfies (2.34) and hence  is a solution of (2.33). Also we get by straightforward computation that
is a solution of (2.33). Also we get by straightforward computation that

Recall that a mapping between Banach spaces is compact if it is continuous and carries bounded sets into relatively compact sets.
Lemma 2.4.
Suppose that  and
and  are continuous. Define an operator
are continuous. Define an operator  as
as

where  and
and  are as given in Lemma 2.1. Then
are as given in Lemma 2.1. Then  is a compact map.
is a compact map.
Proof.
Noting the continuity of  and
and  , this follows in a standard step-by-step process and so it is omitted.
, this follows in a standard step-by-step process and so it is omitted.
3. Main Results
In this section, we prove the existence results for (1.1) in presence of Schaefer's fixed-point theorem.
Theorem 3.1.
Suppose that  and
and  are continuous. If for some
are continuous. If for some  and
and  , there exist nonnegative constants
, there exist nonnegative constants  , and
, and  such that
such that



where  is the Euclidean inner product,
is the Euclidean inner product,  . Then (1.1) has at least one solution.
. Then (1.1) has at least one solution.
Proof.
Define an integral operator  as
as

where  and
and  follow the forms of (G) and (H) in Lemma 2.1. By Lemma 2.4,
follow the forms of (G) and (H) in Lemma 2.1. By Lemma 2.4,  is a compact mapping. Also, it follows from Lemma 2.1 that
is a compact mapping. Also, it follows from Lemma 2.1 that  is a fixed point of
is a fixed point of  if and only if
if and only if  satisfies
satisfies

which is equivalent to (1.1). Consequently, all that we need to do is to verify that  has at least one fixed point. With this in mind, we assume
has at least one fixed point. With this in mind, we assume  is a solution of
is a solution of

That is,

It is equivalent to say that  satisfies
satisfies

Firstly, we see that for  ,
,

Further more, by the antiperiodic boundary condition we have

As a result,

Now we show that any potential solution of (3.6) is bounded a priori. By (3.2) and (3.11), we obtain

Taking the supremum and rearranging, we get by (3.3) that

Differentiating both sides of (3.7) and noting (2.23), we obtain

where

Thus,

Now we have shown that any possible solution of (3.6) is bounded by  which is independent of
which is independent of  . By Scheafer's fixed theorem we know that
. By Scheafer's fixed theorem we know that  has at least one fixed point. Therefore, the proof is completed.
has at least one fixed point. Therefore, the proof is completed.
Suppose both  and
and  in Theorem 3.1. We obtain the following theorem.
in Theorem 3.1. We obtain the following theorem.
Theorem 3.2.
Assume that  and
and  are continuous. If for some
are continuous. If for some  there exist nonnegative constants
there exist nonnegative constants  , and
, and  such that
such that

where  is the Euclidean inner product,
is the Euclidean inner product,  , then (1.1) has at least one solution.
, then (1.1) has at least one solution.
Proof.
Consider the mapping


where

By Lemma 2.4,  is a compact mapping. Consider the equation
is a compact mapping. Consider the equation

To show that  has at least one fixed point, we apply Schaefer's theorem by showing that all potential solutions to
has at least one fixed point, we apply Schaefer's theorem by showing that all potential solutions to

are bounded a priori, with the bound being independent of  . With this in mind, let
. With this in mind, let  be a solution of (3.23). Note that
be a solution of (3.23). Note that  is also a solution to
is also a solution to

On one hand, we see that for 

On the other hand, by the antiperiodic boundary condition we have

It therefore follows that

Consequently,

where  .
.
We compute directly to get

Differentiating both sides of (3.19), we obtain

where

Thus,

Then the proof is completed.
Similarly, we can prove the following existence result for  in Theorem 3.2.
in Theorem 3.2.
Theorem 3.3.
Suppose that  and
and  are continuous. If there exist nonnegative constants
are continuous. If there exist nonnegative constants  and
and  such that
such that

where  is the Euclidean inner product,
is the Euclidean inner product,  , then (1.1) has at least one solution.
, then (1.1) has at least one solution.
4. Examples
In this part, we show how our main theorems work by a couple of examples.
Example 4.1.
The scalar second-order impulsive equations with antiperiodic boundary value condition

where  have at least one solution.
have at least one solution.
Proof.
Let  and
and  in Theorem 3.1. For
in Theorem 3.1. For  , we have
, we have  and
and

On the other hand, for 

Noting  , we have for
, we have for  and
and  that
that

Moreover,  ,
,  . Then the conclusion follows from Theorem 3.1.
. Then the conclusion follows from Theorem 3.1.
Example 4.2.
Consider antiperiodic value problem

We claim that (4.5) has at least one solution.
Proof.
Let  and
and  in Theorem 3.2. Choosing
in Theorem 3.2. Choosing  , we have for
, we have for  that
that

Since  , we have
, we have  Thus, for
Thus, for  and
and  ,
,

Moreover,  ,
,  . Then the conclusion follows from Theorem 3.2.
. Then the conclusion follows from Theorem 3.2.
References
Bainov D, Simeonov PS: Impulsive Differential Equations: Periodic Solutions and Applications, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 66. Longman Scientific & Technical, Harlow, UK; 1993:x+228.
Benchohra M, Henderson J, Ntouyas S: Impulsive Differential Equations and Inclusions, Contemporary Mathematics and Its Applications. Volume 2. Hindawi, New York, NY, USA; 2006:xiv+366.
Franco D, Nieto JJ: First-order impulsive ordinary differential equations with anti-periodic and nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2000,42(2):163-173. 10.1016/S0362-546X(98)00337-X
Park JY, Ha TG: Existence of antiperiodic solutions for hemivariational inequalities. Nonlinear Analysis: Theory, Methods & Applications 2008,68(4):747-767. 10.1016/j.na.2006.11.032
Jankowski T: Ordinary differential equations with nonlinear boundary conditions of antiperiodic type. Computers & Mathematics with Applications 2004,47(8-9):1419-1428. 10.1016/S0898-1221(04)90134-4
Aftabizadeh AR, Aizicovici S, Pavel NH: Anti-periodic boundary value problems for higher order differential equations in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 1992,18(3):253-267. 10.1016/0362-546X(92)90063-K
Aizicovici S, McKibben M, Reich S: Anti-periodic solutions to nonmonotone evolution equations with discontinuous nonlinearities. Nonlinear Analysis: Theory, Methods & Applications 2001,43(2):233-251. 10.1016/S0362-546X(99)00192-3
Aizicovici S, Pavel NH: Anti-periodic solutions to a class of nonlinear differential equations in Hilbert space. Journal of Functional Analysis 1991,99(2):387-408. 10.1016/0022-1236(91)90046-8
Cabada A, Vivero DR: Existence and uniqueness of solutions of higher-order antiperiodic dynamic equations. Advances in Difference Equations 2004,2004(4):291-310. 10.1155/S1687183904310022
Wang K: A new existence result for nonlinear first-order anti-periodic boundary value problems. Applied Mathematics Letters 2008,21(11):1149-1154. 10.1016/j.aml.2007.12.013
Wang K, Li Y: A note on existence of (anti-)periodic and heteroclinic solutions for a class of second-order odes. Nonlinear Analysis: Theory, Methods & Applications. 2009,70(4):1711-1724. 10.1016/j.na.2008.02.054
Wang W, Shen J: Existence of solutions for anti-periodic boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2009,70(2):598-605. 10.1016/j.na.2007.12.031
Nieto JJ, Tisdell CC: Existence and uniqueness of solutions to first-order systems of nonlinear impulsive boundary-value problems with sub-, super-linear or linear growth. Electronic Journal of Differential Equations 2007,2007(105):1-14.
Chen Y, Nieto JJ, O'Regan D: Anti-periodic solutions for fully nonlinear first-order differential equations. Mathematical and Computer Modelling 2007,46(9-10):1183-1190. 10.1016/j.mcm.2006.12.006
Ding W, Xing Y, Han M: Anti-periodic boundary value problems for first order impulsive functional differential equations. Applied Mathematics and Computation 2007,186(1):45-53. 10.1016/j.amc.2006.07.087
Luo Z, Shen J, Nieto JJ: Antiperiodic boundary value problem for first-order impulsive ordinary differential equations. Computers & Mathematics with Applications 2005,49(2-3):253-261. 10.1016/j.camwa.2004.08.010
Cabada A, Liz E, Lois S: Green's function and maximum principle for higher order ordinary differential equations with impulses. The Rocky Mountain Journal of Mathematics 2000,30(2):435-446. 10.1216/rmjm/1022009274
Chen J, Tisdell CC, Yuan R: On the solvability of periodic boundary value problems with impulse. Journal of Mathematical Analysis and Applications 2007,331(2):902-912. 10.1016/j.jmaa.2006.09.021
Rudd M, Tisdell CC: On the solvability of two-point, second-order boundary value problems. Applied Mathematics Letters 2007,20(7):824-828. 10.1016/j.aml.2006.08.028
Acknowledgments
This research is supported by Ad Futura Scientific and Educational Foundation of the Republic of Slovenia, the Ministry of Higher Education, Science and Technology of the Republic of Slovenia; the Nova Kreditna Banka Maribor; TELEKOM Slovenije; National Natural Science Foundation of China (10671127); National Natural Science Foundation of Shanghai (08ZR1416000); and Foundation of Science and Technology Commission of Shanghai Municipality (06XD14034).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xing, Y., Romanovski, V. On the Solvability of Second-Order Impulsive Differential Equations with Antiperiodic Boundary Value Conditions. Bound Value Probl 2008, 864297 (2008). https://doi.org/10.1155/2008/864297
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/864297
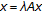 has a solution for
has a solution for 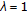 , or
, or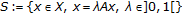 is unbounded.
is unbounded.